Investigation 1.5: Buttered Side Down Again?

Section 3.5 Investigation 1.5: Buttered Side Down Again?

So far, we have looked for evidence in favor of a "greater than" or "less than" alternative hypothesis. But what if our research question is interested in either type of outcome?

🔗

Exercises 3.5.1 The Study

The folks at MythBusters, a popular television program on the Discovery Channel, wanted to investigate whether a piece of toast that has been buttered on one side is more likely to land butter/messy side down or butter-side up. First, they wanted to design a toast-dropping rig that would have no built-in bias for unbuttered toast to land on either side when dropped. For this pilot study, they labeled the sides "top" and "bottom" for ten unbuttered pieces of toast and counted how many landed "top-down."

🔗

1. Define Process and Variable.

Identify the sample/random process and variable of interest in this study. Which outcome will you consider "success"? Do we have a binomial process?

🔗

Hint.

Consider what is being repeated and what outcome is measured each time.

🔗

Solution.

Random process: Repeated dropping pieces of toast, assuming identical conditions.

🔗

Variable: Whether the piece of toast lands top side down or top side up

🔗

Success: Top side down

🔗

Binomial process: Yes, assuming each drop is independent with the same probability.

🔗

2. Define Parameter.

Identify the parameter of interest in this study (in words).

🔗

Hint.

What long-run proportion are we interested in?

🔗

Solution.

The probability of a piece of toast landing top side down.

🔗

3. Parameter Symbol.

What symbol should we use to represent this parameter?

🔗

Hint.

Look for the Greek letter used for a process probability in a binomial distribution.

🔗

\(\hat{p}\)
This is the symbol for the sample proportion (statistic), not the population parameter.
\(\pi\)
Correct! We use \(\pi\) to represent the probability of success in a binomial process.
\(\mu\)
This is the symbol for a population mean, not a probability.
\(p\)
While p is sometimes used for probability, we use the Greek letter \(\pi\) for the process probability parameter.

Solution.

We use \(\pi\) to represent the probability of a piece of toast landing top side down.

🔗

4. State Null Hypothesis.

State the null hypothesis using symbols and words.

🔗

\(H_0\text{:}\)

🔗

Hint.

If there’s no bias, what should the probability be?

🔗

Solution.

\(H_0: \pi = 0.5\) (equally likely to land top down or top up)

🔗

5. Two-Sided Alternative.

With 10 pieces of toast, what outcomes for the number of successes would convince you that there was a problem with the rig? Suggest a way of stating the alternative hypothesis that reflects this interest/prior suspicion.

🔗

\(H_a\text{:}\)

🔗

Hint.

Would you be concerned if the result was extreme in either direction (too many or too few successes)?

🔗

Solution.

\(H_a: \pi \neq 0.50\) (one side is more likely)

🔗

This is a two-sided alternative hypothesis.

🔗

You have now stated a two-sided alternative hypothesis (rather than a "one-sided" alternative of strictly less than or strictly greater than). So now we need to decide which values we will consider "or more extreme" in calculating the p-value.

🔗

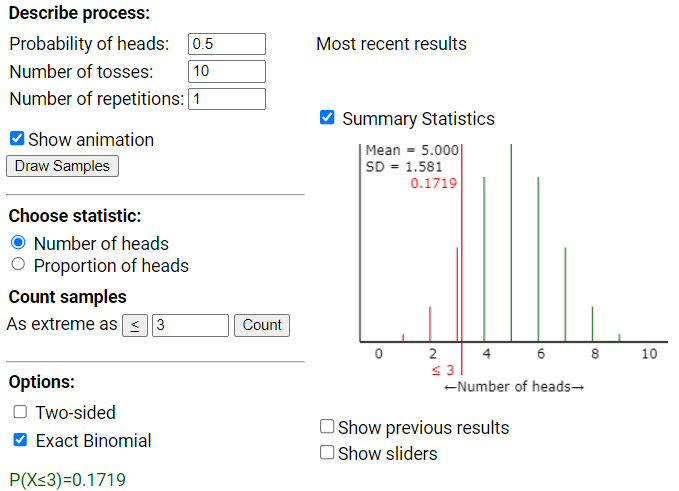
In this pilot study, the toast landed top-down 3 times and top-up 7 times. Use the One Proportion Inference applet to calculate the binomial probability of 3 or fewer successes in 10 attempts, assuming the null hypothesis is true (i.e., P(X ≤ 3) where X is the number landing top-down).

🔗

6. Calculate One-Sided Probability.

Report the one-sided p-value:

🔗

Hint.

Use technology with \(n = 10, π = 0.5\text{,}\) and find \(P(X ≤ 3)\text{.}\)

🔗

Solution.

P(X ≤ 3) = 0.1719

🔗

Binomial distribution for n=10, pi=0.5 showing P(X less than or equal to 3)

🔗

7. Identify More Extreme Outcomes.

Conjecture: What other outcomes would you consider "as or more surprising" as 3 or fewer successes?

🔗

Hint.

Think about the symmetry of the distribution when π = 0.5.

🔗

Solution.

Reasonable conjectures include X ≥ 7

🔗

8. Calculate Two-Sided p-value.

If we calculate the two-sided p-value as P(X ≤ 3) + P(X ≥ 7), what would you report for the p-value? Would you find this p-value to be convincing evidence in favor of the two-sided alternative hypothesis?

🔗

Hint.

When the distribution is symmetric, P(X ≥ 7) = P(X ≤ 3).

🔗

Solution.

The applet tells us P(X ≥ 7) also equals 0.1719, so the two-sided p-value = 2(0.1719) = 0.3438

🔗

This p-value is quite large, so we would not have convincing evidence against the null hypothesis.

🔗

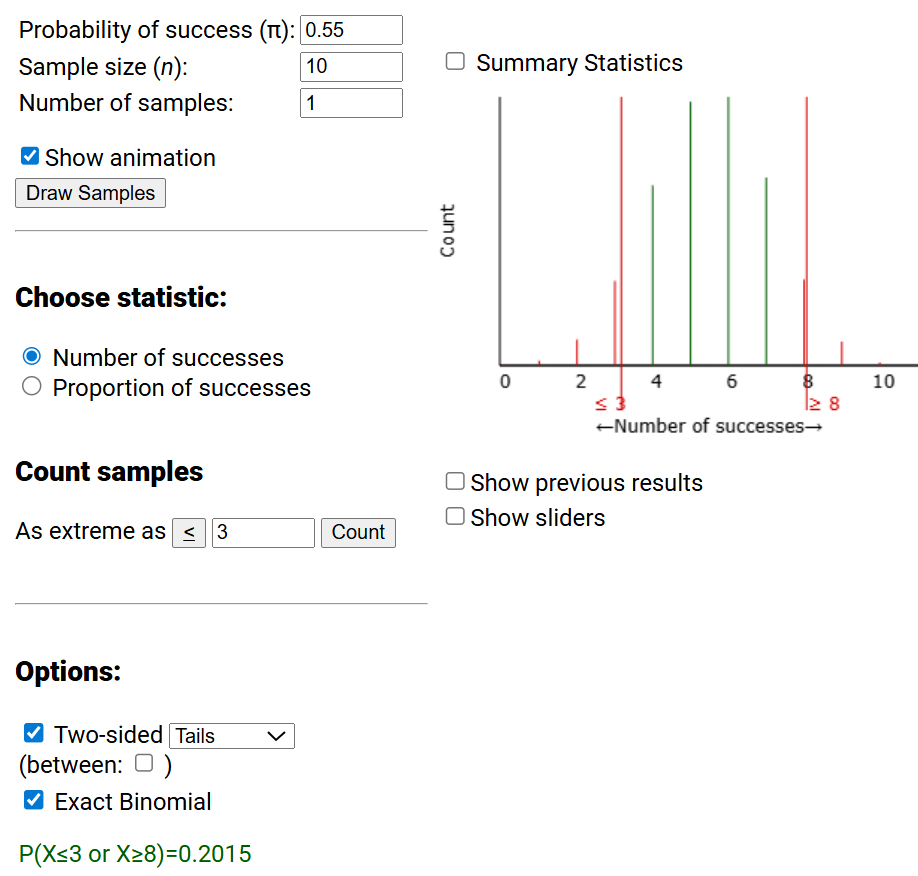
What if our original hypotheses had been \(H_0: \pi = 0.55\) vs. \(H_a: \pi \neq 0.55\text{?}\)

9. Alternative Null Hypothesis.

Restate the alternative hypothesis in words.

🔗

How will the null distribution change?

🔗

Hint.

How does changing π from 0.5 to 0.55 affect the center of the distribution?

🔗

Solution.

Alternative hypothesis in words: Now we think the long-run proportion of toast drops landing top side down is not 0.55.

🔗

How the null distribution changes: This will shift the null distribution to center at 5.5 rather than at 5 successes.

🔗

10. Left Tail Probability.

Make this change in the applet and find the binomial probability of 3 or fewer successes:

🔗

Hint.

Use \(n = 10, π = 0.55\text{,}\) and find \(P(X ≤ 3)\text{.}\)

🔗

Solution.

\(P(X ≤ 3\) when \(π = 0.55) = 0.1020\)

🔗

11. Right Tail Comparison.

Now find P(X ≥ 7) when π = 0.55. How does it compare to P(X ≤ 3)? Why does this make sense?

🔗

Hint.

Is 7 further from the expected value than 3 is?

🔗

Solution.

P(X ≥ 7) increases to 0.2660 because now an outcome of 7 is closer to the expected value of the null distribution.

🔗

In this text, we will consider outcomes "more extreme" than the observed outcome if the "tail probability" is less than or equal to the tail probability of the observed outcome. So for this null hypothesis (π = 0.55), because P(X ≥ 7) > P(X ≤ 3), we would not consider x = 7 to be "more extreme" than x = 3. Therefore, we would not include x = 7 in the p-value calculation. Notice, this distinction arose once our binomial distribution was not symmetric (π ≠ 0.50).

🔗

12. Find More Extreme Value.

Find P(X ≥ 8):

🔗

Is x = 8 considered more extreme than x = 3?

🔗

Hint.

Compare P(X ≥ 8) to P(X ≤ 3) = 0.1020.

🔗

Solution.

P(X ≥ 8) = 0.0996 which is now smaller than P(X ≤ 3) so we could consider x = 8 a more extreme observation compared to x = 3.

🔗

13. Two-Sided p-value for π = 0.55.

Calculate the two-sided p-value as P(X ≤ 3) + P(X ≥ 8):

🔗

Hint.

Add the two tail probabilities you found.

🔗

Solution.

0.1020 + 0.0996 = 0.2016

🔗

14. Verify with Applet.

Verify your result in the applet: Start with 3 and use the "Tails" option, then check the Two-sided box.

🔗

Hint.

Use the "Tails" option in the pull-down menu.

🔗

Verified
Correct! Results match if you start with P(X ≤ 3) and use the pull-down menu to select "Tails" for the two-sided p-value.
Not Verified
Check again. Results should match if you start with P(X ≤ 3) and use the pull-down menu to select "Tails" for the two-sided p-value.

Solution.

Two-sided binomial test for n=10, pi=0.55 showing two-sided p-value

🔗

There are other ways to define "more extreme" as well, and results will vary across different software packages (see Practice Problem 1.5). But the results will be more similar the more symmetric the null distribution is, and when the null distribution is skewed, adjusting for the asymmetry is generally preferred to going "the same distance" on each side or doubling the one-sided p-value.

🔗

Definition: Two-sided p-values.

Two-sided p-values are used with two-sided alternative hypotheses (≠, not equal to). A two-sided p-value considers outcomes in both tails that are at least as rare as the observed result, where at least as rare could be defined as having a smaller tail probability of occurring as the observed statistic. If the null distribution is symmetric, the approaches are equivalent and the two-sided p-value will be double the one-sided p-value.

🔗

15. Evaluate Pilot Study Conclusion.

The MythBusters decided a 3/7 split was "way outside a random sample" and so they needed to build a different toast-dropping rig. Do you agree with their conclusion from the pilot study? Write a short paragraph to the MythBusters justifying your answer. Include appropriate numerical evidence to support your argument.

🔗

Hint.

Consider both p-values you calculated (for π=0.50 and π=0.55).

🔗

Solution.

Based on the two-sided p-values, both 0.50 and 0.55 are plausible values for the probability of a piece of toast landing top side down. Because 0.50 is plausible (p-value = 0.3438), these data do not provide convincing evidence that there is a built-in bias with the mechanism and they could have continued to use it.

🔗

After building a new rig (that they were more confident had no bias), they used the rig to drop buttered toast from the roof of a building. The Mythbusters weren’t sure whether the toast would land butter-side down (as in the myth) or whether, like a curved leaf falling from a tree, the toast might try to "right itself" and land with the indented side (from being buttered) down. So again, they wanted to use a two-sided alternative hypothesis, allowing for either possibility to be of interest.

🔗

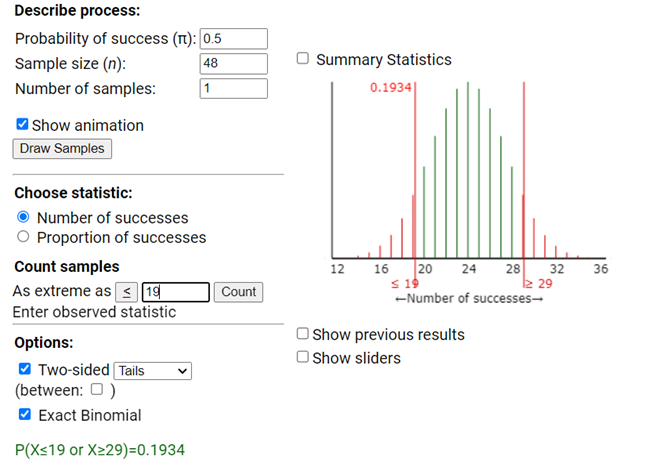
They dropped 48 pieces of toast, with 19 landing butter-side-down.

🔗

16. Buttered Toast Two-Sided Test.

Use the applet to find the two-sided p-value for testing \(H_0: \pi = 0.5\) vs. \(H_a: \pi \neq 0.50\text{.}\) Do you have strong enough evidence to reject the null hypothesis and conclude π differs from 0.5? Why are you making this decision?

🔗

Aside: One Proportion Inference applet.

Hint.

Use n=48, observed=19, π=0.5, and check the two-sided box.

🔗

Solution.

Two-sided binomial test for n=48, pi=0.5, observed=19

The p-value is not small (p-value = 0.1934, which is larger than 0.05), so we fail to reject the null hypothesis that π = 0.50. We conclude it is plausible that buttered toast is equally likely to land up or down when dropped from the top of a building.

🔗

Study Conclusions.

These data (19 out of 48) do not provide convincing evidence against the null hypothesis that toast buttered on one side is equally likely to land butter side up or down (two-sided p-value = 0.1934). In other words, it is plausible that this is a 50/50 process. However, this analysis cannot be used as proof that π = 0.50, as other values could be plausible as well. The sample data allow for many (technically, infinitely many) plausible values of this probability, as you will explore in the next investigation.

🔗

Discussion.

Recall that the process we are using to test our hypotheses is to first assume the null hypothesis is true. For this reason, we can never use this process as evidence for the null hypothesis, only lack of evidence against it. Keep in mind the saying "Absence of evidence is not evidence of absence." Also, note that our evidence depends on the form of the alternative hypothesis. A more complete statement is that we do not have evidence in favor of the alternative that we specified, and that our strength of evidence could differ if we started with a different alternative hypothesis.

🔗

Technology Detour – Two-sided p-values.

17. Calculate Two-Sided p-values with Technology.

Use technology (R or JMP) to calculate the two-sided p-value for the buttered toast study (19 successes in 48 trials with probability 0.5). Choose one set of instructions below by clicking on a hint.

🔗

Two-sided p-value = (four decimal places)

🔗

Hint 1. Applet Instructions

In the One Proportion Inference applet:

🔗

Check the two-sided box
🔗

🔗
For the "smallest tail probability" approach, set the pull-down menu to "Tails" (finds tail value on other side that is first below the one-sided p-value)
🔗

🔗
For the "smallest p-value" approach, set the pull-down menu to "Individual" (sums all probabilities smaller than the observed)
🔗

🔗
(These will match when the distribution is symmetric.)
🔗

🔗

🔗

Hint 2. R Instructions

Using the iscambinomtest function, specify alternative = "two.sided"

🔗

(Smallest p-value method)

🔗

The output will show:

🔗

The observed number of successes (19) and sample size (48)
🔗

🔗
The hypothesized probability (0.5)
🔗

🔗
The two-sided p-value: 0.1934
🔗

🔗
A graph showing the binomial distribution with both tails shaded
🔗

🔗

🔗

Hint 3. JMP Instructions

Note: The default two-sided test under Analyze > Distribution is not an "exact" binomial test.

🔗

Use radio button to create JMP two-sided binomial test output

🔗

Solution.

The two-sided p-value is 0.1934. The output table will show the two-sided p-value for the exact binomial test. For the buttered toast example with 19 successes out of 48 trials and hypothesized probability of 0.5, the two-sided p-value should be approximately 0.1934.

🔗

Subsection 3.5.2 Practice Problem 1.5

There are other approaches for calculating the two-sided p-value. For example, we could consider an outcome \(k\) more extreme than the observed, if \(P(X = k) < P(X = observed)\text{.}\)

🔗

Checkpoint 3.5.5. Explain Alternative Approach.

Explain the distinction in this approach and the one used above.

🔗

Checkpoint 3.5.6. Apply Alternative Method.

Return to the pilot study with 3 successes out of n = 10 drops. Based on this new approach, which values above 5 would you consider more extreme than 3 when \(\pi\) = 0.55? Document your justification. What is the resulting two-sided p-value?

🔗

Hint.

As extreme as =

🔗

Checkpoint 3.5.7. Strange Behavior with Extreme Observations.

Suppose n = 20 and you observed 0 successes. Find the two-sided p-values using the approach suggested in the previous question for π = 0.13, π = 0.145, and π = 0.15. According to the two-sided p-values, which of these values are plausible for π at the 10% level of significance? What strange behavior do you observe?

🔗

Checkpoint 3.5.8. Why Not Other Methods?

Or we could choose to use x values that are the same number (or more) of standard deviations above the mean or double the one-sided p-value. Why do you think these methods are not recommended in general?

🔗

Checkpoint 3.5.9. When to Use One-Sided Tests.

It’s interesting that the one-sided p-value for the pilot study is also not statistically significant. If it had been, would it be reasonable for the Mythbusters to use the one-sided p-value instead to support their conclusion? Explain.

🔗

You have attempted of activities on this page.

🔗

Prev Top Next