Section 7.1 Sample in a Jar

Sampling distributions are the conceptual key to statistical inference. Many approaches to understanding sampling distributions use examples of drawing marbles or gumballs from a large jar to illustrate the influences of randomness on sampling. Using the list of U.S. states illustrates how a non-normal distribution nonetheless has a normal sampling distribution of means.
Imagine a gum ball jar full of gumballs of two different colors, red and blue. The jar was filled from a source that provided 100 red gum balls and 100 blue gum balls, but when these were poured into the jar they got all mixed up. If you drew eight gumballs from the jar at random, what colors would you get? If things worked out perfectly, which they never do, you would get four red and four blue. This is half and half, the same ratio of red and blue that is in the jar as a whole. Of course, it rarely works out this way, does it? Instead of getting four red and four blue you might get three red and five blue or any other mix you can think of. In fact, it would be possible, though perhaps not likely, to get eight red gumballs. The basic situation, though, is that we really don’t know what mix of red and blue we will get with one draw of eight gumballs. That’s uncertainty for you, the forces of randomness affecting our sample of eight gumballs in unpredictable ways.
Here’s an interesting idea, though, that is no help at all in predicting what will happen in any one sample, but is great at showing what will occur in the long run. Pull eight gumballs from the jar, count the number of red ones and then throw them back. We do not have to count the number of blue because 8 = #red + #blue. Mix up the jar again and then draw eight more gumballs and count the number of red. Keep doing this many times. Here’s an example of what you might get:
| DRAW | #RED |
|---|---|
| 1 | 5 |
| 2 | 3 |
| 3 | 6 |
| 4 | 2 |
Notice that the left column is just counting up the number of sample draws we have done. The right column is the interesting one because it is the count of the number of red gumballs in each particular sample draw. In this example, things are all over the place. In sample draw 4 we only have two red gumballs, but in sample draw 3 we have 6 red gumballs. But the most interesting part of this example is that if you average the number of red gumballs over all of the draws, the average comes out to exactly four red gumballs per draw, which is what we would expect in a jar that is half and half. Now this is a contrived example and we won’t always get such a perfect result so quickly, but if you did four thousand draws instead of four, you would get pretty close to the perfect result.
This process of repeatedly drawing a subset from a "population" is called "Sampling," and the end result of doing lots of sampling is a Sampling Distribution. Note that we are using the word population in the previous sentence in its statistical sense to refer to the totality of units from which a sample can be drawn. It is just a coincidence that our dataset contains the number of people in each state and that this value is also referred to as "population." Next we will get R to help us draw lots of samples from our U.S. state dataset.
Conveniently, R has a function called sample(), that will draw a random sample from a data set with just a single call. We can try it now with our state data:
read_excel() function when the Excel file has no column names in the first row and you set col_names = FALSE. It assigns default column names like ...1, ...2, etc., and tells you that it renamed them — that’s what the "New names" message means.As a matter of practice, note that we called the sample() function with three arguments. The first argument was the data source. For the second and third arguments, rather than rely on the order in which we specify the arguments, we have used "named arguments" to make sure that R does what we wanted. The size=16 argument asks R to draw a sample of 16 state data values. The replace=TRUE argument specifies a style of sampling which statisticians use very often to simplify the mathematics of their proofs. For us, sampling with or without replacement does not usually have any practical effects, so we will just go with what the statisticians typically do.
When we’re working with numbers such as these state values, instead of counting gumball colors, we’re more interested in finding out the average, or what you now know as the mean. So we could also ask R to calculate a mean() of the sample for us:
There’s the nested function call again. The output no longer shows the 16 values that R has sampled from the list of 51. Instead it used those 16 values to calculate the mean and display that for us. If you have a good memory, or merely took the time to look in the last chapter, you will remember that the actual mean of our 51 observations is 6,053,834. So the mean that we got from this one sample of 16 states is really not even close to the true mean value of our 51 observations. Are we worried? Definitely not! We know that when we draw a sample, whether it is gumballs or states, we will never hit the true population mean right on the head. We’re interested not in any one sample, but in what happens over the long haul. So now we’ve got to get R to repeat this process for us, not once, not four times, but four hundred times or four thousand times. Like most programming languages, R has a variety of ways of repeating an activity. One of the easiest ones to use is the replicate() function. To start, let’s just try four replications:
Couldn’t be any easier. We took the exact same command as before, which was a nested function to calculate the mean() of a random sample of 16 states (shown above in bold). This time, we put that command inside the replicate() function so we could run it over and over again. The simplify=TRUE argument asks R to return the results as a simple vector of means, perfect for what we are trying to do. We only ran it four times, so that we would not have a big screen full of numbers. From here, though, it is easy to ramp up to repeating the process four hundred times. You can try that and see the output, but for here in the book we will encapsulate the whole replicate function inside another mean(), so that we can get the average of all 400 of the sample means. Here we go:
In the command above, the outermost mean()command is bolded to show what is different from the previous command. So, put into
that words, this deeply nested command accomplishes the following: a) Draw 400 samples of size n=8 from our full data set of 51 states; b)
Calculate the mean from each sample and keep it in a list; c) When finished with the list of 400 of these means, calculate the mean of that list of means. You can see that the mean of four hundred sample means is 5,958,336. Now that is still not the exact value of the whole data set, but it is getting close. We’re off by about 95,000, which is roughly an error of about 1.6% (more precisely, 95,498/ 6,053,834 = 1.58%. You may have also noticed that it took a little while to run that command, even if you have a fast computer. There’s a lot of work going on there! Let’s push it a bit further and see if we can get closer to the true mean for all of our data:
Now we are even closer! We are now less than 1% away from the true population mean value. Note that the results you get may be a bit different, because when you run the commands, each of the 400 or 4000 samples that is drawn will be slightly different than the ones that were drawn for the commands above. What will not be much different is the overall level of accuracy.
We’re ready to take the next step. Instead of summarizing our whole sampling distribution in a single average, let’s look at the distribution of means using a histogram.
The histogram displays the complete list of 4000 means as frequencies. Take a close look so that you can get more practice reading frequency histograms. This one shows a very typical configuration that is almost bell-shaped, but still has a bit of "skewness" off to the right.The tallest, and therefore most frequent range of values is right near the true mean of 6,053,834.
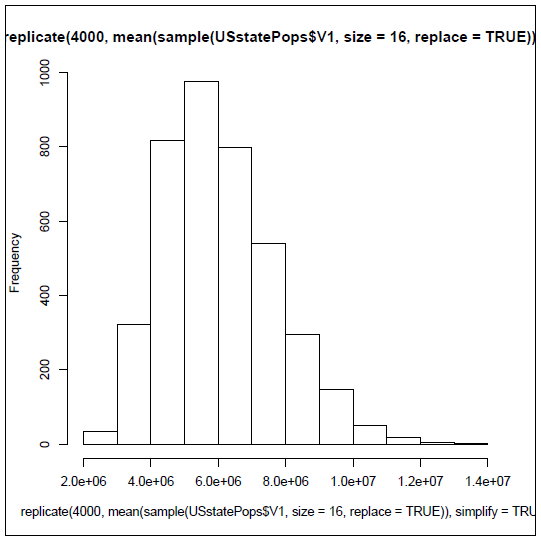
By the way, were you able to figure out the command to generate this histogram on your own? All you had to do was substitute hist() for the outermost mean() in the previous command. In case you struggled, here it is:
You have attempted of activities on this page.
