Introduction to Data Science Using R Runestone Version 1

In order to understand the following code, you will probably need to know what the cat() function does. In R, the cat() function (short for "concatenate") is primarily used to display output directly to the console or to a file. Unlike print(), cat() is designed for producing more human-readable output by concatenating its arguments and printing them sequentially. By default, it separates arguments with a space, and you can explicitly add newline characters (\n) to control line breaks.

Now we’re ready to have some fun with a good sized list of numbers. Here are the basic descriptive statistics on the population of the states:

Some great summary information there, but wait, a couple things have gone awry:

Other than these two issues, we now know that the average population of a U.S. state is 6,053,834 with a standard deviation of 6,823,984. You may be wondering, though, what does it mean to have a standard deviation of almost seven million? The mean and standard deviation are OK, and they certainly are mighty precise, but for most of us, it would make much more sense to have a picture that shows the central tendency and the dispersion of a large set of numbers. So here we go. Run this command:

hist(USstatePops$...1)

Here’s the output you should get:

A histogram is a specialized type of bar graph designed to show "frequencies." Frequencies means how often a particular value or range of values occurs in a dataset. This histogram shows a very interesting picture. There are nearly 30 states with populations under five million, another 10 states with populations under 10 million, and then a very small number of states with populations greater than 10 million. Having said all that, how do we glean this kind of information from the graph? First, look along the Y-axis (the vertical axis on the left) for an indication of how often the data occur. The tallest bar is just to the right of this and it is nearly up to the 30 mark. To know what this tall bar represents, look along the X-axis (the horizontal axis at the bottom) and see that there is a tick mark for every two bars. We see scientific notation under each tick mark. The first tick mark is 1e+07, which translates to 10,000,000. So each new bar (or an empty space where a bar would go) goes up by five million in population. With these points in mind it should now be easy to see that there are nearly 30 states with populations under five million.

If you think about presidential elections, or the locations of schools and businesses, or how a single U.S. state might compare with other countries in the world, it is interesting to know that there are two really giant states and then lots of much smaller states. Once you have some practice reading histograms, all of the knowledge is available at a glance.

On the other hand there is something unsatisfying about this diagram. With over forty of the states clustered into the first couple of bars, there might be some more details hiding in there that we would like to know about. This concern translates into the number of bars shown in the histogram. There are eight shown here, so why did R pick eight?

The answer is that the hist() function has an algorithm or recipe for deciding on the number of categories/bars to use by default. The number of observations and the spread of the data and the amount of empty space there would be are all taken into account. Fortunately it is possible and easy to ask R to use more or fewer categories/bars with the "breaks" parameter, like this:

hist(USstatePops$...1, breaks=20)

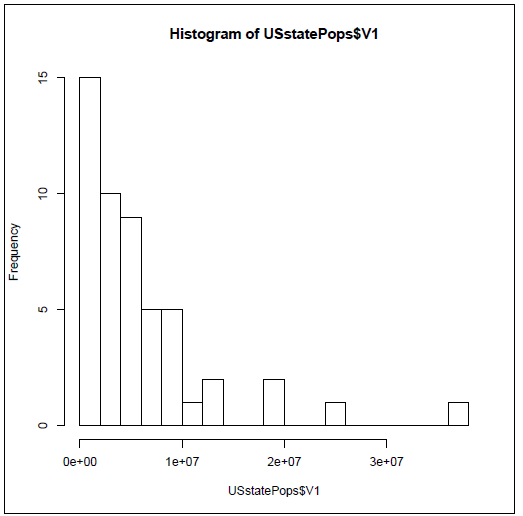
Histogram of USstatePops$...1

This gives us five bars per tick mark or about two million for each bar. So the new histogram above shows very much the same pattern as before: 15 states with populations under two million. The pattern that you see here is referred to as a distribution. This is a distribution that starts off tall on the left and swoops downward quickly as it moves to the right. You might call this a "reverse-J" distribution because it looks a little like the shape a J makes, although flipped around vertically. More technically this could be referred to as a Pareto distribution (named after the economist Vilfredo Pareto). We don’t have to worry about why it may be a Pareto distribution at this stage, but we can speculate on why the distribution looks the way it does. First, you can’t have a state with no people in it, or worse yet negative population. It just doesn’t make any sense. So a state has to have at least a few people in it, and if you look through U.S. history every state began as a colony or a territory that had at least a few people in it. On the other hand, what does it take to grow really large in population? You need a lot of land, first of all, and then a good reason for lots of people to move there or lots of people to be born there. So there are lots of limits to growth: Rhode Island is too small to have a bazillion people in it and Alaska, although it has tons of land, is too cold for lots of people to want to move there. So all states probably started small and grew, but it is really difficult to grow really huge. As a result we have a distribution where most of the cases are clustered near the bottom of the scale and just a few push up higher and higher. But as you go higher, there are fewer and fewer states that can get that big, and by the time you are out at the end, just shy of 40 million people, there’s only one state that has managed to get that big. By the way, do you know or can you guess what that humongous state is?