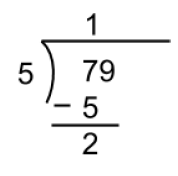Group Work - Remainder Operator (%)

Section 2.19 Group Work - Remainder Operator (%)

It is best to use a POGIL approach with the following. In POGIL students work in groups on activities and each member has an assigned role. For more information see https://cspogil.org/Home

https://cspogil.org/Home

. This page is based on a POGIL activity from Helen Hu at that site.

🔗

Look at the expressions in the code above and the output. Then answer the following questions.

🔗

Activity 2.19.1.

Run the following code to see what it prints.

🔗

Activity 2.19.2.

🔗

Activity 2.19.3.

🔗

Subsection 2.19.1 Going Beyond Remainder 4

Activity 2.19.4.

🔗

Activity 2.19.5.

🔗

Subsection 2.19.2 Look Deeper

Activity 2.19.6.

Look at the code above for the numbers such that n % 4 returns 1. How do these numbers differ from the ones that return zero?

🔗

Subsection 2.19.3 More Practice

Subsection 2.19.4 Long Division with a Remainder

Consider how you did long division in elementary school where you determined what number goes evenly into another number and the remainder.

🔗

Activity 2.19.11.

🔗

Subsection 2.19.5 Dividing Evenly

Imagine if you were given candies to evenly divide amoung members of a group of four people. Follow kindergarten rules where every group member gets the same number of candies and the extras go back to the teacher.

🔗