DS Search Tree Implementation

Section 8.4 Search Tree Implementation

A binary search tree (BST) relies on the property that keys that are less than the parent are found in the left subtree, and keys that are greater than the parent are found in the right subtree. We will call this the BST property. As we implement the ComparableMapADT interface as described above, the BST property will guide our implementation. Figure 8.4.1 illustrates this property of a binary search tree, showing the keys without any associated values. Notice that the property holds for each parent and child. All of the keys in the left subtree are less than the key in the root. All of the keys in the right subtree are greater than the root.

🔗

Figure 8.4.1. A Simple Binary Search Tree
🔗

Subsection 8.4.1 Constructing a Binary Search Tree

Now that you know what a binary search tree is, we will look at how a binary search tree is constructed. The search tree in Figure 8.4.1 represents the nodes that exist after we have inserted the following keys in the order shown: \(70, 31, 93, 94, 14, 23, 73\text{.}\) Since 70 was the first key inserted into the tree, it is the root. Next, 31 is less than 70, so it becomes the left child of 70. Next, 93 is greater than 70, so it becomes the right child of 70. Now we have two levels of the tree filled, so the next key is going to be the left or right child of either 31 or 93. Since 94 is greater than 70 and 93, it becomes the right child of 93. Similarly 14 is less than 70 and 31, so it becomes the left child of 31. 23 is also less than 31, so it must be in the left subtree of 31. However, it is greater than 14, so it becomes the right child of 14.

🔗

To implement the binary search tree, we will use the nodes and references approach similar to the one we used to implement the linked list and the expression tree. However, because we must be able create and work with a binary search tree that is empty, our implementation will use two classes. The first class we will call BSTMap, and the second class we will call TreeNode. The BSTMap class has a reference to the TreeNode that is the root of the binary search tree. Within the BSTMap class, there are a collection of both private and public methods. In most cases the public methods first check to see if the tree is empty. If there are nodes in the tree, the request is passed on to a private method that takes the root as a parameter. In the case where the tree is empty or we want to delete the key at the root of the tree, we must take special action. The code for the beginning of the BSTMap class is shown in Listing 8.4.2.

🔗

Listing 8.4.2. Start of BSTMap class

🔗

class BSTMap<K : Comparable<K>, V> : ComparableMapADT<K, V> {

    var root: TreeNode? = null
    var nodeCount = 0

    override fun size(): Int {
        return nodeCount
    }

    // More code follows
}

The TreeNode class provides many helper methods that make the work done in the BSTMap class methods much easier. The start for the TreeNode class, along with these helper methods, is shown in Listing 8.4.3. We will put this class definition inside the BinarySearchTree class, and declare it as an inner class. This will automatically give a TreeNode access to all the BinarySearchTree properties, including the generic types K and V. As you can see in the listing, many of these helper methods help to classify a node according to its own position as a child (left or right) and the kind of children the node has. The TreeNode class will also explicitly keep track of the parent as an attribute of each node. You will see why this is important when we discuss the implementation for the remove method in Subsection 8.4.5.

🔗

On lines 4 – 6, we have added default values of null for each of the attributes shown. Sometimes, we want to construct a TreeNode without only some of the information, so the default values can fill in the remaining values for us.

🔗

Listing 8.4.3. Start of TreeNode class.

🔗

inner class TreeNode(
       var key: K,
       var value: V,
       var parent: TreeNode? = null,
       var leftChild: TreeNode? = null,
       var rightChild: TreeNode? = null
   ) {
       
       // Is this node a left child of a parent?
       fun isLeftChild(): Boolean {
           val parent = parent  // Local copy of parent for null safety
           return parent != null && parent.leftChild == this
       }

       // Is this node a right child of a parent?
       fun isRightChild(): Boolean {
           val parent = parent   // Local copy of parent for null safety
           return parent != null && parent.rightChild == this
       }

       // Is this a leaf node? (Leaf nodes have no children)
       fun isLeaf(): Boolean {
           return (leftChild == null && rightChild == null)
       }

       fun replaceValue(key: K, value: V, left: TreeNode?, right: TreeNode?) {
           this.key = key
           this.value = value
           this.leftChild = left
           this.rightChild = right
           this.leftChild?.parent = this
           this.rightChild?.parent = this
       }

       override fun toString(): String {
           return "key: " + key + " value: " + value + "\n  " +
                   " left: " + leftChild + " right: " + rightChild +
                   "parent: " + parent
       }
   }

🔗

Subsection 8.4.2 Inserting Keys and Values into a Binary Search Tree

Now that we have the BSTMap shell and the TreeNode, it is time to write the put method that will allow us to build our binary search tree. The put method is a method of the BSTMap class. This method will check to see if the tree already has a root. If there is not a root, then put will create a new TreeNode and install it as the root of the tree. If a root node is already in place, then put calls the private recursive helper method put (with three parameters) to search the tree according to the following algorithm:

🔗

Starting at the root of the tree, search the binary tree comparing the new key to the key in the current node. If the new key is less than the current node, search the left subtree. If the new key is greater than the current node, search the right subtree.
🔗

🔗
When there is no left or right child to search, we have found the position in the tree where the new node should be installed.
🔗

🔗
To add a node to the tree, create a new TreeNode object and insert the object at the point discovered in the previous step.
🔗

🔗

🔗

Listing 8.4.4 shows the code for inserting a new node in the tree. The public put method with two arguments calls the the private put method, which is written recursively following the steps outlined above. Notice that when a new child is inserted into the tree, the currentNode is passed to the new tree as the parent.

🔗

One important problem with our implementation of insertion is that duplicate keys are not handled properly. As our tree is implemented, a duplicate key will create a new node with the same key value in the right subtree of the node having the original key. The result of this is that the node with the new key will never be found during a search. A better way to handle the insertion of a duplicate key is for the value associated with the new key to replace the old value. We leave fixing this bug as an exercise for you.

🔗

Listing 8.4.4. The put Method

🔗

override fun put(key: K, value: V) {
    // Local copy for null safety
    val root = this.root
    if (root != null) {
        put(key, value, root)
    } else {
        this.root = TreeNode(key, value)
    }
    this.nodeCount += 1
}

private fun put(key: K, value: V, currentNode: TreeNode) {
    // Local copies for null safety
    val currentLeftChild = currentNode.leftChild
    val currentRightChild = currentNode.rightChild

    if (key < currentNode.key) {
        if (currentLeftChild != null) {
            put(key, value, currentLeftChild)
        } else {
            currentNode.leftChild = TreeNode(key, value, currentNode)
        }
    } else {
        if (currentRightChild != null) {
            put(key, value, currentRightChild)
        } else {
            currentNode.rightChild = TreeNode(key, value, currentNode)
        }
    }
}

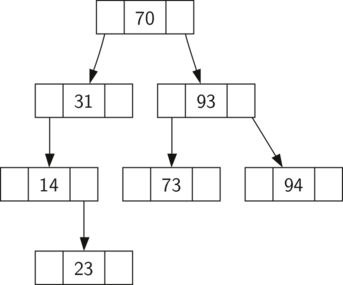
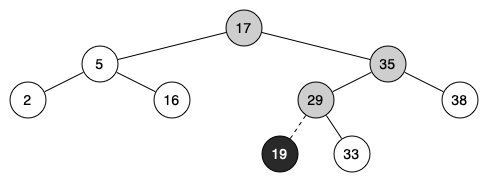
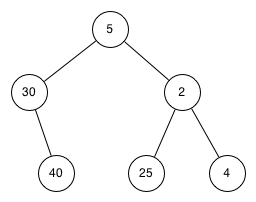
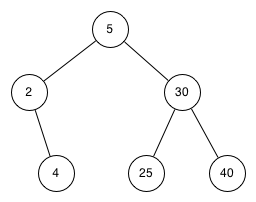
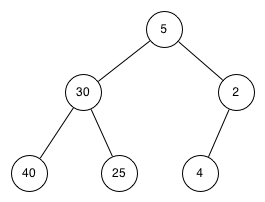
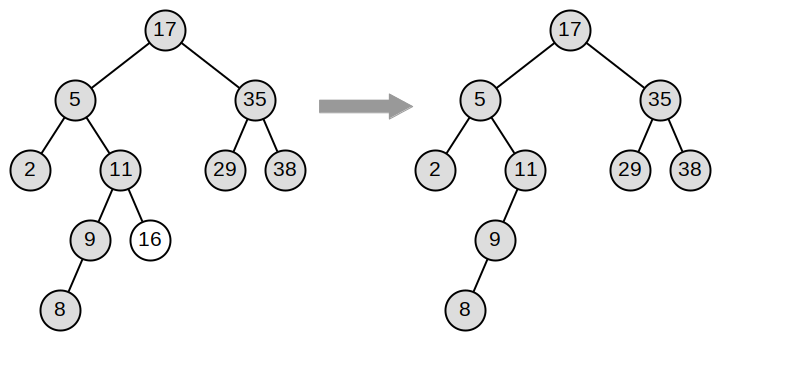
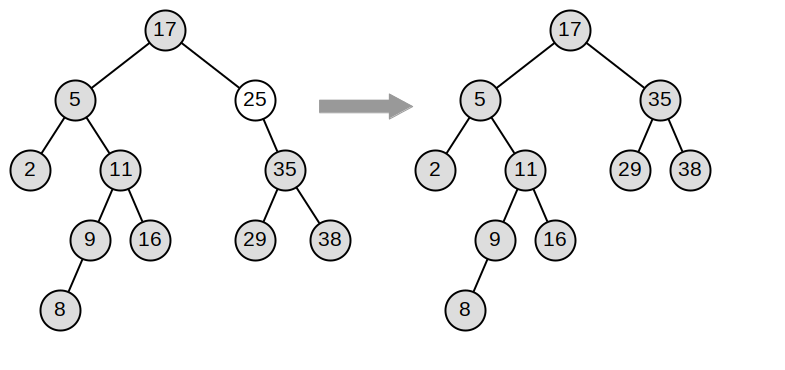
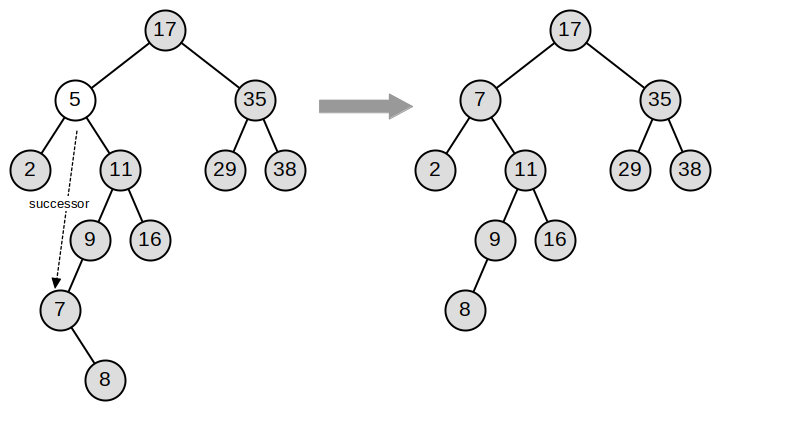
Note 8.4.5. Kotlin Note.

There are two methods named put, but Kotlin does not have a problem with this because they have different method signatures: the method name, the number, and types of arguments. As long as these are different, there is no ambiguity when Kotlin needs to figure out whch method to call. The return type, the access (public or private), and whether or not override is present are not part of the method signature.

🔗

Figure 8.4.6 illustrates the process for inserting a new node into a binary search tree. The lightly shaded nodes indicate the nodes that were visited during the insertion process.

🔗

Figure 8.4.6. Inserting a Node with Key = 19
🔗

Exercises Self Check

1.

Which of the trees shows a correct binary search tree given that the keys were inserted in the following order 5, 30, 2, 40, 25, 4.

🔗

Remember, starting at the root keys less than the root must be in the left subtree, while keys greater than the root go in the right subtree.
good job.
This looks like a binary tree that satisfies the full tree property needed for a heap.

🔗

Subsection 8.4.3 Retrieving Values for a Key in a Binary Search Tree

Once the tree is constructed, the next task is to implement the retrieval of a value for a given key. The get method is less complex than the put method because it searches the tree recursively until it gets to a non-matching leaf node or finds a matching key. When a matching key is found, the value stored in the payload of the node is returned.

🔗

Listing 8.4.7 shows the code for get and the private get helper method. The search code in the helper method uses the same logic for choosing the left or right child as the put helper method. Notice that the get helper method returns a TreeNode to get, which allows the helper method to be used as a flexible method for other BSTMap methods that may need to make use of other data from the TreeNode besides the payload.

🔗

Listing 8.4.7. The get Method

🔗

override fun get(key: K): V? {
    if (this.root != null) {
        val result = get(key, this.root)
        if (result != null) {
            return result.value
        }
    }
    return null
}

fun get(key: K, currentNode: TreeNode?): TreeNode? {
    if (currentNode == null) {
        return null
    }
    if (key == currentNode.key) {
        return currentNode
    } else if (key < currentNode.key) {
        return get(key, currentNode.leftChild)
    } else {
        return get(key, currentNode.rightChild)
    }
}

We can use the get helper method when implementing the containsKey method in Listing 8.4.8; if it returns a node, we return true; if it returns null, we return false:

🔗

Listing 8.4.8. The containsKey Method

🔗

override fun containsKey(key: K): Boolean {
    val result = get(key, this.root)
    return (result != null)
}

🔗

Subsection 8.4.4 Displaying a Binary Search Tree

We would like to be able to see the resulting tree. Rather than display the tree graphically, we will instead display it as a nested list of the format:

🔗

[root [left tree] [right tree]]

Listing 8.4.9 shows the toString method with its stringify helper method, which does an inorder traversal of the tree.

🔗

Listing 8.4.9. Tree to String

🔗

override fun toString(): String {
    return stringify(this.root)
}

fun stringify(node: TreeNode?): String {
    var result = ""
    if (node != null) {
        if (node.isLeaf()) {
            result = " [" + node.key + "]"
        } else {
            result = " [" + node.key + stringify(node.leftChild) +
                    stringify(node.rightChild) + "]"
        }
    } else {
        result = " []"
    }
    return result
}

At this point we have enough to implement a program to test our tree, shown in Listing 8.4.10:

🔗

Listing 8.4.10. Sample Binary Search Tree Program

🔗

// Subinterface of MapADT that adds Comparable capability.
interface ComparableMapADT<K: Comparable<K>, V>: MapADT<K, V> {

// Return a list of all keys from fromKey to toKey, inclusive.
    fun keyList(fromKey: K, toKey: K): List<K>
}                 
interface MapADT<K, V> {
    // Adds the key/value pair to the map.
    // If the key is already in the map, it replaces the old value with the new one.
    fun put(key: K, value: V)

// Returns the value matching the provided key, or null otherwise.
    fun get(key: K): V?

// Removes the key from the map.
    // Returns the matching value stored in the map, or null otherwise.
    fun remove(key: K): V?

// Returns true if the key is in the map, false otherwise.
    fun containsKey(key: K): Boolean

// Returns the number of key/value pairs stored in the map
    fun size(): Int
}                 
class BSTMap<K : Comparable<K>, V> : ComparableMapADT<K, V>, Iterable<K> {

var root: TreeNode? = null
    var nodeCount = 0

override fun size(): Int {
        return nodeCount
    }

override fun put(key: K, value: V) {
        // Local copy for null safety
        val root = this.root
        if (root != null) {
            put(key, value, root)
        } else {
            this.root = TreeNode(key, value)
        }
        this.nodeCount += 1
    }

private fun put(key: K, value: V, currentNode: TreeNode) {
        // Local copies for null safety
        val currentLeftChild = currentNode.leftChild
        val currentRightChild = currentNode.rightChild

if (key < currentNode.key) {
            if (currentLeftChild != null) {
                put(key, value, currentLeftChild)
            } else {
                currentNode.leftChild = TreeNode(key, value, currentNode)
            }
        } else {
            if (currentRightChild != null) {
                put(key, value, currentRightChild)
            } else {
                currentNode.rightChild = TreeNode(key, value, currentNode)
            }
        }
    }

override fun get(key: K): V? {
        if (this.root != null) {
            val result = get(key, this.root)
            if (result != null) {
                return result.value
            }
        }
        return null
    }

fun get(key: K, currentNode: TreeNode?): TreeNode? {
        if (currentNode == null) {
            return null
        }
        if (key == currentNode.key) {
            return currentNode
        } else if (key < currentNode.key) {
            return get(key, currentNode.leftChild)
        } else {
            return get(key, currentNode.rightChild)
        }
    }

override fun containsKey(key: K): Boolean {
        val result = get(key, this.root)
        return (result != null)
    }

override fun remove(key: K): V? {
        val nodeToRemove = get(key, root)

if (nodeToRemove == null) {
            // Didn't find key; this handles empty tree case too
            return null
        } else if (nodeCount == 1) {
            // Node to remove must be root
            root = null
            nodeCount -= 1
            return nodeToRemove.value
        } else {
            // Node to remove must be some other node
            val valueRemoved = nodeToRemove.value
            removeNode(nodeToRemove)
            nodeCount -= 1
            return valueRemoved
        }
    }

private fun removeNode(currentNode: TreeNode) {
        // Local copies for null safety
        val currentParent = currentNode.parent
        val currentLeft = currentNode.leftChild
        val currentRight = currentNode.rightChild

if (currentNode.isLeaf()) {
            // case 1: the current node is a leaf node (no children)

// removeNode is never called if there is only a single node
            // in the tree, so this node cannot both be a leaf
            // and have no parent
            checkNotNull(currentParent)

if (currentNode == currentParent.leftChild) {
                currentParent.leftChild = null
            } else {
                currentParent.rightChild = null
            }
        } else if (currentLeft != null && currentRight == null) {
            // case 2a: one child only (left)
            adjustParent(currentNode, currentLeft)
        } else if (currentRight != null && currentLeft == null) {
            // case 2b: one child only (right)
            adjustParent(currentNode, currentRight)
        } else {
            // case 3: two children
            val successor = currentNode.findSuccessor()
            // Since two children, there must be a successor
            checkNotNull(successor)
            successor.spliceOut()
            currentNode.key = successor.key
            currentNode.value = successor.value
        }
    }

fun adjustParent(nodeToRemove: TreeNode, childOfRemoved: TreeNode) {
        // Local copies for null safety
        val nodeToRemoveParent = nodeToRemove.parent

if (nodeToRemove.isLeftChild()) {
            checkNotNull(nodeToRemoveParent)
            childOfRemoved.parent = nodeToRemove.parent
            nodeToRemoveParent.leftChild = childOfRemoved
        } else if (nodeToRemove.isRightChild()) {
            checkNotNull(nodeToRemoveParent)
            childOfRemoved.parent = nodeToRemove.parent
            nodeToRemoveParent.rightChild = childOfRemoved
        } else {
            nodeToRemove.replaceValue(
                childOfRemoved.key, childOfRemoved.value,
                childOfRemoved.leftChild, childOfRemoved.rightChild
            )
        }
    }

// Return nested list representation of tree
    override fun toString(): String {
        return stringify(this.root)
    }

fun stringify(node: TreeNode?): String {
        var result = ""
        if (node != null) {
            if (node.isLeaf()) {
                result = " [" + node.key + "]"
            } else {
                result = " [" + node.key + stringify(node.leftChild) +
                        stringify(node.rightChild) + "]"
            }
        } else {
            result = " []"
        }
        return result
    }

override fun iterator(): Iterator<K> {
        val root = this.root
        if (root == null) {
            return iterator()
        } else {
            return root.iterator()
        }
    }

override fun keyList(fromKey: K, toKey: K): List<K> {
        throw NotImplementedError("Not yet implemented")
    }

inner class TreeNode(
        var key: K,
        var value: V,
        var parent: TreeNode? = null,
        var leftChild: TreeNode? = null,
        var rightChild: TreeNode? = null
    ) : Iterable<K> {

// Is this node a left child of a parent?
        fun isLeftChild(): Boolean {
            val parent = parent  // Local copy of parent for null safety
            return parent != null && parent.leftChild == this
        }

// Is this node a right child of a parent?
        fun isRightChild(): Boolean {
            val parent = parent   // Local copy of parent for null safety
            return parent != null && parent.rightChild == this
        }

// Is this a leaf node? (Leaf nodes have no children)
        fun isLeaf(): Boolean {
            return (leftChild == null && rightChild == null)
        }

fun replaceValue(key: K, value: V, left: TreeNode?, right: TreeNode?) {
            this.key = key
            this.value = value
            this.leftChild = left
            this.rightChild = right
            this.leftChild?.parent = this
            this.rightChild?.parent = this
        }

override fun toString(): String {
            return ""
            return "key: " + key + " value: " + value + "\n  " +
                    " left: " + leftChild + " right: " + rightChild +
                    "parent: " + parent
        }

fun findSuccessor(): TreeNode? {
            var successor: TreeNode? = null

// Local copies for null safety
            val rightChild = this.rightChild
            val parent = this.parent

if (rightChild != null) {
                successor = rightChild.findMin()
            } else {
                if (parent != null) {
                    if (isLeftChild()) {
                        successor = parent
                    } else {
                        parent.rightChild = null
                        successor = parent.findSuccessor()
                        parent.rightChild = this
                    }
                }
            }
            return successor
        }

fun findMin(): TreeNode {
            var current = this
            while (current.leftChild != null) {
                current = current.leftChild!!
            }
            return current
        }

// This function self-removes a node.
        fun spliceOut() {

// Local copies for null safety
            val parent = this.parent
            val leftChild = this.leftChild
            val rightChild = this.rightChild

// spliceOut should only be legitimately be used called
            // for a node which has a parent
            checkNotNull(parent)

if (leftChild != null && rightChild != null) {
                // Two children
                throw IllegalStateException(
                    "spliceOut should never be called on a node with two children"
                )
            } else if (leftChild != null) {
                // One child, which is left
                if (this.isLeftChild()) {
                    parent.leftChild = this.leftChild
                } else {
                    parent.rightChild = this.leftChild
                }
                leftChild.parent = parent
            } else if (rightChild != null) {
                // One child, which is right
                if (this.isLeftChild()) {
                    parent.leftChild = this.rightChild
                } else {
                    parent.rightChild = this.rightChild
                }
                rightChild.parent = this.parent
            } else {
                // No children
                if (this.isLeftChild()) {
                    parent.leftChild = null
                } else {
                    parent.rightChild = null
                }
            }
        }

override fun iterator(): Iterator<K> {
            // Local copies for null safety
            val leftChild = this.leftChild
            val rightChild = this.rightChild

return iterator {
                if (leftChild != null) {
                    for (elem in leftChild) {
                        yield(elem)
                    }
                }
                yield(key)
                if (rightChild != null) {
                    for (elem in rightChild) {
                        yield(elem)
                    }
                }
            }
        }

}
}                 
^^^^
fun main() {
    val tree = BSTMap<String, String>()

tree.put("France", "Paris")
    tree.put("Japan", "Tokyo")
    tree.put("Albania", "Tirana")
    tree.put("Madagascar", "Antananarivo")
    tree.put("Zimbabwe", "Harare")
    tree.put("South Korea", "Seoul")

println(tree)

println(tree.get("Japan")) // "Tokyo"
    println(tree.get("Brazil")) // null
}

Here is its output:

🔗

[France [Albania] [Japan [] [Madagascar [] [Zimbabwe [South Korea] []]]]]
Tokyo
null

🔗

Subsection 8.4.5 Removing a Key from a Binary Search Tree

We now turn our attention to the most challenging operation on the binary search tree, the deletion of a key (see Listing 8.4.11). The first task is to find the node to delete by searching the tree. If the key is not found, there’s nothing to remove, and so we simply return null. If the key is found and there’s only one node in the tree, then this is a base case where we delete the root node. Otherwise, we call a helper function to remove the node from within the tree.

🔗

Listing 8.4.11. Method to remove an entry from the map.

🔗

override fun remove(key: K): V? {
    val nodeToRemove = get(key, root)

    if (nodeToRemove == null) {
        // Didn't find key; this handles empty tree case too
        return null
    } else if (nodeCount == 1) {
        // Node to remove must be root
        root = null
        nodeCount -= 1
        return nodeToRemove.value
    } else {
        // Node to remove must be some other node
        removeNode(nodeToRemove)
        nodeCount -= 1
        return nodeToRemove.value
    }
}

void removeNode(TreeNode currentNode) {
    // Local copies for null safety
    val currentParent = currentNode.parent
    val currentLeft = currentNode.leftChild
    val currentRight = currentNode.rightChild

    // to be determined...
}

Once we have found the node containing the key we want to delete and we know that this isn’t one of the above base cases, there are three cases that we must consider:

🔗

The node to be deleted has no children (see Figure 8.4.12).
🔗

🔗
The node to be deleted has only one child (see Figure 8.4.13).
🔗

🔗
The node to be deleted has two children (see Figure 8.4.14).
🔗

🔗

🔗

Figure 8.4.12. Deleting Node 16, a Node without Children
🔗

Figure 8.4.13. Deleting Node 25, a Node That Has a Single Child
🔗

Figure 8.4.14. Deleting Node 5, a Node with Two Children
🔗

The first case is straightforward. If the current node has no children, all that has to happen is to delete the node and remove the reference to this node in the parent. The code for this case is shown in Listing 8.4.15.

🔗

Aside: Null safety regarding parent.

Listing 8.4.15. Removing a Leaf Node

🔗

if (currentNode.isLeaf()) {
    checkNotNull(currentParent)
    if (currentNode == currentParent.leftChild) {
        currentParent.leftChild = null
    } else {
        currentParent.rightChild = null
    }
}

The second case is only slightly more complicated. If a node has only a single child, then we promote the child to take the place of its parent. The code for this case is shown in Listing 8.4.18. As you look at this code, you will see that there are six cases to consider. Since the cases are symmetric with respect to either having a left or right child, we will just discuss the case where the current node has a left child. The decision proceeds as follows:

🔗

If the current node is a left child, then we need to update the parent reference of the left child to point to the parent of the current node, and then update the left child reference of the parent to point to the current node’s left child.
🔗

🔗
If the current node is a right child, then we need to update the parent reference of the left child to point to the parent of the current node, and then update the right child reference of the parent to point to the current node’s left child.
🔗

🔗
If the current node has no parent, it must be the root. In this case we will replace the key, value, leftChild, and rightChild data by calling the replaceValue method on the root.
🔗

🔗

🔗

Figure 8.4.16 shows before-and-after diagrams of these three situations.

🔗

Figure 8.4.16. Removing a Node with One Child
🔗

In Listing 8.4.17, we have implemented a method named adjustParent to take care of the symmetric situations without having to duplicate code. It adjusts the relationships between the child of the node we want to remove and the parent of the node we want to remove.

🔗

Aside: Null safety regarding parent.

Listing 8.4.17. Adjusting Parent/Child References

🔗

fun adjustParent(nodeToRemove: TreeNode, childOfRemoved: TreeNode) {
    // Local copy for null safety
    val nodeToRemoveParent = nodeToRemove.parent

    if (nodeToRemove.isLeftChild()) {
        checkNotNull(nodeToRemoveParent)
        childOfRemoved.parent = nodeToRemove.parent
        nodeToRemoveParent.leftChild = childOfRemoved
    } else if (nodeToRemove.isRightChild()) {
        checkNotNull(nodeToRemoveParent)
        childOfRemoved.parent = nodeToRemove.parent
        nodeToRemoveParent.rightChild = childOfRemoved
    } else {
        nodeToRemove.replaceValue(
            childOfRemoved.key, childOfRemoved.value,
            childOfRemoved.leftChild, childOfRemoved.rightChild
        )
    }
}

We use this method in the portion of removeNode that handles nodes with one child. The code fragment is shown in Listing 8.4.18.

🔗

Listing 8.4.18. Removing a Node with One Child

🔗

} else if (currentLeft != null && currentRight == null) {
    // case 2a: one child only (left)
    adjustParent(currentNode, currentLeft)
} else if (currentRight != null && currentLeft == null) {
    // case 2b: one child only (right)
    adjustParent(currentNode, currentRight)

The third case is the most difficult case to handle. If a node has two children, then it is unlikely that we can simply promote one of them to take the node’s place. We can, however, search the tree for a node that can be used to replace the one scheduled for deletion. What we need is a node that will preserve the binary search tree relationships for both of the existing left and right subtrees. The node that will do this is the node that has the next-largest key in the tree. We call this node the successor, and we will look at how to find the successor shortly. The successor is guaranteed to have no more than one child, so we know how to remove it using the two cases for deletion that we have already implemented. Once the successor has been removed, we put it in the tree in place of the node to be deleted. The code to handle the third case is shown in Listing 8.4.19.

🔗

In Listing 8.4.19 we make use of the helper methods findSuccessor and spliceOut to find and remove the successor. The reason we use spliceOut is that it goes directly to the node we want to splice out and makes the right changes. We could call remove recursively, but then we would waste time searching again for the key node. The code goes after the code for removing a node with no children.

🔗

Listing 8.4.19. Removing a node with two children

🔗

} else {
    // case 3: two children
    val successor = currentNode.findSuccessor()
    // Since two children, there must be a successor
    checkNotNull(successor)
    successor.spliceOut()
    currentNode.key = successor.key
    currentNode.value = successor.value
}

The code to find the successor is shown below (see Listing 8.4.20 ) and as you can see is a method of the TreeNode class. THis code makes use of the same properties of binary search trees that cause an inorder traversal to print out the nodes in the tree from smallest to largest. There are three cases to consider when looking for the successor:

🔗

If the node has a right child, then the successor is the smallest key in the right subtree.
🔗

🔗
If the node has no right child and is the left child of its parent, then the parent is the successor.
🔗

🔗
If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.
🔗

🔗

🔗

The first condition is the only one that matters for us when deleting a node from a binary search tree. However, the findSuccessor method has other uses that we will explore in the exercises at the end of this chapter.

🔗

The findMin method is called to find the minimum key in a subtree. You should convince yourself that the minimum value key in any binary search tree is the leftmost child of the tree. Therefore the findMin method simply follows the left child references in each node of the subtree until it reaches a node that does not have a left child.

🔗

Listing 8.4.20. The findSucessor Method and Helpers

🔗

fun findSuccessor(): TreeNode? {
    var successor: TreeNode? = null

    // Local copies for null safety
    val rightChild = this.rightChild
    val parent = this.parent

    if (rightChild != null) {
        successor = rightChild.findMin()
    } else {
        if (parent != null) {
            if (isLeftChild()) {
                successor = parent
            } else {
                parent.rightChild = null
                successor = parent.findSuccessor()
                parent.rightChild = this
            }
        }
    }
    return successor
}

fun findMin(): TreeNode {
    var current = this
    while (current.leftChild != null) {
        current = current.leftChild!!
    }
    return current
}

// This function self-removes a node. It connects
fun spliceOut() {

    // Local copies for null safety
    val parent = this.parent
    val leftChild = this.leftChild
    val rightChild = this.rightChild

    // spliceOut should only be legitimately be used called
    // for a node which has a parent
    checkNotNull(parent)

    if (leftChild != null && rightChild != null) {
        // Two children
        throw IllegalStateException(
            "spliceOut should never be called on a node with two children"
        )
    } else if (leftChild != null) {
        // One child, which is left
        if (this.isLeftChild()) {
            parent.leftChild = this.leftChild
        } else {
            parent.rightChild = this.leftChild
        }
        leftChild.parent = parent
    } else if (rightChild != null) {
        // One child, which is right
        if (this.isLeftChild()) {
            parent.leftChild = this.rightChild
        } else {
            parent.rightChild = this.rightChild
        }
        rightChild.parent = this.parent
    } else {
        // No children
        if (this.isLeftChild()) {
            parent.leftChild = null
        } else {
            parent.rightChild = null
        }
    }
}

🔗

Subsection 8.4.6 Iterating over a Binary Search Tree

Suppose that we would like to iterate over all the keys in the tree in order. You already know how to traverse a binary tree in order, using the inorder traversal algorithm. However, writing an iterator is a bit different since an iterator should return only one node each time it is called.

🔗

Kotlin provides us with a very powerful function to use when creating an iterator. The function is called yield. yield is similar to return in that it returns a value to the caller. However, yield also takes the additional step of freezing the state of the function so that the next time the function is called it continues executing from the exact point it left off earlier.

🔗

We first need to notify Kotlin that a TreeNode is something we an iterate over. We do that in the header for the TreeNode class, indicating that it implements the Iterable interface:

🔗

Listing 8.4.21. Iterator for a Tree Node

🔗

inner class TreeNode(...) : Iterable<K> {
        // ...
}

We then need to write the code for an inorder iterator on a tree node, which we show in the next listing. Look at this code carefully; at first glance you might think that the code is not recursive. However, for ... in operation implicitly calls iterator, so it really is recursive! Because it is recursive over TreeNode instances, the iterator method is defined in the TreeNode class.

🔗

Listing 8.4.22. Iterator for a Tree Node

🔗

override fun iterator(): Iterator<K> {
    // Local copies for null safety
    val leftChild = this.leftChild
    val rightChild = this.rightChild

    return iterator {
        if (leftChild != null) {
            for (elem in leftChild) {
                yield(elem)
            }
        }
        yield(key)
        if (rightChild != null) {
            for (elem in rightChild) {
                yield(elem)
            }
        }
    }
}

The above works great for iterating over a tree rooted at a particular node. However, the typical user of our map will be working with the BSTMap class. We therefore need to declare that class as iterable, and include an iterator method there that will then call the iterator method on the root node.

🔗

The following shows the update we make to the header of the BSTMap class, showing that we implement the Iterable interface:

🔗

Listing 8.4.23. Updated header for BSTMap class

🔗

class BSTMap<K : Comparable<K>, V> : ComparableMapADT<K, V>, Iterable<K> {
....
}

And then here is the code for the iterator method itself.

🔗

Listing 8.4.24. Iterator method for BSTMap class

🔗

override fun iterator(): Iterator<K> {
    val root = this.root
    if (root == null) {
        return iterator()
    } else {
        return root.iterator()
    }
}

Finally, here is the complete code we have written above, with tests at the end. We have left the keyList method for you to complete as an exercise.

🔗

Listing 8.4.25. Complete Binary Search Tree Code, with Tests

🔗

// Subinterface of MapADT that adds Comparable capability.
interface ComparableMapADT<K: Comparable<K>, V>: MapADT<K, V> {

// Returns the value matching the provided key, or null otherwise.
    fun get(key: K): V?

// Removes the key from the map.
    // Returns the matching value stored in the map, or null otherwise.
    fun remove(key: K): V?

// Returns true if the key is in the map, false otherwise.
    fun containsKey(key: K): Boolean

// Returns the number of key/value pairs stored in the map
    fun size(): Int
}                 
^^^^
class BSTMap<K : Comparable<K>, V> : ComparableMapADT<K, V>, Iterable<K> {