Skip to main content
Logo image

Problem Solving with Algorithms and Data Structures using Kotlin The Interactive Edition

Bradley N. Miller, David L. Ranum, Roman Yasinovskyy, J. David Eisenberg, David R. Musicant

Section 5.10 The Merge Sort

We now turn our attention to using a divide and conquer strategy as a way to improve the performance of sorting algorithms. The first algorithm we will study is the merge sort.
🔗
Merge sort is a recursive algorithm that continually splits a list in half. If the list is empty or has one item, it is sorted by definition (the base case). If the list has more than one item, we split the list and recursively invoke a merge sort on both halves. Once the two halves are sorted, the fundamental operation, called a merge, is performed.
🔗
Merging is the process of taking two smaller sorted lists and combining them together into a single sorted new list. Figure 5.10.1 shows our familiar example list as it is being split by mergeSort. Figure 5.10.2 shows the simple lists, now sorted, as they are merged back together.
🔗
Figure 5.10.1. Splitting the List in a Merge Sort
🔗
Figure 5.10.2. Lists as They Are Merged Together
🔗
The first mergeSort function shown in Listing 5.10.3 takes an initial list, and then creates a new temporary list of the same size. It then calls a second mergeSort function which is the actual function that sets up the work; this function takes the initial list and the temporary list as parameters, as well as two integers named stop and start. These indicate the range of the list that we are currently sorting. We use the typical convention where start is inclusive and stop is exclusive, i.e. start is the first index of the range under consideration, and stop is one more than the last index.
🔗
This second mergeSort function begins by asking the base case question. If the range covered by start and stop is one or fewer items, then the sublist under consideration is already sorted and no more processing is necessary. If, on the other hand, the range size is larger than one, then we recursively call mergeSort twice, once to sort the left sublist and once to sort the right. It is important to note that the list may not have an even number of items. That does not matter, as the lengths will differ by at most one.
🔗
Listing 5.10.3. Merge Sort with Debug Output
🔗
Once the recursive calls to mergeSorton the left half and the right half (lines 19–20) are complete, it is assumed that these two halves are each sorted. The merge function is then responsible for merging the two smaller sorted half lists into a larger sorted list. Notice that the merge operation places the items into the temporary list (list) one at a time by repeatedly taking the smallest item from the sorted lists. Note that the condition in line 41 (list[left] <= list[right]) — specifically, the use of <= — ensures that the algorithm is stable. A stable algorithm maintains the order of duplicate items in a list and is preferred in most cases.
🔗
Listing 5.10.4 shows the result of executing the function on our example list. Note that the list with 44, 55, and 20 will not divide evenly. The first split gives [44] and the second gives [55, 20]. You can see how the splitting process eventually yields a list that can be immediately merged with other sorted lists.
🔗
Listing 5.10.4. Output of Merge Sort
🔗
 Start point:  [54, 26, 93, 17, 77, 31, 44, 55, 20]
 Sorting [54, 26, 93, 17, 77, 31, 44, 55, 20]
      Sorting [54, 26, 93, 17]
        Sorting [54, 26]
         Sorting [54]
         Sorting [26]
        Merged into [54, 26]
        Sorting [93, 17]
         Sorting [93]
         Sorting [17]
        Merged into [93, 17]
      Merged into [17, 54, 26, 93]
     Sorting [77, 31, 44, 55, 20]
        Sorting [77, 31]
         Sorting [77]
         Sorting [31]
        Merged into [77, 31]
       Sorting [44, 55, 20]
         Sorting [44]
        Sorting [55, 20]
         Sorting [55]
         Sorting [20]
        Merged into [55, 20]
       Merged into [20, 44, 55]
     Merged into [44, 55, 77, 31, 20]
 Merged into [17, 54, 26, 55, 77, 31, 20, 93, 44]
Final result: [17, 54, 26, 55, 77, 31, 20, 93, 44]
In order to analyze the mergeSort function, we need to consider the two distinct processes that make up its implementation. First, the list is split into halves. We already computed (in a binary search) that we can divide a list in half \(\log{n}\) times where \(n\) is the length of the list. The second process is the merge. Each item in the list will eventually be processed and placed on the sorted list. So the merge operation which results in a list of size \(n\) requires \(n\) operations. The result of this analysis is that \(\log{n}\) splits, each of which costs \(n\) for a total of \(n\log{n}\) operations. A merge sort is an \(O(n\log{n})\) algorithm.
🔗
It is important to notice that the mergeSort function requires extra space for the temporary list. This additional space can be a critical factor if the list is large and can make this sort problematic when working on large data sets.
🔗

Exercises Self Check

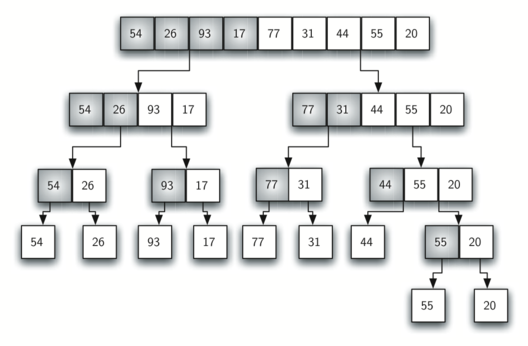
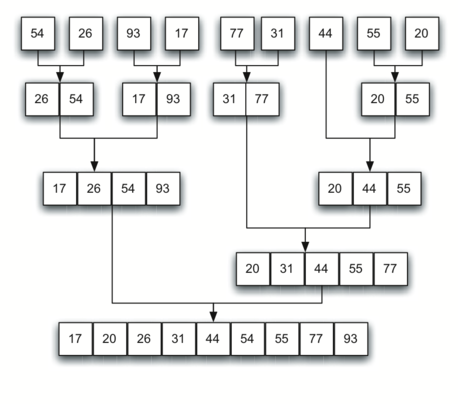
1.

Given the following list of numbers:
🔗
[21, 1, 26, 45, 29, 28, 2, 9, 16, 49, 39, 27, 43, 34, 46, 40]
🔗
which answer illustrates the list to be sorted after 3 recursive calls to mergeSort?
🔗
  • [16, 49, 39, 27, 43, 34, 46, 40]
  • This is the second half of the list.
  • [21,1]
  • Yes, mergesort will continue to recursively move toward the beginning of the list until it hits a base case.
  • [21, 1, 26, 45]
  • Remember mergesort doesn’t work on the right half of the list until the left half is completely sorted.
  • [21]
  • This is the list after 4 recursive calls
🔗

2.

Given the following list of numbers:
🔗
[21, 1, 26, 45, 29, 28, 2, 9, 16, 49, 39, 27, 43, 34, 46, 40]
🔗
which answer illustrates the first two lists to be merged?
🔗
  • [21, 1] and [26, 45]
  • The first two lists merged will be base case lists, we have not yet reached a base case.
  • [[1, 2, 9, 21, 26, 28, 29, 45] and [16, 27, 34, 39, 40, 43, 46, 49]
  • These will be the last two lists merged
  • [21] and [1]
  • The lists [21] and [1] are the first two base cases encountered by mergesort and will therefore be the first two lists merged.
  • [9] and [16]
  • Although 9 and 16 are next to each other they are in different halves of the list starting with the first split.
🔗
🔗
You have attempted of activities on this page.
🔗
PrevTopNext