DS Nodes and References

Section 7.5 Nodes and References

We will implement a binary search tree using nodes and references. Specifically, we will define a class that represents a single note in the binary tree. Because the term root often refers to the entire tree, we will refer to the value in a particular node as the key. A node therefore has attributes for the key value as well as the left and right subtrees. Using nodes and references, we might think of the tree as being structured like the one shown in Figure 7.5.1.

🔗

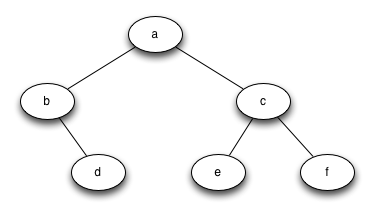
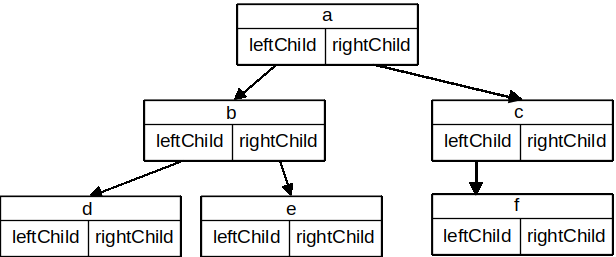
tree showing left and right children> — Figure 7.5.1. A Simple Tree Using a Nodes and References Approach
🔗

We will start out with a simple class definition for the nodes and references approach as shown in Listing 7.5.2. The important thing to remember about this representation is that the attributes leftChild and rightChild will become references to other instances of the BinaryTree class. For example, when we insert a new left child into the tree, we create another instance of BinaryTree and modify leftChild in the root to reference the new tree.

🔗

Listing 7.5.2. Binary Tree Class Setup

🔗

class BinaryTree<T>(var key: T) {
    var leftChild: BinaryTree<T>? = null
    var rightChild: BinaryTree<T>? = null

    // more code here...
}

Notice that in Listing 7.5.2, the constructor expects to get some kind of object to store as the key value for the node. We are using generics so that our trees are not restricted to holding values of only one particular type. For our early examples, we will store the name of the node as the key value. Using nodes and references to represent the tree in Figure 7.5.1, we would create six instances of the BinaryTree class.

🔗

Next let’s look at the methods we need to build the tree beyond the root node. To add a left child to the tree, we will create a new binary tree object and set the leftChild attribute of the root to refer to this new object. The code for insertLeft is shown in Listing 7.5.3.

🔗

Listing 7.5.3. insertLeft code

🔗

fun insertLeft(newNode: T): BinaryTree<T> {
     if (leftChild == null) {
         val newChild = BinaryTree(newNode)
         leftChild = newChild
         return newChild
     } else {
         val newChild = BinaryTree(newNode)
         newChild.leftChild = leftChild
         leftChild = newChild
         return newChild
     }
 }

We must consider two cases for insertion. The first case is characterized by a node with no existing left child. When there is no left child, we add a node to the tree. The second case is characterized by a node with an existing left child. In the second case, we insert a node and push the existing child down one level in the tree. The second case is handled by the else statement on line 6 of Listing 7.5.3. In both cases, we then return the new node that has been created. For the test code in this section, we just ignore this return value, but it is helpful in future sections to be able to have easy access to the subtree that was just created and to know that it is not null.

🔗

The code for insertRight must consider a symmetric set of cases. There will either be no right child, or we must insert the node between the root and an existing right child. The insertion code is shown in Listing 7.5.4.

🔗

Listing 7.5.4. insertRight code

🔗

fun insertRight(newNode: T): BinaryTree<T> {
    if (rightChild == null) {
        val newChild = BinaryTree(newNode)
        rightChild = newChild
        return newChild
    } else {
        val newChild = BinaryTree(newNode)
        newChild.rightChild = rightChild
        rightChild = newChild
        return newChild
    }
}

Now that we have all the pieces to create and manipulate a binary tree, let’s use them to check on the structure a bit more. Let’s make a simple tree with node a as the root, and add nodes “b” and “c” as children. Listing 7.5.5 creates the tree and looks at the some of the values stored in key, leftChild, and rightChild. Notice that both the left and right children of the root are themselves distinct instances of the BinaryTree class. As we said in our original recursive definition for a tree, this allows us to treat any child of a binary tree as a binary tree itself.

🔗

In this test code, we often use the !! operator to ignore null safety checks. We are choosing in this example to do so to keep the code brief, to make it easier to see what’s happening.

🔗

Listing 7.5.5. Test Program for BinaryTree Class

🔗

class BinaryTree<T>(var key: T) {
    var leftChild: BinaryTree<T>? = null
    var rightChild: BinaryTree<T>? = null

fun insertLeft(newNode: T): BinaryTree<T> {
        if (leftChild == null) {
            val newChild = BinaryTree(newNode)
            leftChild = newChild
            return newChild
        } else {
            val newChild = BinaryTree(newNode)
            newChild.leftChild = leftChild
            leftChild = newChild
            return newChild
        }
    }

fun insertRight(newNode: T): BinaryTree<T> {
        if (rightChild == null) {
            val newChild = BinaryTree(newNode)
            rightChild = newChild
            return newChild
        } else {
            val newChild = BinaryTree(newNode)
            newChild.rightChild = rightChild
            rightChild = newChild
            return newChild
        }
    }

fun preorder() {
        println(this.key)
        leftChild?.preorder()
        rightChild?.preorder()
    }

}
^^^^
fun main() {
    val aTree = BinaryTree("a")

println(aTree.key) // "a"
    println(aTree.leftChild) // null

aTree.insertLeft("b")
    println(aTree.leftChild) // reference to BinaryTree
    println(aTree.leftChild!!.key) // "b"

aTree.insertRight("c")
    println(aTree.rightChild) // reference to BinaryTree
    println(aTree.rightChild!!.key) // "c"

aTree.rightChild!!.key = "d"
    println(aTree.rightChild!!.key) // "d"
}

Exercises Self Check

1.

Write a function named buildTree that returns a tree using the nodes and references implementation that looks like this:

🔗

You have attempted of activities on this page.

🔗

Prev Top Next