Problem Solving with Algorithms and Data Structures using Kotlin The Interactive Edition

A more space-efficient way to implement a sparsely connected graph is to use what has historically been called an adjacency list. In the classic version of the adjacency list implementation, we keep a master list of all the vertices in our Graph object, and each vertex object in the graph maintains a list of the other vertices that it is connected to. Figure 10.5.1 illustrates an adjacency list representation for the graph in Section 10.2.

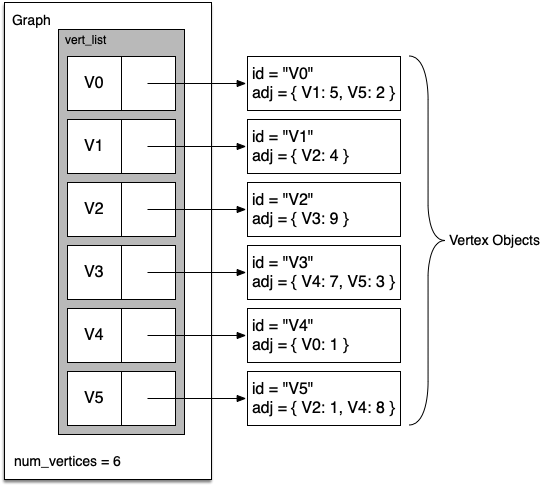
The advantage of the adjacency list implementation is that it allows us to compactly represent a sparse graph. The adjacency list also allows us to easily find all the links that are directly connected to a particular vertex.

Most modern implementations of the "adjacency list" approach, ironically, don’t actually use lists. This is because lists are inefficient for this purpose. To find a particular vertex, we would need to do sequential search through the list to find it (unless our vertices are identified via consecutive integer values starting from 0, which are generally only found in textbook examples). Therefore, instead of using a list to represent the vertices, we will use a map. The keys in the map will be the vertex IDs, where the ID for a vertex is a unique value of some kind that identifies that vertex. The map will then store a connection between each vertex id and a collection of neighbors. To visualize this, look at Figure 10.5.1, but use a map to store the gray boxes on the left labeled as vert_list.

More precisely, what do we mean by the "collection of neighbors" for each vertex? If the graph is an unweighted graph, the collection of neighbors for each vertex can be represented as a set of adjacent vertex IDs. If the graph is a weighted graph, the collection of neighbors can be a map containing adjacent vertex IDs, and the weight of the connection for each. To visualize this, look again at Figure 10.5.1, but use a map for the six lists labeled as adj.

For our implementation, we will use this "map of maps" approach. We will continue to follow historical precedent and refer to this as an "adjacency list" approach, though we acknowledge that "adjacency map" would be a better name.