Skip to main content
Logo image

Applied Discrete Structures

Al Doerr, Ken Levasseur

Appendix D Hints and Solutions to Selected Exercises

For the most part, solutions are provided here for odd-numbered exercises.

1 Set Theory
1.1 Set Notation and Relations
1.1.3 Exercises for Section 1.1

1.1.3.1.

Answer.
These answers are not unique.
  1. \(\displaystyle 8, 15, 22, 29\)
  2. \(\displaystyle \textrm{apple, pear, peach, plum}\)
  3. \(\displaystyle 1/2, 1/3, 1/4, 1/5\)
  4. \(\displaystyle -8, -6, -4, -2\)
  5. \(\displaystyle 6, 10, 15, 21\)

1.1.3.3.

Answer.
  1. \(\displaystyle \{2k + 1 \mid k \in \mathbb{Z}, 2 \leqslant k \leqslant 39\}\)
  2. \(\displaystyle \{x \in \mathbb{Q}\mid -1 < x < 1\}\)
  3. \(\displaystyle \{2n\mid n \in \mathbb{Z}\}\)
  4. \(\displaystyle \{9n\mid n \in \mathbb{Z}, -2 \leq n\}\)

1.1.3.5.

Answer.
  1. True
  2. False
  3. True
  4. True
  5. False
  6. True
  7. False
  8. True

1.1.3.7.

Answer.
\(\{\emptyset\}\) is not the empty set - it contains something which happens to be the empty set.

1.2 Basic Set Operations
1.2.4 Exercises

1.2.4.1.

Answer.
  1. \(\displaystyle \{2,3\}\)
  2. \(\displaystyle \{0,2,3\}\)
  3. \(\displaystyle \{0,2,3\}\)
  4. \(\displaystyle \{0,1,2,3,5,9\}\)
  5. \(\displaystyle \{0\}\)
  6. \(\displaystyle \emptyset\)
  7. \(\displaystyle \{ 1,4,5,6,7,8,9\}\)
  8. \(\displaystyle \{0,2,3,4,6,7,8\}\)
  9. \(\displaystyle \emptyset\)
  10. \(\displaystyle \{0\}\)

1.2.4.3.

Answer.
These are all true for any sets \(A\text{,}\) \(B\text{,}\) and \(C\text{.}\)

1.2.4.5.

Answer.
  1. \(\displaystyle \{1, 4\} \subseteq A \subseteq \{1, 2, 3, 4\}\)
  2. \(\displaystyle \{2\} \subseteq A \subseteq \{1, 2, 4, 5\}\)
  3. \(\displaystyle A = \{2, 4, 5\}\)

1.2.4.7.

Answer.
Solution to #7 of section 1.2
Figure 1.2.18.

1.3 Cartesian Products and Power Sets
1.3.4 Exercises

1.3.4.1.

Answer.
  1. \(\displaystyle \{(0, 2), (0, 3), (2, 2), (2, 3), (3, 2), (3, 3)\}\)
  2. \(\displaystyle \{(2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (3, 3)\}\)
  3. \(\displaystyle \{(0, 2, 1), (0, 2, 4), (0, 3, 1), (0, 3, 4), (2, 2, 1), (2, 2, 4),\\ (2, 3, 1), (2, 3, 4), (3, 2, 1), (3, 2, 4), (3, 3, 1), (3, 3, 4)\}\)
  4. \(\displaystyle \emptyset\)
  5. \(\displaystyle \{(0, 1), (0, 4), (2, 1), (2, 4), (3, 1), (3, 4)\}\)
  6. \(\displaystyle \{(2, 2), (2, 3), (3, 2), (3, 3)\}\)
  7. \(\displaystyle \{(2, 2, 2), (2, 2, 3), (2, 3, 2), (2, 3, 3), (3, 2, 2), (3, 2, 3), (3, 3, 2), (3, 3, 3)\}\)
  8. \(\displaystyle \{(2, \emptyset ), (2, \{2\}), (2, \{3\}), (2, \{2, 3\}), (3, \emptyset ), (3, \{2\}), (3, \{3\}), (3, \{2, 3\})\}\)

1.3.4.3.

Answer.
\(\{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\} \textrm{ and } \{c, d\}\)

1.3.4.5.

Answer.
There are \(n\) singleton subsets, one for each element.

1.3.4.7.

Answer.
  1. \(\displaystyle \{+00, +01, +10, +11, -00, -01, -10, -11\}\)
  2. \(\displaystyle 16 \textrm{ and } 512\)

1.3.4.9.

Answer.
They are equal when \(A=B\text{.}\)

1.4 Binary Representation of Positive Integers
1.4.3 Exercises

1.4.3.1.

Answer.
  1. \(\displaystyle 11111\)
  2. \(\displaystyle 100000\)
  3. \(\displaystyle 1010\)
  4. \(\displaystyle 1100100\)

1.4.3.3.

Answer.
  1. \(\displaystyle 18\)
  2. \(\displaystyle 19\)
  3. \(\displaystyle 42\)
  4. \(\displaystyle 1264\)

1.4.3.5.

Answer.
There is a bit for each power of 2 up to the largest one needed to represent an integer, and you start counting with the zeroth power. For example, 2017 is between \(2^{10}=1024\) and \(2^{11}=2048\text{,}\) and so the largest power needed is \(2^{10}\text{.}\) Therefore there are \(11\) bits in binary 2017.
  1. \(\displaystyle 11\)
  2. \(\displaystyle 12\)
  3. \(\displaystyle 13\)
  4. 51

1.4.3.7.

Answer.
A number must be a multiple of four if its binary representation ends in two zeros. If it ends in \(k\) zeros, it must be a multiple of \(2^k\text{.}\)

1.5 Summation Notation and Generalizations
1.5.3 Exercises

1.5.3.1.

Answer.
  1. \(\displaystyle 24\)
  2. \(\displaystyle 6\)
  3. \(\displaystyle 3,7,15,31\)
  4. \(\displaystyle 1,4,9,16\)

1.5.3.3.

Answer.
  1. \(\displaystyle \frac{1}{1 (1+1)}+\frac{1}{2 (2+1)}+\frac{1}{3 (3+1)}+\cdots +\frac{1}{n(n+1)}=\frac{n}{n+1}\)
  2. \(\displaystyle \frac{1}{1(2)}+\frac{1}{2(3)}+\frac{1}{3(4)}=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}=\frac{3}{4}=\frac{3}{3+1}\)
  3. \(1+2^3+3^3+\cdots +n^3=\left(\frac{1}{4}\right)n^2(n+1)^2\) \(\quad 1+8+27=36 = \left(\frac{1}{4}\right)(3)^2(3+1)^2\)

1.5.3.5.

Answer.
\((x+y)^3=\left(\text{}_0^3\right)x^3+\left(\text{}_1^3\right)x^{2}y+\left.(_2^3\right)x y^2+\left(\text{}_3^3\right)y^3\)

1.5.3.7.

Answer.
  1. \(\displaystyle \{x\in \mathbb{Q}\mid 0 < x \leq 5\}\)
  2. \(\displaystyle \{x\in \mathbb{Q}\mid -5 < x < 5\}=B_5\)
  3. \(\displaystyle \emptyset\)
  4. \(\displaystyle \{x\in \mathbb{Q}\mid -1 < x < 1\}=B_1\)

1.5.3.9.

Answer.
  1. \(\displaystyle 36\)
  2. \(\displaystyle 105\)

2 Combinatorics
2.1 Basic Counting Techniques - The Rule of Products
2.1.3 Exercises

2.1.3.1.

Answer.
If there are \(m\) horses in race 1 and \(n\) horses in race 2 then there are \(m \cdot n\) possible daily doubles.

2.1.3.3.

Answer.
\(72=4\cdot 6\cdot 3\)

2.1.3.5.

Answer.
\(720=6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1\)

2.1.3.7.

Answer.
If we always include the blazer in the outfit we would have 6 outfits. If we consider the blazer optional then there would be 12 outfits. When we add a sweater we have the same type of choice. Considering the sweater optional produces 24 outfits.

2.1.3.9.

Answer.
  1. \(\displaystyle 2^8=256\)
  2. \(2^4=16\text{.}\) Here we are concerned only with the first four bits, since the last four are a mirror image of the first four.
  3. \(2^7=128\text{,}\) you have no choice in the last bit.

2.1.3.11.

Answer.
  1. \(\displaystyle 16\)
  2. \(\displaystyle 31\)
In the second part we can arrive at the answer by counting all subsets and subtracting one since one of the sets (the whole set) is an improper subsets.

2.1.3.13.

Answer.
  1. \(\displaystyle 3\)
  2. \(\displaystyle 6\)

2.1.3.15.

Answer.
\(18\)

2.1.3.17.

Answer.
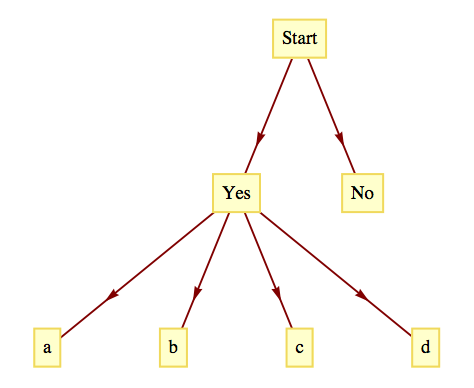
solution to exercise 17a of section 2.1. From a start node, there are two branches. The first branch, labeled yes, has four branches coming from it, one for each of the possible follow-up responses. The second branch from start is an end branch labeled no.
Figure 2.1.10. Solution to 17(a)
  1. See Figure 2.1.10
  2. \(\displaystyle 5^6\)

2.1.3.19.

Answer.
\(2^{n-1}-1\) and \(2^n-2\)

2.2 Permutations
2.2.2 Exercises

2.2.2.1.

Answer.
\(P(1000,3)\)

2.2.2.3.

Answer.
With repetition: \(26^8\approx 2.0883\times 10^{11}\)
Without repetition: \(P(26,8) \approx 6.2991\ 10^{10}\)

2.2.2.5.

Answer.
\(15!\)

2.2.2.7.

Answer.
  1. \(\displaystyle P(15,5)=360360\)
  2. \(\displaystyle 2\cdot 14\cdot 13\cdot 12\cdot 11=48048\)

2.2.2.9.

Answer.
If the president is sitting at 12 o’clock on the table, then the two members from her major need to sit at 4 and 8 o’clock. There are two ways to arrange them. The other majors sit at 2, 6, and 10 o’clock and can be placed \(P(3,3)=6\) ways, so the final answer is \(2 \times 6 = 12\)

2.2.2.11.

Answer.
  1. \(\displaystyle P(4,2)=12\)
  2. \(\displaystyle P(n;2)=n(n-1)\)
  3. Case 1: \(m>n\text{.}\) Since the coordinates must be different, this case is impossible.
    Case 2: \(m\leqslant n. P(n;m)\text{.}\)

2.3 Partitions of Sets and the Law of Addition
2.3.3 Exercises

2.3.3.1.

Answer.
\(\{\{a\}, \{b\}, \{c\}\}, \{\{a, b\}, \{c\}\}, \{\{a, c\}, \{b\}\}, \{\{a\}, \{b, c\}\}, \{\{a, b, c\}\}\)

2.3.3.3.

Answer.
No. By this definition it is possible that an element of \(A\) might belong to two of the subsets.

2.3.3.5.

Answer.
The first subset is all the even integers and the second is all the odd integers. These two sets do not intersect and they cover the integers completely.

2.3.3.7.

Answer.
Since 17 participated in both activities, 30 of the tennis players only played tennis and 25 of the swimmers only swam. Therefore, \(17+30+25=72\) of those who were surveyed participated in an activity and so 18 did not.

2.3.3.9.

Solution.
We assume that \(\lvert A_1 \cup A_2 \rvert = \lvert A_1 \rvert +\lvert A_2\rvert -\lvert A_1\cap A_2\rvert \text{.}\)
\begin{equation*} \begin{split} \lvert A_1 \cup A_2\cup A_3 \rvert & =\lvert (A_1\cup A_2) \cup A_3 \rvert \quad Why?\\ & = \lvert A_1\cup A_2\rvert +\lvert A_3 \rvert -\lvert (A_1\cup A_2)\cap A_3\rvert \quad Why? \\ & =\lvert (A_1\cup A_2\rvert +\lvert A_3\rvert -\lvert (A_1\cap A_3)\cup (A_2\cap A_3)\rvert \quad Why?\\ & =\lvert A_1\rvert +\lvert A_2\rvert -\lvert A_1\cap A_2\rvert +\lvert A_3\rvert \\ & \quad -(\lvert A_1\cap A_3\rvert +\lvert A_2\cap A_3\rvert -\lvert (A_1\cap A_3)\cap (A_2\cap A_3)\rvert\quad Why?\\ & =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert\\ & \quad -\lvert A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_3\rvert \quad Why? \end{split} \end{equation*}
The law for four sets is
\begin{equation*} \begin{split} \lvert A_1\cup A_2\cup A_3\cup A_4\rvert & =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert +\lvert A_4\rvert\\ & \quad -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert -\lvert A_1\cap A_4\rvert \\ & \quad \quad -\lvert A_2\cap A_3\rvert -\lvert A_2\cap A_4\rvert -\lvert A_3\cap A_4\rvert \\ & \quad +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_4\rvert \\ & \quad \quad +\lvert A_1\cap A_3\cap A_4\rvert +\lvert A_2\cap A_3\cap A_4\rvert \\ & \quad -\lvert A_1\cap A_2\cap A_3\cap A_4\rvert \end{split} \end{equation*}
Derivation:
\begin{equation*} \begin{split} \lvert A_1\cup A_2\cup A_3\cup A_4\rvert & = \lvert (A_1\cup A_2\cup A_3)\cup A_4\rvert \\ & = \lvert (A_1\cup A_2\cup A_3\rvert +\lvert A_4\rvert -\lvert (A_1\cup A_2\cup A_3)\cap A_4\rvert\\ & = \lvert (A_1\cup A_2\cup A_3\rvert +\lvert A_4\rvert \\ & \quad -\lvert (A_1\cap A_4)\cup (A_2\cap A_4)\cup (A_3\cap A_4)\rvert \\ & = \lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert \\ & \quad -\lvert A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_4\rvert -\lvert A_1\cap A_4\rvert \\ & \quad+\lvert A_2\cap A_4\rvert +\lvert A_3\cap A_4\rvert -\lvert (A_1\cap A_4)\cap (A_2\cap A_4)\rvert \\ & \quad -\lvert (A_1\cap A_4)\cap (A_3\cap A_4)\rvert -\lvert (A_2\cap A_4)\cap (A_3\cap A_4)\rvert \\ & \quad +\lvert (A_1\cap A_4)\cap (A_2\cap A_4)\cap (A_3\cap A_4)\rvert \\ & =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert +\lvert A_4\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert \\ & \quad -\lvert A_2\cap A_3\rvert -\lvert A_1\cap A_4\rvert -\lvert A_2\cap A_4\rvert \quad -\lvert A_3\cap A_4\rvert \\ & \quad +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_4\rvert \\ & \quad +\lvert A_1\cap A_3\cap A_4\rvert +\lvert A_2\cap A_3\cap A_4\rvert \\ & \quad -\lvert A_1\cap A_2 \cap A_3\cap A_4\rvert \end{split} \end{equation*}

2.3.3.11.

Answer.
Partition the set of fractions into blocks, where each block contains fractions that are numerically equivalent. Describe how you would determine whether two fractions belong to the same block. Redefine the rational numbers to be this partition. Each rational number is a set of fractions.

2.4 Combinations and the Binomial Theorem
2.4.4 Exercises

2.4.4.1.

Answer.
\(\binom{10}{3}\cdot \binom{25}{4}=1,518,000\)

2.4.4.2.

Hint.
Think of the set of positions that contain a 1 to turn this is into a question about sets.

2.4.4.3.

Answer.
\(\binom{10}{7} +\binom{10}{8} +\binom{10}{9} +\binom{10}{10}= 120+45+10+1=176 \)

2.4.4.5.

Hint.
Think of each path as a sequence of instructions to go right (R) and up (U).
Answer.
Each path can be described as a sequence or R’s and U’s with exactly six of each. The six positions in which R’s could be placed can be selected from the twelve positions in the sequence \(\binom{12}{6} =924\) ways. We can generalize this logic and see that there are \(\binom{m+n}{m}\) paths from \((0,0)\) to \((m,n)\text{.}\)

2.4.4.7.

Answer.
  1. \(\displaystyle C(52,5)=2,598,960\)
  2. \(\displaystyle \binom{52}{5}\cdot \binom{47}{5}\cdot \binom{42}{5}\cdot \binom{37}{5}\)

2.4.4.9.

Answer.
\(\binom{4}{2} \cdot \binom{48}{3} = 6 \cdot 17296=103776\)

2.4.4.11.

Answer.
\(\binom{12}{3}\cdot\binom{9}{4}\cdot\binom{5}{5}\)

2.4.4.13.

Answer.
  1. \(\displaystyle \binom{10}{2}=45\)
  2. \(\displaystyle \binom{10}{3}=120\)

2.4.4.15.

Answer.
Assume \(\lvert A \rvert =n\text{.}\) If we let \(x=y=1\) in the Binomial Theorem, we obtain \(2^n=\binom{n}{0}+\binom{n}{1}+\cdots +\binom{n}{n}\text{,}\) with the right side of the equality counting all subsets of \(A\) containing \(0, 1, 2, \dots , n\) elements. Hence \(\lvert P(A)\rvert =2^{\lvert A \rvert}\)

2.4.4.17.

Hint.
\(9998 = 10000-2\)
Answer.
\(10000^3 - 3 \cdot 2 \cdot 10000^2 +3 \cdot 2^2 \cdot 10000 - 2^3 = 999,400,119,992.\)

3 Logic
3.1 Propositions and Logical Operators
3.1.3 Exercises

3.1.3.1.

Answer.
  1. \(\displaystyle d\land c\)
  2. \(\displaystyle s\lor \neg c\)
  3. \(\displaystyle \neg (d\land s)\)
  4. \(\displaystyle \neg s\land \neg c\)

3.1.3.3.

Answer.
  1. \(2>5\) and 8 is an even integer. False.
  2. If \(2\leqslant 5\) then 8 is an even integer. True.
  3. If \(2\leqslant 5\) and 8 is an even integer then 11 is a prime number. True.
  4. If \(2\leqslant 5\) then either 8 is an even integer or 11 is not a prime number. True.
  5. If \(2\leqslant 5\) then either 8 is an odd integer or 11 is not a prime number. False.
  6. If 8 is not an even integer then \(2>5\text{.}\) True.

3.1.3.5.

Answer.
Only the converse of \(d\) is true. The converse of (a) is “It it necessary for an integer to be a even that it be a multiple of four.” This is false because 6 is even and it isn’t a multiple of four.

3.2 Truth Tables and Propositions Generated by a Set
3.2.3 Exercises

3.2.3.1.

Answer.
  1. \(\displaystyle \begin{array}{cc} p & p\lor p \\ \hline 0 & 0 \\ 1 & 1 \\ \end{array}\)
  2. \(\displaystyle \begin{array}{ccc} p & \neg p & p\land (\neg p) \\ \hline 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{array}\)
  3. \(\displaystyle \begin{array}{ccc} p & \neg p & p\lor (\neg p) \\ \hline 0 & 1 & 1 \\ 1 & 0 & 1 \\ \end{array}\)
  4. \(\displaystyle \begin{array}{cc} p & p\land p \\ \hline 0 & 0 \\ 1 & 1 \\ \end{array}\)

3.2.3.3.

Answer.
  1. \(\displaystyle \neg (p\land r) \lor s\)
  2. \(\displaystyle (p\lor q) \land (r\lor q)\)

3.2.3.5.

Answer.
\(2^4 = 16\) rows.

3.3 Equivalence and Implication
3.3.5 Exercises

3.3.5.1.

Answer.
\(a\Leftrightarrow e, d\Leftrightarrow f, g\Leftrightarrow h\)

3.3.5.3.

Solution.
No. In symbolic form the question is: Is \((p\to q)\Leftrightarrow (q\to p)\text{?}\) \(\begin{array}{ccccc} p & q & p\to q & q\to p & (p\to q)\leftrightarrow (q\to p) \\ \hline 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 0\\ 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ \end{array}\)
This table indicates that an implication is not always equivalent to its converse.

3.3.5.5.

Solution.
Let \(x\) be any proposition generated by \(p\) and \(q\text{.}\) The truth table for \(x\) has 4 rows and there are 2 choices for a truth value for \(x\) for each row, so there are \(2\cdot 2\cdot 2\cdot 2=2^4\) possible propositions.

3.3.5.7.

Answer.
\(0\to p\) and \(p\to 1\) are tautologies.

3.3.5.9.

Solution.
Yes. In symbolic form the question is whether, if we have a conditional proposition \(p \to q\text{,}\) is \((q\to p)\Leftrightarrow (\neg p\to \neg q)\text{?}\)
\(\begin{array}{ccccc} p & q & q\to p & \neg p\to \neg q & (q \to p)\leftrightarrow (\neg p\to \neg q) \\ \hline 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 0 & 0 & 1\\ 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ \end{array}\)
This table indicates that an converse is always equivalent to the inverse.

3.4 The Laws of Logic
3.4.2 Exercises

3.4.2.1.

Answer.
Let \(s=\textrm{I will study}\text{,}\)\(t=\textrm{I will learn.}\) The argument is: \(((s\to t)\land (\neg t))\to (\neg s) ,\) call the argument \(a\text{.}\)
\begin{equation*} \begin{array}{ccccc} s\text{ } & t\text{ } & s\to t\text{ } & (s\to t)\land (\neg t)\text{ } & a \\ \hline 0\text{ } & 0\text{ } & 1\text{ } & 1\text{ } & 1 \\ 0\text{ } & 1\text{ } & 1\text{ } & 0\text{ } & 1 \\ 1\text{ } & 0\text{ } & 0\text{ } & 0\text{ } & 1 \\ 1\text{ } & 1\text{ } & 1\text{ } & 0\text{ } & 1 \\ \end{array}\text{.} \end{equation*}
Since \(a\) is a tautology, the argument is valid.

3.4.2.3.

Answer.
In any true statement \(S\text{,}\) replace; \(\land\) with \(\lor\text{,}\) \(\lor\) with \(\land\text{,}\) 0 with 1, 1 with 0, \(\Leftarrow\) with \(\Rightarrow \text{,}\) and \(\Rightarrow \) with \(\Leftarrow \text{.}\) Leave all other connectives unchanged.

3.5 Mathematical Systems and Proofs
3.5.4 Exercises

3.5.4.1.

Answer.
  1. \begin{equation*} \begin{array}{cccc} p & q & (p\lor q)\land \neg q & ((p\lor q)\land \neg q)\to p \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ \end{array} \end{equation*}
  2. \begin{equation*} \begin{array}{ccccc} p & q & (p\to q)\land \neg q & \neg p & (p\to q)\land (\neg q) \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 \\ \end{array} \end{equation*}

3.5.4.3.

Answer.
  1. Direct proof:
    1. \(\displaystyle d\to (a\lor c)\)
    2. \(\displaystyle d\)
    3. \(\displaystyle a\lor c\)
    4. \(\displaystyle a\to b\)
    5. \(\displaystyle \neg a \lor b\)
    6. \(\displaystyle c\to b\)
    7. \(\displaystyle \neg c\lor b\)
    8. \(\displaystyle (\neg a\lor b)\land (\neg c\lor b)\)
    9. \(\displaystyle (\neg a\land \neg c) \lor b\)
    10. \(\displaystyle \neg (a\lor c)\lor b\)
    11. \(b\) \(\blacksquare\)
    Indirect proof:
    1. \(\neg b\quad \) Negated conclusion
    2. \(a\to b\quad \) Premise
    3. \(\neg a\quad \) Indirect Reasoning (1), (2)
    4. \(c\to b\quad \) Premise
    5. \(\neg c\quad \) Indirect Reasoning (1), (4)
    6. \((\neg a\land \neg c)\quad \) Conjunctive (3), (5)
    7. \(\neg (a\lor c)\quad \) DeMorgan’s law (6)
    8. \(d\to (a\lor c)\quad \) Premise
    9. \(\neg d\quad \) Indirect Reasoning (7), (8)
    10. \(d\quad \) Premise
    11. \(\mathbb{0} \quad \) (9), (10) \(\quad \blacksquare\)
  2. Direct proof:
    1. \(\displaystyle (p\to q)\land (r\to s)\)
    2. \(\displaystyle p\to q\)
    3. \(\displaystyle (p\to t)\land (s\to u)\)
    4. \(\displaystyle q\to t\)
    5. \(\displaystyle p\to t\)
    6. \(\displaystyle r\to s\)
    7. \(\displaystyle s\to u\)
    8. \(\displaystyle r\to u\)
    9. \(\displaystyle p\to r\)
    10. \(\displaystyle p\to u\)
    11. \(p\to (t\land u)\) Use \((x\to y)\land (x\to z)\Leftrightarrow x\to (y\land z)\)
    12. \(\displaystyle \neg (t\land u)\to \neg p\)
    13. \(\displaystyle \neg (t\land u)\)
    14. \(\neg p\) \(\quad \blacksquare\)
    Indirect proof:
    1. \(\displaystyle p\)
    2. \(\displaystyle p\to q\)
    3. \(\displaystyle q\)
    4. \(\displaystyle q\to t\)
    5. \(\displaystyle t\)
    6. \(\displaystyle \neg (t\land u)\)
    7. \(\displaystyle \neg t\lor \neg u\)
    8. \(\displaystyle \neg u\)
    9. \(\displaystyle s\to u\)
    10. \(\displaystyle \neg s\)
    11. \(\displaystyle r\to s\)
    12. \(\displaystyle \neg r\)
    13. \(\displaystyle p\to r\)
    14. \(\displaystyle r\)
    15. \(0\) \(\quad \blacksquare\)
  3. Direct proof:
    1. \(\neg s\lor p\quad \) Premise
    2. \(s\quad \) Added premise (conditional conclusion)
    3. \(\neg (\neg s)\quad \) Involution (2)
    4. \(p \quad \) Disjunctive simplification (1), (3)
    5. \(p\to (q\to r)\quad \) Premise
    6. \(q\to r\quad \) Detachment (4), (5)
    7. \(q \quad\) Premise
    8. \(r\quad \) Detachment (6), (7) \(\blacksquare\)
    Indirect proof:
    1. \(\neg (s\to r)\quad \) Negated conclusion
    2. \(\neg (\neg s\lor r)\quad \) Conditional equivalence (1)
    3. \(s\land \neg r\quad \) DeMorgan (2)
    4. \(s\quad\) Conjunctive simplification (3)
    5. \(\neg s\lor p\quad \) Premise
    6. \(s\to p\quad\) Conditional equivalence (5)
    7. \(p \quad\) Detachment (4), (6)
    8. \(p\to (q\to r)\quad\) Premise
    9. \(q\to r \quad\) Detachment (7), (8)
    10. \(q\quad \) Premise
    11. \(r\quad\) Detachment (9), (10)
    12. \(\neg r \quad\) Conjunctive simplification (3)
    13. \(0 \quad\) Conjunction (11), (12) \(\blacksquare\)
  4. Direct proof:
    1. \(\displaystyle p\to q\)
    2. \(\displaystyle q\to r\)
    3. \(\displaystyle p\to r\)
    4. \(\displaystyle p\lor r\)
    5. \(\displaystyle \neg p\lor r\)
    6. \(\displaystyle (p\lor r)\land (\neg p\lor r)\)
    7. \(\displaystyle (p\land \neg p)\lor r\)
    8. \(\displaystyle 0\lor r\)
    9. \(r\)\(\blacksquare\)
    Indirect proof:
    1. \(\neg r\) Negated conclusion
    2. \(p\lor r\quad\) Premise
    3. \(p\quad\) (1), (2)
    4. \(p\to q\quad\) Premise
    5. \(q \quad \) Detachment (3), (4)
    6. \(q\to r\quad\) Premise
    7. \(r \quad \)Detachment (5), (6)
    8. \(0 \quad\) (1), (7) \(\blacksquare\)

3.5.4.5.

Answer.
  1. Let \(W\) stand for “Wages will increase,” \(I\) stand for “there will be inflation,” and \(C\) stand for “cost of living will increase.” Therefore the argument is: \(W\to I,\text{ }\neg I\to \neg C,\text{ }W\Rightarrow C\text{.}\) The argument is invalid. The easiest way to see this is through a truth table, which has one case, the seventh, that this false. Let \(x\) be the conjunction of all premises. \(\begin{array}{ccccccccc} W & I & C & \neg I & \neg C & W\to I & \neg I\to \neg C & x & x\to C \\ \hline 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 \\ \end{array}\)
  2. Let \(r\) stand for “the races are fixed,” \(c\) stand for “casinos are crooked,” \(t\) stand for “the tourist trade will decline,” and \(p\) stand for “the police will be happy.” Therefore, the argument is:
    \begin{equation*} (r\lor c)\to t, t\to p, \neg p\to \neg r\text{.} \end{equation*}
    The argument is valid. Proof:
    1. \(t\to p\quad \) Premise
    2. \(\neg p\quad \) Premise
    3. \(\neg t\quad \) Indirect Reasoning (1), (2)
    4. \((r\lor c)\to t\quad \) Premise
    5. \(\neg (r\lor c)\quad \) Indirect Reasoning (3), (4)
    6. \((\neg r)\land (\neg c)\quad \) DeMorgan (5)
    7. \(\neg r\quad \) Conjunction simplification \((6)\text{ }\blacksquare\)

3.5.4.7.

Answer.
\(p_1\to p_k\) and \(p_k\to p_{k+1}\) implies \(p_1\to p_{k+1}\text{.}\) It takes two steps to get to \(p_1\to p_{k+1}\) from \(p_1\to p_k\) This means it takes \(2(100-1)\) steps to get to \(p_1\to p_{100}\) (subtract 1 because \(p_1\to p_2\) is stated as a premise). A final step is needed to apply detachment to imply \(p_{100}\)

3.6 Propositions over a Universe
3.6.3 Exercises

3.6.3.1.

Answer.
  1. \(\displaystyle \{\{1\},\{3\},\{1,3\},\emptyset\}\)
  2. \(\displaystyle \{\{3\}, \{3,4\}, \{3,2\}, \{2,3,4\}\}\)
  3. \(\displaystyle \{\{1\}, \{1,2\}, \{1,3\}, \{1,4\}, \{1,2,3\}, \{1,2,4\}, \{1,3,4\}, \{1,2,3,4\}\}\)
  4. \(\displaystyle \{\{2\}, \{3\}, \{4\}, \{2,3\}, \{2,4\}, \{3,4\}\}\)
  5. \(\displaystyle \{A\subseteq U:\left| A\right| =2\}\)

3.6.3.3.

Answer.
There are \(2^3=8\) subsets of \(U\text{,}\) allowing for the possibility of \(2^8\) nonequivalent propositions over \(U\text{.}\)

3.6.3.5.

Answer.
Two possible answers: \(s\) is odd and \((s-1)(s-3)(s-5)(s-7)=0\)

3.6.3.7.

Solution.
\(b\) and \(c\)

3.7 Mathematical Induction
3.7.4 Exercises

3.7.4.1.

Answer.
We wish to prove that \(P(n):1+3+5+\cdots +(2n-1)=n^2\) is true for \(n \geqslant 1\text{.}\) Recall that the \(n\)th odd positive integer is \(2n - 1\text{.}\)
Basis: for \(n=1\text{,}\) \(P(n)\) is \(1=1^2\text{,}\) which is true
Induction: Assume that for some \(n\geqslant 1\text{,}\) \(P(n)\) is true. Then we infer that \(P(n+1)\) follows:
\begin{equation*} \begin{split} 1+3+\cdots +(2(n+1)-1) &= (1+3+\cdots +(2n-1) ) +(2(n+1)-1)\\ & =n^2+(2n+1) \quad \textrm{by } P(n) \textrm{ and basic algebra}\\ & =(n+1)^2 \quad \blacksquare \end{split} \end{equation*}

3.7.4.3.

Answer.
Proof:
  • Basis: We note that the proposition is true when \(n=1\text{:}\) \(\sum_{k=1}^{1} k^2 =1= \frac{1(2)(3)}{6}\text{.}\)
  • Induction: Assume that the proposition is true for some \(n \geq 1\text{.}\) This is the induction hypothesis.
    \begin{equation*} \begin{split} \sum_{k=1}^{n+1} k^2 &=\sum_{k=1}^n k^2+(n+1)^2\\ &=\frac{n(n+1)(2n+1)}{6}+(n+1)^2 \qquad \textrm{by the induction hypothesis} \\ &=\frac{(n+1)(2n^2+7n+6)}{6}\\ &=\frac{(n+1)(n+2)(2n+3)}{6}\qquad \blacksquare \end{split} \end{equation*}
    Therefore, the truth of the proposition for \(n\) implies the truth of the proposition for \(n+1\text{.}\)

3.7.4.5.

Solution.
Basis: For \(n=1\text{,}\) we observe that \(\frac{1}{(1\cdot 2)}=\frac{1}{(1+1)}\)
Induction: Assume that for some \(n\geqslant 1\text{,}\) the formula is true.
Then:
\begin{equation*} \begin{split} \frac{1}{(1\cdot 2)}+\cdots +\frac{1}{n(n+1)} +\frac{1}{(n+1)(n+2)} &=\frac{n}{n+1}+\frac{1}{(n+1)(n+2)}\\ &=\frac{(n+2)n}{(n+1)(n+2)}+\frac{1}{(n+1)(n+2)}\\ &=\frac{(n+1)^2}{(n+1)(n+2)}\\ &=\frac{n+1}{n+2} \quad \blacksquare\\ \end{split} \end{equation*}

3.7.4.7.

Answer.
Let \(A_n\) be the set of strings of zeros and ones of length \(n\) (we assume that \(\lvert A_n \rvert =2^n\) is known). Let \(E_n\) be the set of the “even” strings, and \(E_{n}^{c}=\) the odd strings. The problem is to prove that for \(n\geqslant 1\text{,}\) \(\lvert E_n \rvert =2^{n-1}\text{.}\) Clearly, \(\lvert E_1\rvert =1\text{,}\) and, if for some \(n\geqslant 1, \lvert E_n\rvert =2^{n-1}\text{,}\) it follows that \(\lvert E_{n+1}\rvert =2^n\) by the following reasoning.
We partition \(E_{n+1}\) according to the first bit: \(E_{n+1}=\{1s\mid s \in E_n^c \}\cup \{ 0s \mid s \in E_n\}\)
Since \(\{1s\mid s \in E_n^c\}\) and \(\{0s \mid s \in E_n\}\) are disjoint, we can apply the addition law. Therefore,
\begin{equation*} \begin{split} \quad \lvert E_{n+1}\rvert & =\lvert E_n^c \rvert +\lvert E_n \rvert \\ & =2^{n-1}+ (2^n-2^{n-1}) =2^n.\quad \blacksquare \end{split} \end{equation*}

3.7.4.9.

Solution.
Assume that for \(n\) persons \((n\geqslant 1),\frac{(n-1)n}{2}\) handshakes take place. If one more person enters the room, he or she will shake hands with \(n\) people,
\begin{equation*} \begin{split} \frac{(n-1)n}{2}+n & =\frac{n^2-n+2n}{2}\\ &=\frac{n^2+n}{2}=\frac{n(n+1)}{2}\\ &=\frac{((n+1)-1)(n+1)}{2} \blacksquare \end{split} \end{equation*}
Also, for \(n=1\text{,}\) there are no handshakes, which matches the conjectured formula:
\begin{equation*} \frac{(1-1)(1)}{2}=0 \quad \blacksquare. \end{equation*}

3.7.4.11.

Solution.
Let \(p(n)\) be “\(a_{1} + a_2 + \cdots + a_n\) has the same value no matter how it is evaluated.”
Basis: \(a_1 + a_2 + a_3\) may be evaluated only two ways. Since + is associative, \((a_1 + a_2) + a_3 = a_1 + (a_2 + a_3)\text{.}\) Hence, \(p(3)\) is true.
Induction: Assume that for some \(n\geq 3\text{,}\) \(p(3), p(4), \dots , p(n)\) are all true. Now consider the sum \(a_1 + a_2 + \cdots + a_n + a_{n+1}\text{.}\) Any of the \(n\) additions in this expression can be applied last. If the \(j\)th addition is applied last, we have \(c_j=(a_1+a_2+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\text{.}\) No matter how the expression to the left and right of the \(j^{\text{th}}\) addition are evaluated, the result will always be the same by the induction hypothesis, specifically \(p(j)\) and \(p(n+1-j)\text{.}\) We now can prove that \(c_1=c_2=\cdots =c_n\text{.}\) If \(i < j\text{,}\)
\begin{equation*} \begin{split} c_i &=(a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_{n+1})\\ &=(a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\\ &=((a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_j))+(a_{j+1}+\cdots +a_{n+1})\\ &=(a_1+a_2+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\\ &=c_j \quad\quad \blacksquare \end{split} \end{equation*}

3.7.4.12.

Hint.
The number of times the rules are applied should be the integer that you do the induction on.

3.7.4.13.

Hint.
Let \(p(m)\) be the proposition that \(x^{m+n}= x^mx^n\) for all \(n\geq 1\text{.}\)
Solution.
For \(m\geqslant 1\text{,}\) let \(p(m)\textrm{ be } x^{n+m}=x^nx^m\) for all \(n\geqslant 1\text{.}\) The basis for this proof follows directly from the basis for the definition of exponentiation.
Induction: Assume that for some \(m\geq 1\text{,}\) \(p(m)\) is true. Then
\begin{equation*} \begin{split} x^{n+(m+1)} & =x^{(n+m)+1}\quad \textrm{by associativity of integer addition}\\ &=x^{n+m}x^1 \quad \textrm{ by recursive definition}\\ &=x^nx^mx^1 \quad \textrm{induction hypothesis}\\ &=x^nx^{m+1}\quad \textrm{recursive definition}\quad \blacksquare\\ \end{split} \end{equation*}

3.8 Quantifiers
3.8.5 Exercises

3.8.5.1.

Answer.
  1. \(\displaystyle (\forall x)(F(x)\to C(x))\)
  2. There are objects in the sea which are not fish.
  3. Every fish lives in the sea.

3.8.5.3.

Answer.
  1. There is a book with a cover that is not blue.
  2. Every mathematics book that is published in the United States has a blue cover.
  3. There exists a mathematics book with a cover that is not blue.
  4. There exists a book that appears in the bibliography of every mathematics book.
  5. \(\displaystyle (\forall x)(B(x)\to M(x))\)
  6. \(\displaystyle (\exists x)(M(x)\land \neg U(x))\)
  7. \(\displaystyle (\exists x)((\forall y)(\neg R(x,y))\)

3.8.5.5.

Answer.
The equation \(4u^2-9=0\) has a solution in the integers. (False)

3.8.5.7.

Answer.
  1. Every subset of \(U\) has a cardinality different from its complement. (True)
  2. There is a pair of disjoint subsets of \(U\) both having cardinality 5. (False)
  3. \(A-B=B^c-A^c\) is a tautology. (True)

3.8.5.9.

Answer.
\((\forall a)_{\mathbb{Q}}(\forall b)_{\mathbb{Q}}\)(\(a+b\) is a rational number.)

3.8.5.10.

Hint.
You will need three quantifiers.

3.8.5.11.

Answer.
Let \(I=\{1,2,3,\ldots ,n\}\)
  1. \(\displaystyle (\exists x)_I\left(x\in A_i\right)\)
  2. \(\displaystyle (\forall x)_I\left(x\in A_i\right)\)

3.9 A Review of Methods of Proof
3.9.3 Exercises

3.9.3.1.

Answer.
The given statement can be written in if \(\dots\) , then \(\dots\) format as: If \(x\) and \(y\) are two odd positive integers, then \(x+y\) is an even integer.
Proof: Assume \(x\) and \(y\) are two positive odd integers. It can be shown that \(x+y=2 \cdot \textrm{(some positive integer)}\text{.}\)
\(x\) odd and positive \(\Rightarrow x=2m+1\) for some \(m \geq 0\text{,}\)
\(y\) odd and positive \(\Rightarrow y=2n+1\) for some \(n \geq 0\text{.}\)
Then,
\begin{equation*} x+y=(2m+1)+(2n+1)=2((m+n)+1)=2\cdot\textrm{(some positive integer)} \end{equation*}
Therefore, \(x+y\) is an even positive integer. \(\square\)

3.9.3.3.

Answer.
Proof: (Indirect) Assume to the contrary, that \(\sqrt{2}\) is a rational number. Then there exists \(p,q\in \mathbb{Z}, (q\neq 0)\) where \(\frac{p}{q}=\sqrt{2}\) and where \(\frac{p}{q}\) is in lowest terms, that is, \(p\) and \(q\) have no common factor other than 1.
\begin{equation*} \begin{split} \frac{p}{q}=\sqrt{2} & \Rightarrow \frac{p^2}{q^2}=2\\ &\Rightarrow p^2=2 q^2 \\ &\Rightarrow p^2 \textrm{ is an even integer}\\ &\Rightarrow p \textrm{ is an even integer (see Exercise 2)}\\ &\Rightarrow \textrm{4 is a factor of }p^2\\ &\Rightarrow q^2 \textrm{ is even}\\ &\Rightarrow q \textrm{ is even}\\ \end{split} \end{equation*}
Hence both \(p\) and \(q\) have a common factor, namely 2, which is a contradiction. \(\square\)

3.9.3.5.

Answer.
Proof: (Indirect) Assume \(x,y\in \mathbb{R}\) and \(x+y\leqslant 1\text{.}\) Assume to the contrary that \(\left(x\leqslant \frac{1}{2}\textrm{ or } y\leqslant \frac{1}{2}\right)\) is false, which is equivalent to \(x>\frac{1}{2}\textrm{ and } y>\frac{1}{2}\text{.}\) Hence \(x+y>\frac{1}{2}+\frac{1}{2}=1\text{.}\) This contradicts the assumption that \(x+y\leqslant 1\text{.}\) \(\square\)

4 More on Sets
4.1 Methods of Proof for Sets
4.1.5 Exercises

4.1.5.1.

Answer.
  1. Assume that \(x\in A\) (condition of the conditional conclusion \(A \subseteq C\)). Since \(A \subseteq B\text{,}\) \(x\in B\) by the definition of \(\subseteq\text{.}\) \(B\subseteq C\) and \(x\in B\) implies that \(x\in C\text{.}\) Therefore, if \(x\in A\text{,}\) then \(x\in C\text{.}\) \(\square\)
  2. (Proof that \(A -B \subseteq A\cap B^c\)) Let \(x\) be in \(A - B\text{.}\) Therefore, x is in \(A\text{,}\) but it is not in B; that is,\(\text{ }x \in A\) and \(x \in B^c \Rightarrow x\in A\cap B^c\text{.}\) \(\square\)
  3. \((\Rightarrow )\)Assume that \(A \subseteq B\) and \(A \subseteq C\text{.}\) Let \(x\in A\text{.}\) By the two premises,\(x\in B\) and \(x\in C\text{.}\) Therefore, by the definition of intersection, \(x\in B\cap C\text{.}\) \(\square\)
  4. \((\Rightarrow )\)(Indirect) Assume that \(B^c\) is not a subset of \(A^c\) . Therefore, there exists \(x\in B^c\) that does not belong to \(A^c\text{.}\) \(x \notin A^c \Rightarrow x \in A\text{.}\) Therefore, \(x\in A\) and \(x\notin B\text{,}\) a contradiction to the assumption that \(A\subseteq B\text{.}\) \(\square\)
  5. There are two cases to consider. The first is when \(C\) is empty. Then the conclusion follows since both Cartesian products are empty.
    If \(C\) isn’t empty, we have two subcases, if \(A\) is empty, \(A\times C = \emptyset\text{,}\) which is a subset of every set. Finally, the interesting subcase is when \(A\) is not empty. Now we pick any pair \((a,c) \in A\times C\text{.}\) This means that \(a\) is in \(A\) and \(c\) is in \(C\text{.}\) Since \(A\) is a subset of \(B\text{,}\) \(a\) is in \(B\) and so \((a,c) \in B \times C\text{.}\) Therefore \(A\times C \subseteq B\times C\text{.}\) \(\square\)

4.1.5.3.

Answer.
  1. If \(A = \mathbb{Z}\) and \(B=\emptyset\text{,}\) \(A - B = \pmb{\mathbb{Z}}\text{,}\) while \(B - A = \emptyset\text{.}\)
  2. If \(A=\{0\}\) and \(B = \{1\}\text{,}\) \((0,1) \in A \times B\text{,}\) but \((0, 1)\) is not in \(B\times A\text{.}\)
  3. Let \(A = \emptyset\text{,}\) \(B = \{0\}\text{,}\) and \(C = \{1\}\text{.}\)
  4. If \(A = \{1\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\emptyset\text{,}\) then the left hand side of the identity is \(\{1\}\) while the right hand side is the empty set. Another example is \(A = \{1,2\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\{2\}.\)

4.1.5.5.

Solution.
Proof: Let \(p(n)\) be
\begin{equation*} A\cap (B_1\cup B_2\cup \cdots \cup B_n)=(A\cap B_1)\cup (A\cap B_2)\cup \cdots \cup (A\cap B_n)\text{.} \end{equation*}
Basis: We must show that \(p(2) : A \cap (B_1 \cup B_2 )=(A\cap B_1) \cup (A\cap B_2)\) is true. This was done by several methods in section 4.1.
Induction: Assume for some \(n\geq 2\) that \(p(n)\) is true. Then
\begin{equation*} \begin{split} A\cap (B_1\cup B_2\cup \cdots \cup B_{n+1})&=A\cap ((B_1\cup B_2\cup \cdots \cup B_n)\cup B_{n+1})\\ &=(A \cap (B_1\cup B_2\cup \cdots \cup B_n))\cup (A\cap B_{n+1}) \quad \textrm{by } p(2)\\ &=((A\cap B_1)\cup \cdots \cup (A\cap B_n))\cup (A\cap B_{n+1})\quad \textrm{by the induction hypothesis}\\ &=(A\cap B_1)\cup \cdots \cup (A\cap B_n)\cup (A\cap B_{n+1})\quad \square\\ \end{split} \end{equation*}

4.1.5.6.

Answer.
The statement is false. The sets \(A=\{1,2\}\text{,}\) \(B=\{2,3\}\) and \(C=\{3,4\}\) provide a counterexample. Looking ahead to Chapter 6, we would say that the relation of being non-disjoint is not transitive 6.3.3

4.2 Laws of Set Theory
4.2.4 Exercises

4.2.4.1.

Answer.
  2. \begin{equation*} \begin{array}{ccccccc} A & B &A^c & B^c & A\cup B & (A\cup B)^c &A^c\cap B^c \\ \hline 0 & 0 &1 & 1 & 0 & 1 & 1 \\ 0 & 1 &1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ \end{array} \end{equation*}
    The last two columns are the same so the two sets must be equal.
  3. \begin{equation*} \begin{split} x\in A\cup A & \Rightarrow (x\in A) \lor (x\in A)\quad\textrm{by the definition of } \cap\\ &\Rightarrow x\in A \quad\textrm{ by the idempotent law of logic} \end{split} \end{equation*}
    Therefore, \(A\cup A\subseteq A\text{.}\)
    \begin{equation*} \begin{split} x\in A &\Rightarrow (x\in A) \lor (x\in A) \quad \textrm{ by conjunctive addition}\\ & \Rightarrow x\in A\cup A\\ \end{split} \end{equation*}
    Therefore, \(A \subseteq A\cup A\) and so we have \(A\cup A=A\text{.}\)

4.2.4.3.

Answer.
For all parts of this exercise, a reason should be supplied for each step. We have supplied reasons only for part a and left them out of the other parts to give you further practice.
  1. \begin{equation*} \begin{split} A \cup (B-A)&=A\cup (B \cap A^c) \textrm{ by Exercise 1 of Section 4.1}\\ & =(A\cup B)\cap (A\cup A^c) \textrm{ by the distributive law}\\ &=(A\cup B)\cap U \textrm{ by the null law}\\ &=(A\cup B) \textrm{ by the identity law } \square \end{split}\text{.} \end{equation*}
  2. \begin{equation*} \begin{split} A - B & = A \cap B ^c\\ & =B^c\cap A\\ &=B^c\cap (A^c)^c\\ &=B^c-A^c\\ \end{split}\text{.} \end{equation*}
  3. Select any element, \(x \in A\cap C\text{.}\) One such element exists since \(A\cap C\) is not empty.
    \begin{equation*} \begin{split} x\in A\cap C\ &\Rightarrow x\in A \land x\in C \\ & \Rightarrow x\in B \land x\in C \\ & \Rightarrow x\in B\cap C \\ & \Rightarrow B\cap C \neq \emptyset \quad \square \\ \end{split}\text{.} \end{equation*}
    Therefore,
  4. \begin{equation*} \begin{split} A\cap (B-C) &=A\cap (B\cap C^c) \\ & = (A\cap B\cap A^c)\cup (A\cap B\cap C^c) \\ & =(A\cap B)\cap (A^c\cup C^c) \\ & =(A\cap B)\cap (A\cup C)^c \\ & =(A-B)\cap (A-C) \quad \square\\ \end{split}\text{.} \end{equation*}
  5. \begin{equation*} \begin{split} A-(B\cup C)& = A\cap (B\cup C)^c\\ & =A\cap (B^c\cap C^c)\\ & =(A\cap B^c)\cap (A\cap C^c)\\ & =(A-B)\cap (A-C) \quad \square\\ \end{split}\text{.} \end{equation*}

4.2.4.5. Hierarchy of Set Operations.

Answer.
  1. \(\displaystyle A\cup ((B^c)\cap C)\)
  2. \(\displaystyle (A\cap B)\cup (C\cap B)\)
  3. \(\displaystyle (A\cup B)\cup (C^c)\)

4.3 Minsets
4.3.3 Exercises

4.3.3.1.

Answer.
  1. \(\displaystyle \{1\}, \{2, 3, 4, 5\}, \{6\}, \{7, 8\}, \{9, 10\}\)
  2. \(2^5\) , as compared with \(2^{10}\text{.}\) \(\{1, 2\}\) is one of the 992 sets that can’t be generated.

4.3.3.3.

Answer.
\(B_1= \{00, 01, 10, 11\}\) and \(B_2 = \{0, 00, 01\}\) generate minsets \(\{00, 01\}, \{0\}, \{10, 11\}\text{,}\) and \(\{\lambda , 1\}\text{.}\) Note: \(\lambda\) is the null string, which has length zero.

4.3.3.5.

Answer.
  1. \(B_1\cap B_2=\emptyset\text{,}\) \(B_1\cap B_2^c=\{0,2,4\}\text{,}\) \(B_1^c\cap B_2=\{1,5\}\text{,}\) \(B_1^c\cap B_2^c=\{3\}\)
  2. \(2^3\text{,}\) since there are 3 nonempty minsets.

4.3.3.7.

Answer.
Let \(a\in A\text{.}\) For each \(i\text{,}\) \(a\in B_i\text{,}\) or \(a\in B_i{}^c\text{,}\) since \(B_i\cup B_i{}^c=A\) by the complement law. Let \(D_i=B_i\) if \(a\in B_i\text{,}\) and \(D_i=B_i{}^c\) otherwise. Since \(a\) is in each \(D_i\text{,}\) it must be in the minset \(D_1\cap D_2 \cdots \cap D_n\text{.}\) Now consider two different minsets \(M_1= D_1\cap D_2\cdots \cap D_n\text{,}\) and \(M_2=G_1\cap G_2\cdots \cap G_n\text{,}\) where each \(D_i\) and \(G_i\) is either \(B_i\) or \(B_i{}^c\text{.}\) Since these minsets are not equal, \(D_i\neq G_i\text{,}\) for some \(i\text{.}\) Therefore, \(M_1\cap M_2=D_1\cap D_2 \cdots \cap D_n\cap G_1\cap G_2\cdots \cap G_n=\emptyset\text{,}\) since two of the sets in the intersection are disjoint. Since every element of \(A\) is in a minset and the minsets are disjoint, the nonempty minsets must form a partition of \(A\text{.}\) \(\square\)

4.4 The Duality Principle
4.4.2 Exercises

4.4.2.1.

Answer.
  1. \(\displaystyle A\cap (B\cup A)=A\)
  2. \(\displaystyle A \cap \left(\left(B^c\cap A\right)\cup B\right)^c=\emptyset\)
  3. \(\displaystyle \left(A\cap B^c\right)^c\cup B=A^c\cup B\)

4.4.2.3.

Answer.
  1. \(\displaystyle p \land \neg ((\neg q \land p)\lor q) \Leftrightarrow 0\)
  2. \(\displaystyle (\neg (p \lor (\neg q))\land q) \Leftrightarrow ((\neg p) \land q)\)

4.4.2.5.

Answer.
The maxsets are:
  • \(\displaystyle B_1\cup B_2=\{1,2,3,5\}\)
  • \(\displaystyle B_1\cup B_2{}^c=\{1,3,4,5,6\}\)
  • \(\displaystyle B_1{}^c\cup B_2=\{1,2,3,4,6\}\)
  • \(\displaystyle B_1{}^c\cup B_2{}^c=\{2,4,5,6\}\)
They do not form a partition of \(A\) since it is not true that the intersection of any two of them is empty. A set is said to be in maxset normal form when it is expressed as the intersection of distinct nonempty maxsets or it is the universal set \(U\text{.}\)

5 Introduction to Matrix Algebra
5.1 Basic Definitions and Operations
5.1.4 Exercises

5.1.4.1.

Answer.
For parts c, d and i of this exercise, only a verification is needed. Here, we supply the result that will appear on both sides of the equality.
  1. \(\displaystyle AB=\left( \begin{array}{cc} -3 &6 \\ 9 & -13 \\ \end{array} \right) \quad BA=\left( \begin{array}{cc} 2 & 3 \\ -7 & -18 \\ \end{array} \right)\)
  2. \(\displaystyle \left( \begin{array}{cc} 1 & 0 \\ 5 & -2 \\ \end{array} \right)\)
  3. \(\displaystyle \left( \begin{array}{cc} 3 & 0 \\ 15 & -6 \\ \end{array} \right)\)
  4. \(\displaystyle \left( \begin{array}{ccc} 18 & -15 & 15 \\ -39 & 35 & -35 \\ \end{array} \right)\)
  5. \(\displaystyle \left( \begin{array}{ccc} -12 & 7 & -7 \\ 21 & -6 & 6 \\ \end{array} \right)\)
  6. \(\displaystyle B+0=B\)
  7. \(\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)\)
  8. \(\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)\)
  9. \(\displaystyle \left( \begin{array}{cc} 5 & -5 \\ 10 & 15 \\ \end{array} \right)\)

5.1.4.3.

Answer.
\(\left( \begin{array}{cc} 1/2 & 0 \\ 0 & 1/3 \\ \end{array} \right)\)

5.1.4.5.

Answer.
\(A^3=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 8 & 0 \\ 0 & 0 & 27 \\ \end{array} \right)\) \(A^{15}=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 32768 & 0 \\ 0 & 0 & 14348907 \\ \end{array} \right)\)

5.1.4.7.

Answer.
  1. \(Ax=\left( \begin{array}{c} 2x_1+1x_2 \\ 1x_1-1x_2 \\ \end{array} \right)\) equals \(\left( \begin{array}{c} 3 \\ 1 \\ \end{array} \right)\) if and only if both of the equalities \(2x_1+x_2=3 \textrm{ and } x_1-x_2=1\) are true.
  2. (i) \(A=\left( \begin{array}{cc} 2 & -1 \\ 1 & 1 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 4 \\ 0 \\ \end{array} \right)\)
  3. \(A=\left( \begin{array}{ccc} 1 & 1 & 2 \\ 1 & 2 & -1 \\ 1 & 3 & 1 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 1 \\ -1 \\ 5 \\ \end{array} \right)\)
  4. \(A=\left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 3 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 3 \\ 5 \\ 6 \\ \end{array} \right)\)

5.2 Special Types of Matrices
5.2.3 Exercises

5.2.3.1.

Answer.
  1. \(\displaystyle \left( \begin{array}{cc} -1/5 & 3/5 \\ 2/5 & -1/5 \\ \end{array} \right)\)
  2. No inverse exists.
  3. \(\displaystyle \left( \begin{array}{cc} 1 & 3 \\ 0 & 1 \\ \end{array} \right)\)
  4. \(\displaystyle A^{-1}=A\)
  5. \(\displaystyle \left( \begin{array}{ccc} 1/3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -1/5 \\ \end{array} \right)\)

5.2.3.3.

Answer.
Let A and B be \(n\) by \(n\) invertible matrices.
\begin{equation*} \begin{split} \left(B^{-1}A^{-1}\right)(AB)&=\left(B^{-1}\right)\left(A^{-1}(AB)\right)\\ &= \left(B^{-1}\right) \left(\left(A^{-1} A\right) B\right)\\ &=(\left(B^{-1}\right)I B )\\ &=B^{-1}(B)\\ &=I \end{split} \end{equation*}
Similarly, \((AB)\left(B^{-1}A^{-1}\right)=I\text{.}\)
By Theorem 5.2.6, \(B^{-1}A^{-1}\) is the only inverse of \(AB\text{.}\) If we tried to invert \(AB\) with \(A^{-1}B^{-1}\text{,}\) we would be unsuccessful since we cannot rearrange the order of the matrices.

5.2.3.5. Linearity of Determinants.

Solution.
  1. Let \(A=\left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right)\) and \(B=\left( \begin{array}{cc} x & y \\ z & w \\ \end{array} \right)\text{.}\)
    \begin{equation*} \begin{split} \det(A B) & =\det \left( \begin{array}{cc} a x+b z & a y+b w \\ c x+d z & c y+d w \\ \end{array} \right)\\ &=a d w x-a d y z-b c w x+b c y z \quad \text{four terms cancel}\\ &=(ad-bc)x w - (ad -bc)y z\\ &=(ad-bc)(x w - y z)\\ &=(\det A)(\det B) \end{split}\text{.} \end{equation*}
  2. \(1=\det I=\det \left(AA^{-1}\right)=\det A\text{ }\det A^{-1}\text{.}\) Now solve for \(\det A^{-1}\text{.}\)
  3. \(\det A=1\cdot 1 - 3 \cdot 2 =-5\) while \(\det A^{-1}= \frac{1}{5} \cdot \frac{1}{5} - \frac{3}{5} \cdot \frac{2}{5} = -\frac{1}{5}\text{.}\)

5.2.3.7.

Answer.
Basis: \((n=1): \det A^1=\det A =(\det A )^1\)
Induction: Assume \(\det(A^n)=(\det A)^n\) for some \(n\geq 1\text{.}\)
\begin{equation*} \begin{split} \det A^{n+1} & =\det \left(A^nA\right)\quad \textrm{ by the definition of exponents}\\ &=\det \left(A^n\right)\det (A)\quad \textrm{ by exercise 5} \\ &=(det A)^n(\det A)\quad \textrm{ by the induction hypothesis }\\ &=(\det A)^{n+1} \end{split} \end{equation*}

5.2.3.9.

Answer.
  1. Assume \(A=B D B^{-1}\)
    Basis: \((m=1\)): \(A^{1}=A=B D^1 B^{-1} \) is given.
    Induction: Assume that for some positive integer \(m\text{,}\) \(A^m=BD^mB^{-1}\)
    \begin{equation*} \begin{split} A^{m+1} &=A^mA\\ &=(B D^m B^{-1})(BDB^{-1})\quad \textrm{ by the induction hypothesis} \\ &=(BD^m(B^{-1} B ) (DB^{-1}) \quad \textrm{ by associativity} \\ &=B D^m D B^{-1} \quad \textrm{ by the definition of inverse}\\ &=B D^{m+1} B^{-1} \quad \square \end{split} \end{equation*}
  2. \(\displaystyle A^{10}=BD^{10}B^{-1}= \left( \begin{array}{cc} -9206 & 15345 \\ -6138 & 10231 \\ \end{array} \right)\)

5.3 Laws of Matrix Algebra
5.3.3 Exercises

5.3.3.1.

Answer.
  1. Let \(A\) and \(B\) be \(m\) by \(n\) matrices. Then \(A+B=B+A\text{,}\)
  2. Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m\) by \(n\) matrices. Then \(A+(B+C)=(A+B)+C\text{.}\)
  3. Let \(A\) and \(B\) be \(m\) by \(n\) matrices, and let \(c\in \mathbb{R}\text{.}\) Then \(c(A+B)=cA+cB\text{,}\)
  4. Let \(A\) be an \(m\) by \(n\) matrix, and let \(c_1,c_2\in \mathbb{R}\text{.}\) Then \(\left(c_1+c_2\right)A=c_1A+c_2A\text{.}\)
  5. Let \(A\) be an \(m\) by \(n\) matrix, and let \(c_1,c_2\in \mathbb{R}\text{.}\) Then \(c_1\left(c_2A\right)=\left(c_1c_2\right)A\)
  6. Let \(\pmb{0}\) be the zero matrix, of size \(m \textrm{ by } n\text{,}\) and let \(A\) be a matrix of size \(n \textrm{ by } r\text{.}\) Then \(\pmb{0}A=\pmb{0}=\textrm{ the } m \textrm{ by } r \textrm{ zero matrix}\text{.}\)
  7. Let \(A\) be an \(m \textrm{ by } n\) matrix, and \(0 = \textrm{ the number zero}\text{.}\) Then \(0A=0=\textrm{ the } m \textrm{ by } n \textrm{ zero matrix}\text{.}\)
  8. Let \(A\) be an \(m \textrm{ by } n\) matrix, and let \(\pmb{0}\) be the \(m \textrm{ by } n\) zero matrix. Then \(A+\pmb{0}=A\text{.}\)
  9. Let \(A\) be an \(m \textrm{ by } n\) matrix. Then \(A+(- 1)A=\pmb{0}\text{,}\) where \(\pmb{0}\) is the \(m \textrm{ by } n\) zero matrix.
  10. Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(n \textrm{ by } r\text{,}\) and \(n \textrm{ by } r\) matrices respectively. Then \(A(B+C)=AB+AC\text{.}\)
  11. Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(r \textrm{ by } m\text{,}\) and \(r \textrm{ by } m\) matrices respectively. Then \((B+C)A=BA+CA\text{.}\)
  12. Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(n \textrm{ by } r\text{,}\) and \(r \textrm{ by } p\) matrices respectively. Then \(A(BC)=(AB)C\text{.}\)
  13. Let \(A\) be an \(m \textrm{ by } n\) matrix, \(I_m\) the \(m \textrm{ by } m\) identity matrix, and \(I_n\) the \(n \textrm{ by } n\) identity matrix. Then \(I_mA=AI_n=A\)
  14. Let \(A\) be an \(n \textrm{ by } n\) matrix. Then if \(A^{-1}\) exists, \(\left(A^{-1}\right)^{-1}=A\text{.}\)
  15. Let \(A\) and \(B\) be \(n \textrm{ by } n\) matrices. Then if \(A^{-1}\) and \(B^{-1}\) exist, \((AB)^{-1}=B^{-1}A^{-1}\text{.}\)

5.3.3.3.

Answer.
  1. \(\displaystyle AB+AC=\left( \begin{array}{ccc} 21 & 5 & 22 \\ -9 & 0 & -6 \\ \end{array} \right)\)
  2. \(\displaystyle A^{-1}=\left( \begin{array}{cc} 1 & 2 \\ 0 & -1 \\ \end{array} \right)=A\)
  3. \(A(B+C)=A B+ B C\text{,}\) which is given in part (a).
  4. \(\left(A^2\right)^{-1}=(AA)^{-1}=(A^{-1}A)=I^{-1}=I \quad \) by part c

5.4 Matrix Oddities
5.4.2 Exercises

5.4.2.1.

Answer.
In elementary algebra (the algebra of real numbers), each of the given oddities does not exist.
  1. \(AB\) may be different from \(BA\text{.}\) Not so in elementary algebra, since \(a b = b a\) by the commutative law of multiplication.
  2. There exist matrices \(A\) and \(B\) such that \(AB = \pmb{0}\text{,}\) yet \(A\neq \pmb{0}\)and \(B\neq \pmb{0}\text{.}\) In elementary algebra, the only way \(ab = 0\) is if either \(a\) or \(b\) is zero. There are no exceptions.
  3. There exist matrices \(A\text{,}\) \(A\neq \pmb{0}\text{,}\) yet \(A^2=\pmb{0}\text{.}\) In elementary algebra, \(a^2=0\Leftrightarrow a=0\text{.}\)
  4. There exist matrices \(A^2=A\text{.}\) where \(A\neq \pmb{0}\) and \(A\neq I\text{.}\) In elementary algebra, \(a^2=a\Leftrightarrow a=0 \textrm{ or } 1\text{.}\)
  5. There exist matrices \(A\) where \(A^2=I\) but \(A\neq I\) and \(A\neq -I\text{.}\) In elementary algebra, \(a^2=1\Leftrightarrow a=1\textrm{ or }-1\text{.}\)

5.4.2.3.

Answer.
  1. \(\det A \neq 0\Rightarrow A^{-1}\) exists, and if you multiply the equation \(A^2=A\) on both sides by \(A^{-1}\) , you obtain \(A=I\text{.}\)
  2. Counterexample: \(A=\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \\ \end{array} \right)\)

5.4.2.5.

Answer.
  1. \(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=4/3\text{,}\) and \(x_2=1/3\)
  2. \(A^{-1}=\left( \begin{array}{cc} 1 & -1 \\ 1 & -2 \\ \end{array} \right)\) \(x_1=4\text{,}\) and \(x_2=4\)
  3. \(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=2/3\text{,}\) and \(x_2=-1/3\)
  4. \(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=0\text{,}\) and \(x_2=1\)
  5. The matrix of coefficients for this system has a zero determinant; therefore, it has no inverse. The system cannot be solved by this method. In fact, the system has no solution.

6 Relations
6.1 Basic Definitions
6.1.4 Exercises

6.1.4.1.

Answer.
  1. \(\displaystyle (2,4), (2,8)\)
  2. \(\displaystyle (2, 3), (2, 4), (5,8)\)
  3. \(\displaystyle (1,1), (2,4)\)

6.1.4.3.

Answer.
  1. \(\displaystyle r=\{(1,2), (2,3), (3,4), (4,5)\}\)
  2. \(\displaystyle r^2 = \{(1,3), (2,4), (3,5)\}=\{(x,y) : y=x+2, x,y\in A\}\)
  3. \(\displaystyle r^3=\{(1,4), (2,5)\}=\{(x,y) : y=x+3, x,y \in A\}\)

6.1.4.5.

Answer.
  1. When \(n=3\text{,}\) there are 27 pairs in the relation.
  2. Imagine building a pair of disjoint subsets of \(S\text{.}\) For each element of \(S\) there are three places that it can go: into the first set of the ordered pair, into the second set, or into neither set. Therefore the number of pairs in the relation is \(3^n\text{,}\) by the product rule.

6.1.4.7.

Solution.
Assume \((x,y)\in r_1r_3\text{.}\) This implies that there exist \(z \in A\) such that \((x,z)\in r_1\) and \((z,y)\in r_3\text{.}\) We are given that \(r_1\subseteq r_2\text{,}\) which implies that \((x,z)\in r_2\text{.}\) Combining this with \((z,y)\in r_3\) implies that \((x,y)\in r_2r_3\text{,}\) which proves that \(r_1r_3\subseteq r_2r_3\text{.}\)

6.2 Graphs of Relations on a Set
6.2.2 Exercises

6.2.2.1.

Answer.
described in detail following the image
Digraph for \(\leq\)
Figure 6.2.7. Digraph for exercise 1

6.2.2.3.

Answer.
See Figure 6.2.8
Figure 6.2.8. Digraph of the relation \(t\)

6.3 Properties of Relations
6.3.4 Exercises

6.3.4.1.

Answer.
  1. “Divides” is reflexive because, if \(i\) is any positive integer, \(i\cdot 1 = i\) and so \(i \mid i\)
  2. “Divides” is antisymmetric. Suppose \(i\) and \(j\) are two distinct positive integers. One of them has to be less than the other, so we will assume \(i \lt j\text{.}\) If \(i \mid j\text{,}\) then for some positive integer \(k\text{,}\) where \(k \ge 1\) we have \(i \cdot k = j\text{.}\) But this means that \(j \cdot \frac{1}{k}=i\) and since \(\frac{1}{k}\) is not a positive integer, \(j \nmid i\text{.}\)
  3. “Divides” is transitive. If \(h\text{,}\) \(i\) and \(j\) are positive integers such that \(h \mid i\) and \(i \mid j\text{,}\) there must be two positive integers \(k_1\) and \(k_2\) such that \(h \cdot k_1 =i\) and \(i \cdot k_2 = j\text{.}\) Combining these equalities we get \(h \cdot (k_1 \cdot k_2) = j\) and so \(h \mid j\text{.}\)

6.3.4.3.

Answer.
Table 6.3.19. Properties of relations defined by digraphs
Part reflexive? symmetric? antisymmetric? transitive?
i yes no no yes
ii yes no yes yes
iii no no no no
iv no yes yes yes
v yes yes no yes
vi yes no yes yes
vii no no no no
  1. See Table 6.3.19
  2. Graphs ii and vi show partial ordering relations. Graph v is of an equivalence relation.

6.3.4.5.

Answer.
  1. No, since \(\mid 1-1\mid =0\neq 2\text{,}\) for example
  2. Yes, because \(\mid i-j\mid =\)\(\mid j-i\mid \text{.}\)
  3. No, since \(\mid 2-4\mid =2\) and \(\mid 4-6\mid =2\text{,}\) but \(\mid 2-6\mid =4\neq 2\text{,}\) for example.
  4. See Figure 6.3.20
described in detail following the image
Solution to number 5c of section 6.3
Figure 6.3.20.

6.3.4.7.

Answer.
Let \(a\) be any element of \(A\text{.}\) \(a\in [a]\) since \(r\) is reflexive, so each element of \(A\) is in some equivalence class. Therefore, the union of all equivalence classes equals \(A\text{.}\) Next we show that any two equivalence classes are either identical or disjoint and we are done. Let \([a]\) and \([b]\) be two equivalence classes, and assume that \([a]\cap [b]\neq \emptyset\text{.}\) We want to show that \([a]=[b]\text{.}\) To show that \([a]\subseteq [b]\text{,}\) let \(x\in [a]\text{.}\) \(x\in [a] \Rightarrow a r x \text{.}\) Also, there exists an element, \(y\text{,}\) of \(A\) that is in the intersection of \([a]\) and \([b]\) by our assumption. Therefore,
\begin{equation*} \begin{split} a r y \land b r y &\Rightarrow a r y \land y r b \quad r\textrm{ is symmetric}\\ &\Rightarrow a r b \quad \textrm{ transitivity of }r \\ \end{split} \end{equation*}
Next,
\begin{equation*} \begin{split} a r x \land a r b &\Rightarrow x r a \land a r b\\ &\Rightarrow x r b\\ &\Rightarrow b r x\\ & \Rightarrow x \in [b]\\ \end{split} \end{equation*}
Similarly, \([b]\subseteq [a]\text{.}\) \(\square\)

6.3.4.9.

Answer.
  1. Equivalence Relation, \([0]=\{0\},[1]=\{1\},[2]=\{2,3\} =[3],[4]=\{4,5\}=[5]\text{,}\) and \([6]=\{6,7\}=[7]\)
  2. Not an Equivalence Relation.
  3. Equivalence Relation, \([0]=\{0,2,4,6\}=[2]=[4]=[6]\) and \([1]=\{1,3,5,7\}=[3]=[5]=[7]\)

6.3.4.11.

Answer.
  1. The proof follows from the biconditional equivalence in Table 3.4.4.
  2. Apply the chain rule.
  3. See Figure 6.3.21.
described in detail following the image
Solution to number 11 of Section 6.3
Figure 6.3.21.

6.4 Matrices of Relations
6.4.3 Exercises

6.4.3.1.

Answer.
  1. \(\begin{array}{cc} & \begin{array}{ccc} 4 & 5 & 6 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \\ \end{array}\) and \(\begin{array}{cc} & \begin{array}{ccc} 6 & 7 & 8 \\ \end{array} \\ \begin{array}{c} 4 \\ 5 \\ 6 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\)
  2. \(\displaystyle r_1r_2 =\{(3,6),(4,7)\}\)
  3. \(\displaystyle \begin{array}{cc} & \begin{array}{ccc} 6 & 7 & 8 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\)

6.4.3.3.

Answer.
Table 6.4.8.
R : \(x r y\) if and only if \(\lvert x -y \rvert = 1\)
S : \(x s y\) if and only if \(x\) is less than \(y\text{.}\)

6.4.3.5.

Hint.
Consider the possible matrices.
Answer.
The graph of a relation on three elements has nine entries. The three entries in the diagonal must be 1 in order for the relation to be reflexive. In addition, to make the relation symmetric, the off-diaginal entries can be paired up so that they are equal. For example if the entry in row 1 column 2 is equal to 1, the entry in row 2 column 1 must also be 1. This means that three entries, the ones above the diagonal determine the whole matrix, so there are \(2^3=8\) different reflexive, symmetric relations on a three element set.

6.4.3.7.

Answer.
  1. \(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\) and \(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} \right) \\ \end{array}\)
  2. \(P Q= \begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\) \(P^2 =\text{ } \begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} \right) \\ \end{array}\)\(=Q^2\)

6.4.3.9.

Answer.
  1. Reflexive: \(R_{ij}=R_{ij}\) for all \(i,j\text{,}\) therefore \(R_{ij}\leq R_{ij}\)
    Antisymmetric: Assume \(R_{ij}\leq S_{ij}\) and \(S_{ij}\leq R_{ij}\) for all \(1\leq i,j\leq n\text{.}\) Therefore, \(R_{ij} = S_{ij}\) for all \(1\leq i,j\leq n\) and so \(R=S\)
    Transitive: Assume \(R, S,\) and \(T\) are matrices where \(R_{ij}\leq S_{ij}\) and \(S_{ij}\leq T_{ij}\text{,}\) for all \(1\leq i,j\leq n\text{.}\) Then \(R_{ij}\leq T_{ij}\) for all \(1\leq i,j\leq n\text{,}\) and so \(R\leq T\text{.}\)
  2. \begin{equation*} \begin{split} \left(R^2\right)_{ij}&=R_{i1}R_{1j}+R_{i2}R_{2j}+\cdots +R_{in}R_{nj}\\ &\leq S_{i1}S_{1j}+S_{i2}S_{2j}+\cdots +S_{in}S_{nj}\\ &=\left(S^2\right)_{ij} \Rightarrow R^2\leq S^2 \end{split}\text{.} \end{equation*}
    To verify that the converse is not true we need only one example. For \(n=2\text{,}\) let \(R_{12}=1\) and all other entries equal \(0\text{,}\) and let \(S\) be the zero matrix. Since \(R^2\) and \(S^2\) are both the zero matrix, \(R^2\leq S^2\text{,}\) but since \(R_{12}>S_{12}, R\leq S\) is false.
  3. The matrices are defined on the same set \(A=\left\{a_1,a_2,\ldots ,a_n\right\}\text{.}\) Let \(c\left(a_i\right), i=1,2,\ldots ,n\) be the equivalence classes defined by \(R\) and let \(d\left(a_i\right)\) be those defined by \(S\text{.}\) Claim: \(c\left(a_i\right)\subseteq d\left(a_i\right)\text{.}\)
    \begin{equation*} \begin{split} a_j\in c\left(a_i\right)&\Rightarrow a_i r a_j\\ &\Rightarrow R_{ij}=1 \Rightarrow S_{ij}=1\\ &\Rightarrow a_i s a_j\\ & \Rightarrow a_j \in d\left(a_i\right)\\ \end{split} \end{equation*}

6.5 Closure Operations on Relations
6.5.3 Exercises

6.5.3.3.

Answer.
  1. See graphs below.
  2. For example, \(0 s^+ 4\) and using \(S\) one can go from 0 to 4 using a path of length 3.
digraph of S
Figure 6.5.10. Digraph of \(\mathcal{S}\)
Figure 6.5.11. Digraph of \(\mathcal{S}^2\)
Figure 6.5.12. Digraph of \(\mathcal{S}^3\)
Figure 6.5.13. Digraph of \(\mathcal{S}^+\)

6.5.3.5.

Answer.
Definition: Reflexive Closure. Let \(r\) be a relation on \(A\text{.}\) The reflexive closure of \(r\) is the smallest reflexive relation that contains \(r\text{.}\)
Theorem: The reflexive closure of \(r\) is the union of \(r\) with \(\{(x, x) : x\in A\}\)

6.5.3.7.

Answer.
  1. By the definition of transitive closure, \(r^+\) is the smallest relation which contains \(r\text{;}\) therefore, it is transitive. The transitive closure of \(r^+\text{,}\) \(\left(r^+\right)^+\) , is the smallest transitive relation that contains \(r^+\text{.}\) Since \(r^+\) is transitive, \(\left(r^+\right)^+=r^+\text{.}\)
  2. The transitive closure of a symmetric relation is symmetric, but it may not be reflexive. If one element is not related to any elements, then the transitive closure will not relate that element to others.

7 Functions
7.1 Definition and Notation
7.1.5 Exercises

7.1.5.1.

Answer.
  1. Yes
  2. Yes
  3. No
  4. No
  5. Yes

7.1.5.3.

Answer.
  1. Range of \(f=f(A)=\{a,b,c,d\}=B\)
  2. Range of \(g=g(A)=\{a,b,d\}\)
  3. \(h\) is not a function.
  4. \(k\) is not a function.
  5. Range of \(L=L(A)=\{1\}\)

7.1.5.5.

Answer.
For each of the \(\lvert A \rvert \) elements of \(A\text{,}\) there are \(\lvert B \rvert\) possible images, so there are \(\lvert B \rvert\cdot \lvert B \rvert\cdot \ldots \cdot \lvert B \rvert=\left\lvert B \rvert^{\lvert A \rvert}\right.\) functions from \(A\) into \(B\text{.}\)

7.2 Properties of Functions
7.2.3 Exercises

7.2.3.1.

Answer.
The only one-to-one function and the only onto function is \(f\text{.}\)

7.2.3.3.

Answer.
  1. \(f_1\) is onto but not one-to-one: \(f_1(0)=f_1(1)\text{.}\)
  2. \(f_2\) is one-to-one and onto.
  3. \(f_3\) is one-to-one but not onto.
  4. \(f_4\) is onto but not one-to-one.
  5. \(f_5\) is one-to-one but not onto.
  6. \(f_6\) is one-to-one but not onto.

7.2.3.5.

Answer.
Let \(X=\{\textrm{socks selected}\}\) and \(Y=\{\textrm{pairs of socks}\}\) and define \(f:X \to Y\) where \(f(x) =\)the pair of socks that \(x\) belongs to . By the Pigeonhole principle, there exist two socks that were selected from the same pair.

7.2.3.7.

Answer.
  1. \(f(n)=n\text{,}\) for example
  2. \(f(n)=1\text{,}\) for example
  3. None exist.
  4. None exist.

7.2.3.9.

Answer.
  1. Use \(s:\mathbb{N}\to \mathbb{P}\) defined by \(s(x)=x+1\text{.}\)
  2. Use the function\(f:\mathbb{N}\to \mathbb{Z}\) defined by \(f(\text{x0}=x/2\) if \(x\) is even and \(f(x)=-(x+1)/2\) if \(x\) is odd.
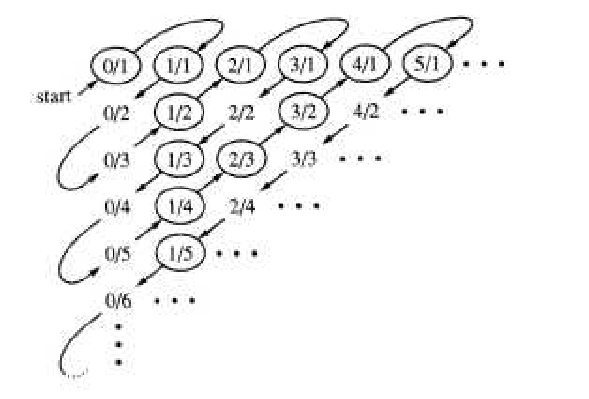
  3. The proof is due to Georg Cantor (1845-1918), and involves listing the rationals through a definite procedure so that none are omitted and duplications are avoided. In the first row list all nonnegative rationals with denominator 1, in the second all nonnegative rationals with denominator 2, etc. In this listing, of course, there are duplications, for example, \(0/1=0/2=0\text{,}\) \(1/1=3/3=1\text{,}\) \(6/4=9/6=3/2\text{,}\) etc. To obtain a list without duplications follow the arrows in Figure 7.2.15, listing only the circled numbers.
    We obtain: \(0,1,1/2,2,3,1/3,1/4,2/3,3/2,4/1,\ldots\) Each nonnegative rational appears in this list exactly once. We now must insert in this list the negative rationals, and follow the same scheme to obtain:
    \begin{equation*} 0,1,-1,1/2,-1/2,2,-2,3,-3,1/3,-1/3, \ldots \end{equation*}
    which can be paired off with the elements of \(\mathbb{N}\text{.}\)
Figure 7.2.15. Enumeration of the rational numbers.

7.2.3.11.

Answer.
Let \(f\) be any function from \(A\) into \(B\text{.}\) By the Pigeonhole principle with \(n=1\text{,}\) there exists an element of \(B\) that is the image of at least two elements of \(A\text{.}\) Therefore, \(f\) is not an injection.

7.2.3.13.

Answer.
The proof is indirect and follows a technique called the Cantor diagonal process. Assume to the contrary that the set is countable, then the elements can be listed: \(n_1,n_2,n_3,\ldots\) where each \(n_i\) is an infinite sequence of 0s and 1s. Consider the array:
\begin{equation*} \begin{array}{c} n_1=n_{11}n_{12}n_{13}\cdots\\ n_2=n_{21}n_{22}n_{23}\cdots\\ n_3=n_{31}n_{32}n_{33}\cdots\\ \quad \vdots\\ \end{array} \end{equation*}
We assume that this array contains all infinite sequences of 0s and 1s. Consider the sequence \(s\) defined by \(s_i=\begin{cases} 0 & \textrm{ if } n_{\textrm{ii}}=1 \\ 1 & \textrm{ if } n_{\textrm{ii}}=0 \end{cases}\)
Notice that \(s\) differs from each \(n_i\) in the \(i\)th position and so cannot be in the list. This is a contradiction, which completes our proof.

7.3 Function Composition
7.3.4 Exercises

7.3.4.1.

Answer.
  1. \(g\circ f:A\to C\) is defined by \((g\circ f)(k)=\begin{cases} + & \textrm{ if } k=1 \textrm{ or } k=5 \\ - & \textrm{ otherwise} \end{cases}\)
  2. No, since the domain of \(f\) is not equal to the codomain of \(g\text{.}\)
  3. No, since \(f\) is not surjective.
  4. No, since \(g\) is not injective.

7.3.4.3.

Answer.
  1. The permutations of \(A\) are \(i,r_1,r_2,f_1,f_2,\) and \(f_3\text{,}\) defined in Table 15.3.1.
  2. \begin{equation*} \begin{array}{ccc} g & g^{-1} & g^2 \\ i & i & i \\ r_1 & r_2 & r_2 \\ r_2 & r_1 & r_1 \\ f_1 & f_1 & i \\ f_2 & f_2 & i \\ f_3 & f_3 & i \\ \end{array} \end{equation*}
  3. If \(f\) and \(g\) are permutations of \(A\text{,}\) then they are both injections and their composition, \(f\circ g\text{,}\) is a injection, by Theorem 7.3.6. By Theorem 7.3.7, \(f\circ g\) is also a surjection; therefore, \(f\circ g\) is a bijection on \(A\text{,}\) a permutation.
  4. Proof by induction: Basis: \((n=1)\text{.}\) The number of permutations of \(A\) is one, the identity function, and 1! \(=1\text{.}\)
    Induction: Assume that the number of permutations on a set with \(n\) elements, \(n\geq 1\text{,}\) is \(n\text{!.}\) Furthermore, assume that \(|A|=\)\(\text{ }n+1\) and that \(A\) contains an element called \(\sigma\text{.}\) Let \(A'=A-\{\sigma\}\text{.}\) We can reduce the definition of a permutation, \(f\text{,}\) on \(A\) to two steps. First, we select any one of the \(n\text{!}\) permutations on \(A'\text{.}\) (Note the use of the induction hypothesis.) Call it \(g\text{.}\) This permutation almost completely defines a permutation on \(A\) that we will call \(f\text{.}\) For all \(a\) in \(A'\text{,}\) we start by defining \(f(a)\) to be \(g(a)\text{.}\) We may be making some adjustments, but define it that way for now. Next, we select the image of \(\sigma\text{,}\) which can be done \(n+1\) different ways, allowing for any value in \(A\text{.}\) To keep our function bijective, we must adjust \(f\) as follows: If we select \(f(\sigma)=y \neq \sigma\text{,}\) then we must find the element, \(z\text{,}\) of \(A\) such that \(g(z)=y\text{,}\) and redefine the image of \(z\) to \(f(z)=\sigma\text{.}\) If we had selected \(f(\sigma)=\sigma\text{,}\) then there is no adjustment needed. By the rule of products, the number of ways that we can define \(f\) is \(n!(n+1)=(n+1)!\) \(\square\)

7.3.4.5.

Answer.
  1. \(f_1\) has an inverse. \(f_1^{-1}= f_1^3\text{.}\)
  2. \(f_2\) has an inverse. \(f_2^{-1}= f_2\text{.}\)
  3. \(f_3\) does not have an inverse. One way to verify this is to note that \(f_3\) is not one-to-one because \(f_3(0000) = 0000 = f_3(1111)\text{.}\)
  4. \(f_4\) has an inverse. \(f_4^{-1}=f_4^3.\)

7.3.4.7.

Answer.
  1. \(\displaystyle f\circ g(n)=n+3\)
  2. \(\displaystyle f^3(n)=n+15\)
  3. \(\displaystyle f\circ h(n)=n^2+5\)

7.3.4.9.

Hint.
You have seen a similar proof in matrix algebra.

7.3.4.11.

Answer.
If \(f:A\to B\) and \(f\) has an inverse, then that inverse is unique.
Proof: Suppose that \(g\) and \(h\) are both inverses of \(f\text{,}\) both having domain \(B\) and codomain \(A\text{.}\)
\begin{equation*} \begin{split}g &= g\circ i_B \\ & =g\circ (f\circ h)\\ & =(g\circ f)\circ h\\ & =i_A\circ h\\ & =h\quad \Rightarrow g=h \quad \blacksquare \end{split} \end{equation*}

7.3.4.12.

Hint.
See Exercise 3 of Section 5.4.

7.3.4.13.

Answer.
Let \(x,x'\) be elements of \(A\) such that \(g\circ f(x)=g\circ f(x')\text{;}\) that is, \(g(f(x))=g(f(x'))\text{.}\) Since \(g\) is injective, \(f(x)=f(x')\) and since \(f\) is injective, \(x=x'\text{.}\) \(\square\)
Let \(x\) be an element of \(C\text{.}\) We must show that there exists an element of \(A\) whose image under \(g\circ f\) is \(x\text{.}\) Since \(g\) is surjective, there exists an element of \(B\text{,}\) \(y\text{,}\) such that \(g(y)=x\text{.}\) Also, since \(f\) is a surjection, there exists an element of \(A\text{,}\) \(z\text{,}\) such that \(f(z)=y\text{,}\) \(g\circ f(z)=g(f(z))=g(y)=x\text{.}\)\(\square\)

7.3.4.15.

Answer.
Basis: \((n=2)\text{:}\) \(\left(f_1\circ f_2\right){}^{-1}=f_2{}^{-1}\circ f_1{}^{-2}\) by Exercise 7.3.4.12.
Induction: Assume \(n\geq 2\) and
\begin{equation*} \left(f_1\circ f_2\circ \cdots \circ f_n\right){}^{-1}= f_n{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1} \end{equation*}
and consider \(\left(f_1\circ f_2\circ \cdots \circ f_{n+1}\right)^{-1}\text{.}\)
\begin{equation*} \begin{split} \left(f_1\circ f_2\circ \cdots \circ f_{n+1}\right){}^{-1} &=\left(\left(f_1\circ f_2\circ \cdots \circ f_n\right)\circ f_{n+1}\right){}^{-1}\\ & =f_{n+1}{}^{-1}\circ \left(f_1\circ f_2\circ \cdots \circ f_n\right){}^{-1}\\ & \quad \quad \quad \textrm{ by the basis}\\ &=f_{n+1}{}^{-1}\circ \left(f_n{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1}\right)\\ & \quad \quad \quad \textrm{ by the induction hypothesis}\\ &=f_{n+1}{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1} \quad. \square \end{split} \end{equation*}

8 Recursion and Recurrence Relations
8.1 The Many Faces of Recursion
8.1.8 Exercises

8.1.8.1.

Answer.
\begin{equation*} \begin{split} \binom{7}{2} &=\binom{6}{2} +\binom{6}{1} \\ &=\binom{5}{2} +\binom{5}{1} +\binom{5}{1} +\binom{5}{0} \\ &=\binom{5}{2} +2 \binom{5}{1} +1\\ &=\binom{4}{2} +\binom{4}{1} +2(\binom{4}{1} +\binom{4}{0} )+1\\ &=\binom{4}{2} +3 \binom{4}{1} + 3\\ &=\binom{3}{2} +\binom{3}{1} +3(\binom{3}{1} +\binom{3}{0} )+3\\ &=\binom{3}{2} +4 \binom{3}{1} + 6\\ &=\binom{2}{2} +\binom{2}{1} + 4(\binom{2}{1} +\binom{2}{0} ) + 6\\ &=5 \binom{2}{1} + 11\\ &=5(\binom{1}{1} +\binom{1}{0} ) + 11\\ &=21 \end{split} \end{equation*}

8.1.8.3.

Answer.
  1. \(p(x)\) in telescoping form: \(((((x+3)x-15)x+0)x+1)x-10\)
  2. \(\displaystyle p(3)=((((3+3)3-15)3-0)3+1)3-10=74\)

8.1.8.5.

Answer.
The basis is not reached in a finite number of steps if you try to compute \(f(x)\) for a nonzero value of \(x\text{.}\)

8.2 Sequences
8.2.3 Exercises

8.2.3.1.

Answer.
Basis: \(B(0)=3\cdot 0+2=2\text{,}\) as defined.
Induction: Assume: \(B(k)=3k+2\) for some \(k\geq 0\text{.}\)
\begin{equation*} \begin{split} B(k+1) &=B(k)+3\\ &=(3k+2)+3\quad \textrm{ by the induction hypothesis} \\ &=(3k+3)+2\\ &=3(k+1)+2\quad \textrm{as desired} \end{split} \end{equation*}

8.2.3.3.

Answer.
Imagine drawing line \(k\) in one of the infinite regions that it passes through. That infinite region is divided into two infinite regions by line \(k\text{.}\) As line \(k\) is drawn through every one of the \(k-1\) previous lines, you enter another region that line \(k\) divides. Therefore \(k\) regions are divided and the number of regions is increased by \(k\text{.}\) From this observation we get \(P(5)=16\text{.}\)

8.2.3.5.

Answer.
For \(n\) greater than zero, \(M(n)=M(n-1)+1\text{,}\) and \(M(0)=0\text{.}\)

8.3 Recurrence Relations
8.3.5 Exercises

8.3.5.1.

Answer.
\(S(k)=2+9^k\)

8.3.5.3.

Answer.
\(S(k)=6(1/4)^k\)

8.3.5.5.

Answer.
\(S(k)=k^2-10k+25\)

8.3.5.7.

Answer.
\(S(k)=(3+k)5^k\)

8.3.5.9.

Answer.
\(S(k)=(12+3k)+\left(k^2+7k-22\right)2^{k-1}\)

8.3.5.11.

Answer.
\(S(k)=4(-3)^k+2^k-5^{k+1}\)

8.3.5.13.

Answer.
  1. The characteristic equation is \(a^2-a-1=0\text{,}\) which has solutions \(\alpha =\left.\left(1+\sqrt{5}\right)\right/2\) and \(\beta =\left.\left(1-\sqrt{5}\right)\right/2\text{,}\) It is useful to point out that \(\alpha +\beta =1\) and \(\alpha -\beta =\sqrt{5}\text{.}\) The general solution is \(F(k)=b_1\alpha ^k+b_2\beta ^k\text{.}\) Using the initial conditions, we obtain the system: \(b_1+b_2=1\) and \(b_1\alpha +b_2\beta =1\text{.}\) The solution to this system is \(b_1=\alpha /(\alpha -\beta )=\left.\left(5+\sqrt{5}\right)\right/2\sqrt{5}\) and \(b_2=\beta /(\alpha -\beta )=\left.\left(5-\sqrt{5}\right)\right/2\sqrt{5}\)
    Therefore the final solution is
    \begin{equation*} \begin{split} F(n) & = \frac{\alpha^{n+1}-\beta^{n+1}}{\alpha-\beta} \\ & = \frac{\left(\left.\left(1+\sqrt{5}\right)\right/2\right)^{n+1} -\left(\left.\left(1-\sqrt{5}\right)\right/2\right)^{n+1}}{\sqrt{5}}\\ \end{split} \end{equation*}
  2. \(\displaystyle C_r=F(r+1)\)

8.3.5.15.

Answer.
  1. For each two-block partition of \(\{1,2,\dots, n-1\}\text{,}\) there are two partitions we can create when we add \(n\text{,}\) but there is one additional two-block partition to count for which one block is \(\{n\}\text{.}\) Therefore, \(D(n)=2D(n-1)+1 \textrm{ for } n \geq 2 \textrm{ and } D(1)=0.\)
  2. \(\displaystyle D(n)=2^{n-1}-1\)

8.4 Some Common Recurrence Relations
8.4.5 Exercises

8.4.5.1.

Answer.
  1. \(S(n)=1/n\text{!}\)
  2. \(U(k)=1/k\text{,}\) an improvement.
  3. \(T(k)=(-3)^kk\text{!,}\) no improvement.

8.4.5.3.

Answer.
  1. \(\displaystyle T(n)=3\left(\left\lfloor \log_2n\right\rfloor +1\right)\)
  2. \(\displaystyle T(n)=2\)
  3. \(\displaystyle V(n)=\left\lfloor \log_8n\right\rfloor +1\)

8.4.5.4.

Hint.
Prove by induction on \(r\text{.}\)

8.4.5.5.

Answer.
The indicated substitution yields \(S(n)=S(n+1)\text{.}\) Since \(S(0)=T(1)/T(0)=6\text{,}\) \(S(n)=6\) for all \(n\text{.}\) Therefore \(T(n+1)=6T(n)\Rightarrow T(n)=6^n\text{.}\)

8.4.5.7.

Answer.
  1. A good approximation to the solution of this recurrence relation is based on the following observation: \(n\) is a power of a power of two; that is, \(n\) is \(2^m\text{,}\) where \(m=2^k\) , then \(Q(n)=1+Q\left(2^{m/2}\right)\text{.}\) By applying this recurrence relation \(k\) times we obtain \(Q(n)=k\text{.}\) Going back to the original form of \(n\text{,}\) \(\log _2n=2^k\) or \(\log _2\left(\log _2n\right)=k\text{.}\) We would expect that in general, \(Q(n)\) is \(\left\lfloor \log _2\left(\log _2n\right)\right\rfloor\text{.}\) We do not see any elementary method for arriving at an exact solution.
  2. Suppose that \(n\) is a positive integer with \(2^{k-1} \leq n < 2^k\text{.}\) Then \(n\) can be written in binary form, \(\left(a_{k-1}a_{k-2}\cdots a_2a_1a_0\right)_{\textrm{two}}\) with \(a_{k-1}=1\) and \(R(n)\) is equal to the sum \(\underset{i=0}{\overset{k-1}{\Sigma }}\) \(\left(a_{k-1}a_{k-2}\cdots a_i\right)_{\textrm{two}}\text{.}\) If \(2^{k-1}\leq n < 2^k\text{,}\) then we can estimate this sum to be between \(2n-1\) and \(2n+1\text{.}\) Therefore, \(R(n)\approx 2n\text{.}\)

8.5 Generating Functions
8.5.7 Exercises

8.5.7.1.

Answer.
  1. \(\displaystyle 1,0,0,0,0,\ldots\)
  2. \(\displaystyle 5(1/2)^k\)
  3. \(\displaystyle 1,1,0,0,0,\ldots\)
  4. \(\displaystyle 3(-2)^k+3\cdot 3^k\)

8.5.7.3.

Answer.
  1. \(\displaystyle 1/(1-9z)\)
  2. \(\displaystyle (2-10z)\left/\left(1-6z+5z^2\right)\right.\)
  3. \(\displaystyle 1\left/\left(1-z-z^2\right)\right.\)

8.5.7.5.

Answer.
  1. \(\displaystyle 3/(1-2z)+2/(1+2z), 3\cdot 2^k+2(-2)^k\)
  2. \(\displaystyle 10/(1-z)+12/(2-z), 10+6(1/2)^k\)
  3. \(\displaystyle -1/(1-5z)+7/(1-6z), 7\cdot 6^k-5^k\)

8.5.7.7.

Answer.
  1. \(\displaystyle 11k\)
  2. \(\displaystyle (5/3)k(k+1)(k+2)\)
  3. \(\underset{j=0}{\overset{k}{\Sigma }}(j)(10(k-j))=10k\underset{j=0}{\overset{k}{\Sigma }}j-10\underset{j=0}{\overset{k}{\Sigma }}j^2\) \(=(5/3)(k-1)k(k+1)\)
  4. \(\displaystyle k(k+1)(k+3)/6\)

8.5.7.9.

Answer.
Coefficients of \(z^0\) through \(z^5\) in \((1+5z)(2+4z)(3+3z)(4+2z)(5+z)\)
\(\begin{array}{cc} k & \textrm{ Number of ways of getting a score of } k \\ 0 & 120 \\ 1 & 1044 \\ 2 & 2724 \\ 3 & 2724 \\ 4 & 1044 \\ 5 & 120 \\ \end{array}\)

9 Graph Theory
9.1 Graphs - General Introduction
9.1.5 Exercises

9.1.5.1.

Answer.
In Figure 9.1.8, computer \(b\) can communicate with all other computers. In Figure 9.1.9, there are direct roads to and from city \(b\) to all other cities.

9.1.5.3.

Answer.
described in detail following the image
Solution to exercise 3 of Section 9.1
Figure 9.1.37. Solution to exercise 3 of Section 9.1

9.1.5.5.

Answer.
The maximum number of edges would be \(\binom{8}{2} = \frac{(7)(8)}{2}=28\text{.}\)

9.1.5.7.

Answer.
  1. \(\displaystyle \binom{n}{2}=\frac{(n-1)n}{2}\)
  2. \(n-1\text{,}\) each vertex except the champion vertex has an indegree of 1 and the champion vertex has an indegree of zero.

9.1.5.9.

Answer.
  1. Not graphic - if the degree of a graph with seven vertices is 6, it is connected to all other vertices and so there cannot be a vertex with degree zero.
  2. Graphic. One graph with this degree sequence is a cycle of length 6.
  3. Not Graphic. The number of vertices with odd degree is odd, which is impossible.
  4. Graphic. A "wheel graph" with one vertex connected to all other and the others connected to one another in a cycle has this degree sequence.
  5. Graphic. Pairs of vertices connected only to one another.
  6. Not Graphic. With two vertices having maximal degree, 5, every vertex would need to have a degree of 2 or more, so the 1 in this sequence makes it non-graphic.

9.2 Data Structures for Graphs
9.2.3 Exercises

9.2.3.1.

Answer.
  1. A rough estimate of the number of vertices in the “world airline graph” would be the number of cities with population greater than or equal to 100,000. This is estimated to be around 4,100. There are many smaller cities that have airports, but some of the metropolitan areas with clusters of large cities are served by only a few airports. 4,000-5,000 is probably a good guess. As for edges, that’s a bit more difficult to estimate. It’s certainly not a complete graph. Looking at some medium sized airports such as Manchester, NH, the average number of cities that you can go to directly is in the 50-100 range. So a very rough estimate would be \(\frac{75 \cdot 4500}{2}=168,750\text{.}\) This is far less than \(4,500^2\text{,}\) so an edge list or dictionary of some kind would be more efficient.
  2. The number of ASCII characters is 128. Each character would be connected to \(\binom{8}{2}=28\) others and so there are \(\frac{128 \cdot 28}{2}=3,584\) edges. Comparing this to the \(128^2=16,384\text{,}\) an array is probably the best choice.
  3. The Oxford English Dictionary as approximately a half-million words, although many are obsolete. The number of edges is probably of the same order of magnitude as the number of words, so an edge list or dictionary is probably the best choice.

9.2.3.3.

Answer.
Each graph is isomorphic to itself. In addition, \(G_2 \text{ and } G_4\) are isomorphic; and \(G_3, G_5, \text{ and } G_6\) are isomorphic to one another.

9.3 Connectivity
9.3.6 Exercises

9.3.6.1.

Answer.
\begin{equation*} \begin{array}{ccccccc} k & 1 & 2 & 3 & 4 & 5 & 6 \\ V[k].\text{found} & T & T & T & F & F & T \\ V[k].\text{from} & 2 & 5 & 6 & * & * & 5 \\ \text{Depth} \text{Set} & 2 & 1 & 2 & * & * & 1 \\ \end{array} \end{equation*}
\(\text{(*} = \text{undefined})\)

9.3.6.3.

Answer.
If the number of vertices is \(n\text{,}\) there can be \(\frac{(n-1)(n-2)}{2}\) vertices with one vertex not connected to any of the others. One more edge and connectivity is assured.

9.3.6.5.

Answer.
  1. The eccentricity of each vertex is 2; and the diameter and radius are both 2 as well. All vertices are part of the center.
  2. The corners (1,3,10 and 10) have eccentricities 5. The two central vertices, 5 and 8, which are in the center of the graph have eccentricity 3. All other vertices have eccentricity 4. The diameter is 5. The radius is 3.
  3. Vertices 1, 2 and 5 have eccentricity 2 and make up the center of this graph. Verticies 7 and 8 have eccentricity 4, and all other vertices have eccentricity 3. The diameter is 4. The radius is 2.
  4. The eccentricity of each vertex is 4; and the diameter and radius are both 4 as well. All vertices are part of the center.

9.3.6.7.

Answer.
Basis: \((k=1)\) Is the relation \(r^1\text{,}\) defined by \(v r^1 w\) if there is a path of length 1 from \(v \text{ to } w\text{?}\) Yes, since \(v r w\) if and only if an edge, which is a path of length \(1\text{,}\) connects \(v\) to \(w\text{.}\)
Induction: Assume that \(v r^k w\) if and only if there is a path of length \(k\) from \(v\) to \(w\text{.}\) We must show that \(v r^{k+1} w\) if and only if there is a path of length \(k+1\) from \(v\) to \(w\text{.}\)
\begin{equation*} v r^{k+1} w \Rightarrow v r^k y \textrm{ and } y r w\textrm{ for some vertex } y \end{equation*}
By the induction hypothesis, there is a path of length \(k\) from \(v \textrm{ to } y\text{.}\) And by the basis, there is a path of length one from \(y\) to \(w\text{.}\) If we combine these two paths, we obtain a path of length \(k+1\) from \(v\) to \(w\text{.}\) Of course, if we start with a path of length \(k+1\) from \(v\) to \(w\text{,}\) we have a path of length \(k\) from \(v\) to some vertex \(y\) and a path of length 1 from \(y\) to \(w\text{.}\) Therefore, \(v r^k y \textrm{ and } y r w \Rightarrow v r^{k+1} w\text{.}\)

9.4 Traversals: Eulerian and Hamiltonian Graphs
9.4.3 Exercises

9.4.3.1.

Answer.
Using a recent road map, it appears that an Eulerian circuit exists in New York City, not including the small islands that belong to the city. Lowell, Massachusetts, is located at the confluence of the Merrimack and Concord rivers and has several canals flowing through it. No Eulerian path exists for Lowell.

9.4.3.3.

Answer.
Gray Code for the 4-cube:
\begin{equation*} G_4=\left( \begin{array}{c} 0000 \\ 0001 \\ 0011 \\ 0010 \\ 0110 \\ 0111 \\ 0101 \\ 0100 \\ 1100 \\ 1101 \\ 1111 \\ 1110 \\ 1010 \\ 1011 \\ 1001 \\ 1000 \\ \end{array} \right) \end{equation*}

9.4.3.5.

Answer.
Any bridge between two land masses will be sufficient. To get an Eulerian circuit, you must add a second bridge that connects the two land masses that were not connected by the first bridge.

9.4.3.7.

Answer.
Let \(G=(V,E)\) be a directed graph. \(G\) has an Eulerian circuit if and only if \(G\) is connected and \(indeg(v)= outdeg(v)\) for all \(v \in V\text{.}\) There exists an Eulerian path from \(v_1 \textrm{ to } v_2\) if and only if \(G\) is connected, \(indeg(v_1)=outdeg(v_1)-1\text{,}\) \(indeg(v_2)= outdeg(v_2)+1\text{,}\) and for all other vertices in \(V\) the indegree and outdegree are equal.

9.4.3.8.

Hint.
You could prove this by induction on the number of edges, but an easier way would be to consider the degree sequence and use something you know about the sum of the entries.

9.4.3.9.

Answer.
A round-robin tournament graph is rarely Eulerian. It will be Eulerian if it has an odd number of vertices and each vertex (team) wins exactly as many times as it loses. Every round-robin tournament graph has a Hamiltonian path. This can be proven by induction on the number of vertices.

9.4.3.11.

Solution.
No, such a line does not exist. The dominoes with two different numbers correspond with edges in a \(K_6\text{.}\) See corresponding dominos and edges in Figure 9.4.25. Dominos with two equal numbers could be held back and inserted into the line created with the other dominoes if such a line exists. For example, if \((2,5),(5,4)\) were part of the line, \((5,5)\) could be inserted between those two dominoes. The line we want exists if and only if there exists an Eulerian path in a \(K_6\text{.}\) Since all six vertices of a \(K_6\) have odd degree no such path exists.
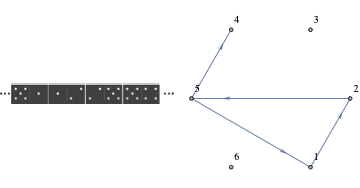
described in detail following the image
Four dominos lay end-to-end with numbers on abutting ends matching. They correspond with four connecting edges in a \(K_6\text{.}\)
Figure 9.4.25. Correspondence between a line of dominos and a path in a \(K_6\)

9.5 Graph Optimization
9.5.5 Exercises

9.5.5.1.

Answer.
The circuit would be Boston, Providence, Hartford, Concord, Montpelier, Augusta, Boston. It does matter where you start. If you start in Concord, for example, your mileage will be higher.

9.5.5.3.

Answer.
  1. Optimal cost \(=2\sqrt{2}\text{.}\) Phase 1 cost \(=2.4\sqrt{2}\text{.}\) Phase 2 cost \(=2.6\sqrt{2}\text{.}\)
  2. Optimal cost \(=2.60.\) Phase 1 cost \(=3.00\text{.}\) Phase 2 cost \(2\sqrt{2}\text{.}\)
  3. \(A=(0.0, 0.5), B=(0.5, 0.0), C=(0.5, 1.0), D=(1.0, 0.5)\)
    There are 4 points; so we will divide the unit square into two strips.
    • Optimal Path: \((B,A,C,D)\quad \quad \text{Distance } =2\sqrt{2}\)
    • Phase I Path: \((B,A,C,D)\quad \quad \text{Distance }=2\sqrt{2}\)
    • Phase II Path: \((A,C,B,D) \quad \quad\textrm{Distance }=2+\sqrt{2}\)
  4. \(A=(0,0), B=(0.2,0.6), C=(0.4,0.1), D=(0.6,0.8), E=(0.7,0.5)\)
    There are 5 points; so we will divide the unit square into three strips.
    • Optimal Path: \((A,B,D,E,C)\quad \quad \text{Distance }=2.31\)
    • Phase I Path: \((A,C,B,C,E)\quad \quad \text{Distance }= 2.57\)
    • Phase II Path: \((A,B,D,E,C) \quad \quad\textrm{Distance }=2.31\)

9.5.5.5.

Answer.
  1. \(f(c,d)=2\text{,}\) \(f(b,d)=2\text{,}\) \(f(d,k)=5\text{,}\) \(f(a,g)=1\text{,}\) and \(f(g,k)=1\text{.}\)
  2. There are three possible flow-augmenting paths. \(s,b,d,k\) with flow increase of 1. \(s,a,d,k\) with flow increase of 1, and \(s,a,g,k\) with flow increase of 2.
  3. The new flow is never maximal, since another flow-augmenting path will always exist. For example, if \(s,b,d,k\) is used above, the new flow can be augmented by 2 units with \(s,a,g,k\text{.}\)

9.5.5.7.

Answer.
  1. Value of maximal flow \(=31\text{.}\)
  2. Value of maximal flow \(=14\text{.}\)
  3. Value of maximal flow \(=14\text{.}\) See Table 9.5.35 for one way to got this flow.
Table 9.5.35.
Step Flow-augmenting path Flow added
1 \(\text{Source},A,\text{Sink}\) 2
2 \(\text{Source}, C,B, \text{Sink}\) 3
3 \(\text{Source},E,D, \text{Sink}\) 4
4 \(\text{Source},A,B,\text{Sink}\) 1
5 \(\text{Source},C,D, \text{Sink}\) 2
6 \(\text{Source},A,B,C,D, \text{Sink}\) 2

9.5.5.9.

Hint.
Count the number of comparisons of distances that must be done.
Answer.
To locate the closest neighbor among the list of \(k\) other points on the unit square requires a time proportional to \(k\text{.}\) Therefore the time required for the closest-neighbor algorithm with \(n\) points is proportional to \((n-1)+(n-2)+\cdots +2+1\text{,}\) which is proportional to \(n^2\text{.}\) Since the strip algorithm takes a time proportional to \(n(\log n)\text{,}\) it is much faster for large values of \(n\text{.}\)

9.6 Planarity and Colorings
9.6.3 Exercises

9.6.3.1.

Answer.
A \(K_5\) has 10 edges. If a \(K_5\) is planar, the number of regions into which the plane is divided must be 7, by Euler’s formala (\(5+7-10=2\)). If we re-count the edges of the graph by counting the number edges bordering the regions we get a count of at least \(7 \times 3=21\text{.}\) But we’ve counted each edge twice this way and the count must be even. This implies that the number of edges is at least 11, which a contradiction.

9.6.3.3.

Answer.
  1. 4
  2. 3
  3. 3
  4. 3
  5. 2
  6. 4

9.6.3.5.

Answer.
The chromatic number is \(n\) since every vertex is connected to every other vertex.

9.6.3.7.

Answer.
Suppose that \(G'\) is not connected. Then \(G'\) is made up of 2 components that are planar graphs with less than \(k\) edges, \(G_1\) and \(G_2\text{.}\) For \(i=1,2\) let \(v_i,r_i, \text{and} e_i\) be the number of vertices, regions and edges in \(G_i\text{.}\) By the induction hypothesis, \(v_i+r_i-e_i=2\) for \(i=1,2\text{.}\)
One of the regions, the infinite one, is common to both graphs. Therefore, when we add edge \(e\) back to the graph, we have \(r=r_1+r_2-1\text{,}\) \(v=v_1+v_2\text{,}\) and \(e=e_1+e_2+1\text{.}\)
\begin{equation*} \begin{split} v+r-e &=\left(v_1+v_2\right)+\left(r_1+r_2-1\right)-\left(e_1+e_2+1\right)\\ &=\left(v_1+r_1-e_1\right)+\left(v_2+r_2-e_2\right)-2\\ &=2 + 2 -2\\ &=2 \end{split} \end{equation*}

9.6.3.9.

Answer.
Since \(\left| E\right| +\left| E^c \right|=\frac{n(n-1)}{2}\text{,}\) either \(E \text{ or } E^c\) has at least \(\frac{n(n-1)}{4}\) elements. Assume that it is \(E\) that is larger. Since \(\frac{n(n-1)}{4}\) is greater than \(3n-6\text{ }\text{for}\text{ }n\geqslant 11\text{,}\) \(G\) would be nonplanar. Of course, if \(E^c\) is larger, then \(G'\) would be nonplanar by the same reasoning. Can you find a graph with ten vertices such that it is planar and its complement is also planar?

9.6.3.11.

Answer.
Suppose that \((V,E)\) is bipartite (with colors red and blue), \(\left| E\right|\) is odd, and \(\left(v_1,v_2,\ldots ,v_{2n+1},v_1\right)\) is a Hamiltonian circuit. If \(v_1\) is red, then \(v_{2n+1}\) would also be red. But then \(\left\{v_{2n+1},v_1\right\}\) would not be in \(E\text{,}\) a contradiction.

9.6.3.13.

Answer.
Draw a graph with one vertex for each edge, If two edges in the original graph meet at the same vertex, then draw an edge connecting the corresponding vertices in the new graph.

10 Trees
10.1 What Is a Tree?
10.1.3 Exercises

10.1.3.1.

Answer.
The number of trees are: (a) 1, (b) 3, and (c) 16. The trees that connect \(V_c\) are:
Solution to exercise 10-1-1
Figure 10.1.12.

10.1.3.3.

Hint.
Use induction on \(\lvert E\rvert \text{.}\)

10.1.3.5.

Answer.
  1. Assume that \((V,E)\) is a tree with \(\left| V\right| \geq 2\text{,}\) and all but possibly one vertex in \(V\) has degree two or more.
    \begin{equation*} \begin{split} 2\lvert E \rvert =\sum_{v \in V}{\deg(v)} \geq 2 \lvert V \rvert -1 &\Rightarrow \lvert E\vert \geq \lvert V\rvert -\frac{1}{2}\\ &\Rightarrow \lvert E\rvert \geq \lvert V\rvert\\ & \Rightarrow (V,E) \textrm{ is not a tree.} \end{split} \end{equation*}
  2. The proof of this part is similar to part a in that we can infer \(2\lvert E\rvert \geq 2 \lvert V\rvert -1\text{,}\) using the fact that a non-chain tree has at least one vertex of degree three or more.

10.2 Spanning Trees
10.2.4 Exercises

10.2.4.1.

Answer.
It might not be most economical with respect to Objective 1. You should be able to find an example to illustrate this claim. The new system can always be made most economical with respect to Objective 2 if the old system were designed with that objective in mind.

10.2.4.3.

Answer.
In the figure below, \(\{1,2\}\) is not a minimal bridge between \(L=\{1,4\} \textrm{ and } R=\{2,3\}\text{,}\) but it is part of the minimal spanning tree for this graph.
Solution to exercise 10-2-3
Figure 10.2.16.

10.2.4.5.

Answer.
  1. Edges in one solution are: \(\{8,7\},\{8,9\},\{8,13\},\{7,6\},\{9,4\},\{13,12\},\{13,14\},\{6,11\},\{6,1\},\{1,2\},\{4,3\},\{4,5\},\{14,15\}, \textrm{ and } \{5,10\}\)
  2. Vertices 8 and 9 are centers of the graph. Starting from vertex 8, a minimum diameter spanning tree is \(\{\{8, 3\}, \{8, 7\}, \{8, 13\}, \{8, 14\}, \{8, 9\}, \{3, 2\}, \{3, 4\}, \{7, 6\}, \{13, 12\}, \{13, 19\}, \{14, 15\}, \{9, 16\}, \{9, 10\}, \{6, 1\}, \{12, 18\}, \{16, 20\}, \{16, 17\}, \{10, 11\}, \{20, 21\}, \{11, 5\}\}.\) The diameter of the tree is 7.

10.3 Rooted Trees
10.3.4 Exercises

10.3.4.1.

Answer.
Locate any simple path of length \(d\) and locate the vertex in position \(\lceil d/2\rceil\) on the path. The tree rooted at that vertex will have a depth of \(\lceil d/2\rceil\text{,}\) which is minimal.

10.3.4.3.

Answer.
Solution to exercise 10-3-3
Figure 10.3.16.

10.4 Binary Trees
10.4.6 Exercises

10.4.6.1.

Answer.
Solution to exercise 10-4-1-A
Figure 10.4.15.
Solution to exercise 10-4-1-B
Figure 10.4.16.

10.4.6.3.

Answer.
\begin{equation*} \begin{array}{cccc} & \text{Preorder} & \text{Inorder} & \text{Postorder} \\ (a) & \cdot a + b c & a\cdot b+c & a b c + \cdot \\ (b) & +\cdot a b c & a\cdot b+c & a b\cdot c+ \\ (c) & +\cdot a b\cdot a c & a\cdot b+a\cdot c & a b\cdot a c\cdot + \\ \end{array} \end{equation*}

10.4.6.5.

Answer.
There are \(2^6=64\) different possible answers to part (a). The answer to (b) is unique.
Solution to exercise 10-4-5
Figure 10.4.17.

10.4.6.7.

Answer.
Solution 1:
Basis: A binary tree consisting of a single vertex, which is a leaf, satisfies the equation \(\text{leaves} = \textrm{internal vertices} + 1\)
Induction:Assume that for some \(k\geq 1\text{,}\) all full binary trees with \(k\) or fewer vertices have one more leaf than internal vertices. Now consider any full binary tree with \(k+1\) vertices. Let \(T_A\) and \(T_B\) be the left and right subtrees of the tree which, by the definition of a full binary tree, must both be full. If \(i_A\) and \(i_B\) are the numbers of internal vertices in \(T_A\) and \(T_B\text{,}\) and \(j_A\) and \(j_B\) are the numbers of leaves, then \(j_A=i_A+1 \) and \(j_B=i_B+1\text{.}\) Therefore, in the whole tree,
\begin{equation*} \begin{split} \textrm{the number of leaves} & =j_A+j_B\\ &=\left(i_A+1\right)+\left(i_B+1\right)\\ &=\left(i_A+i_B+1\right)+1\\ &=(\textrm{number of internal vertices})+1 \end{split} \end{equation*}
Solution 2:
Imagine building a full binary tree starting with a single vertex. By continuing to add leaves in pairs so that the tree stays full, we can build any full binary tree. Our starting tree satisfies the condition that the number of leaves is one more than the number of internal vertices . By adding a pair of leaves to a full binary tree, an old leaf becomes an internal vertex, increasing the number of internal vertices by one. Although we lose a leaf, the two added leaves create a net increase of one leaf. Therefore, the desired equality is maintained.

10.4.6.8.

Solution.
  1. The root of \(B\) is the root of the corresponding ordered rooted tree, which as no siblings.
  2. Two columns of five graphs
    Figure 10.4.23.
  3. Two columns of five graphs
    Figure 10.4.24.
  4. The number of ordered rooted trees with \(n\) vertices is equal to the number of binary trees with \(n-1\) vertices, \(\frac{1}{n} \binom{2(n-1)}{n-1}\)

11 Algebraic Structures
11.1 Operations
11.1.4 Exercises

11.1.4.1.

Answer.
  1. Commutative, and associative. Notice that zero is the identity for addition, but it is not a positive integer.
  2. Commutative, associative, and has an identity (1)
  3. Commutative, associative, has an identity (1), and is idempotent
  4. Commutative, associative, and idempotent
  5. None. Notice that \(2 @ (3 @ 3) = 134217728\text{,}\) while \((2 @ 3) @ 3 = 512\text{;}\) and \(a @ 1 = a\text{,}\) while \(1 @ a = 1\text{.}\)

11.1.4.3.

Answer.
\begin{equation*} \begin{split} a, b \in A \cap B & \Rightarrow a, b \in A \textrm{ by the definition of intersection}\\ & \Rightarrow a*b \in A\textrm{ by the closure of } A \textrm{ with respect to } * \end{split} \end{equation*}
Similarly, \(a, b \in A \cap B \Rightarrow a*b \in B\text{.}\) Therefore, \(a * b \in A \cap B\text{.}\) The set of positive integers is closed under addition, and so is the set of negative integers, but \(1 + -1 = 0\text{.}\) Therefore, their union, the nonzero integers, is not closed under addition.

11.1.4.5.

Answer.
  1. \(*\) is commutative since \(\left| a-b\right| =\left| b-a\right|\) for all \(a, b \in \mathbb{N}\)
  2. \(*\) is not associative. Take \(a = 1\text{,}\) \(b = 2\text{,}\) and \(c = 3\text{,}\) then \((a * b) * c =\left| \left| 1-2\right| -3\right| =2\) , and \(a * (b * c) = \left| 1-\left| 2-3\right| \right| = 0\text{.}\)
  3. Zero is the identity for \(*\) on \(\mathbb{N}\text{,}\) since \(a*0=\left| a - 0\right| = a = \left| 0-a\right| = 0 * a.\)
  4. Each element of \(\mathbb{N}\) inverts itself since \(a * a=\left| a-a\right| = 0\text{.}\)
  5. \(*\) is not idempotent, since, for \(a\neq 0\text{,}\) \(a * a =0 \neq a\text{.}\)

11.2 Algebraic Systems
11.2.4 Exercises

11.2.4.1.

Answer.
The terms “generic” and “trade” for prescription drugs are analogous to “generic” and “concrete” algebraic systems. Generic aspirin, for example, has no name, whereas Bayer, Tylenol, Bufferin, and Anacin are all trade or specific types of aspirins. The same can be said of a generic group \([G; *]\) where \(G\) is a nonempty set and \(*\) is a binary operation on \(G\text{,}\) When examples of typical domain elements can be given along with descriptions of how operations act on them, such as \(\mathbb{Q}\)* or \(M_{2\times 2}(\mathbb{R})\text{,}\) then the system is concrete (has a specific name, as with the aspirin). Generic is a way to describe a general algebraic system, whereas a concrete system has a name or symbols making it distinguishable from other systems.

11.2.4.3.

Answer.
The systems in parts b, d, e, and f are groups.

11.2.4.5.

Answer.
  1. Elements are \(I=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{,}\) and \(T=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right)\text{,}\) the group is abelian. Operation table is \(\begin{array}{c|cc} \cdot & I & T\\ \hline I & I & T\\ T & T & I\\ \end{array}\)
  2. \begin{equation*} \begin{array}{c|c} & \begin{array}{cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3 \\ \end{array} \\ \hline \begin{array}{c} I \\ R_1 \\ R_2 \\ F_1 \\ F_2 \\ F_3 \\ \end{array} & \begin{array}{cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3 \\ R_1 & R_2 & I & F_2 & F_3 & F_1 \\ R_2 & I & R_1 & F_3 & F_1 & F_2 \\ F_1 & F_3 & F_2 & I & R_2 & R_1 \\ F_2 & F_1 & F_3 & R_1 & I & R_2 \\ F_3 & F_2 & F_1 & R_2 & R_1 & I \\ \end{array} \\ \end{array} \end{equation*}
    This group is non-abelian since, for example, \(F_1 F_2=R_2\) and \(F_2 F_1=R_1\text{.}\)
  3. 4! = 24, \(n!\text{.}\)

11.2.4.7.

Answer.
The identity is \(e\text{.}\) \(a*b = c\text{,}\) \(a*c= b\text{,}\) \(b*c = a\text{,}\) and \([V; *]\) is abelian. (This group is commonly called the Klein-4 group.)

11.2.4.8.

Solution.
Yes, this is a group. You might see some similarities with the group of three by three rook matrices.

11.3 Some General Properties of Groups
11.3.3 Exercises

11.3.3.1.

Answer.
  1. \(f\) is injective:
    \begin{equation*} \begin{split} f(x) = f(y) & \Rightarrow a * x = a * y \\ & \Rightarrow x = y\textrm{ by left cancellation}\\ \end{split}\text{.} \end{equation*}
    \(f\) is surjective: For all \(b \in G\text{,}\) \(f(x) = b\) has the solution \(a^{-1}*b\text{.}\)
  2. Functions of the form \(f(x) = a + x\text{,}\) where \(a\) is any integer, are bijections

11.3.3.3.

Answer.
Basis: (\(n = 2\)) \(\left(a_1*a_2\right)^{-1}= a_2^{-1}*a_1^{-1}\) by Theorem 11.3.7.
Induction: Assume that for some \(n \geq 2\text{,}\)
\begin{equation*} \left(a_1*a_2* \cdots *a_n\right)^{-1}=a_n^{-1}* \cdots * a_2^{-1}*a_1^{-1} \end{equation*}
We must show that
\begin{equation*} \left(a_1*a_2* \cdots *a_n*a_{n+1}\right)^{-1}=a_{n+1}^{-1}*a_n^{-1}* \cdots * a_2^{-1}*a_1^{-1} \end{equation*}
This can be accomplished as follows:
\begin{equation*} \begin{split} \left(a_1*a_2*\cdots *a_n*a_{n+1}\right)^{-1} &=\left(\left(a_1*a_2*\cdots *a_n\right)*a_{n+1}\right)^{-1}\textrm{ by the associative law}\\ &=a_{n+1}^{-1}*\left(a_1*a_2*\cdots *a_n\right)^{-1}\textrm{ by the basis}\\ &=a_{n+1}^{-1}*\left(a_n^{-1}*\cdots * a_2^{-1}*a_1^{-1}\right) \textrm{ by the induction hypothesis}\\ &= a_{n+1}^{-1}*a_n^{-1}*\cdots * a_2^{-1}*a_1^{-1} \textrm{ by the associative law}\\ \end{split} \end{equation*}

11.3.3.5.

Answer.
In this answer, we will refer to Lemma 11.3.13 simply as “the lemma.”
  1. Let \(p(n)\) be \(a^{-n}= \left(a^{-1}\right)^n\text{,}\) where \(a\) is any element of group \([G; *]\text{.}\) First we will prove that \(p(n)\) is true for all \(n \geq 0\text{.}\)
    Basis: If \(n = 0\text{,}\) Using the definition of the zero exponent, \(\left(a^0\right)^{-1} = e^{-1} = e\text{,}\) while \(\left(a^{-1}\right)^0= e\text{.}\) Therefore, \(p(0)\) is true.
    Induction: Assume that for some \(n \geq 0\text{,}\) \(p(n\)) is true.
    \begin{equation*} \begin{split} \left(a^{n+1}\right)^{-1} &= \left(a^n*a\right)^{-1}\textrm{ by the definition of exponentiation}\\ & =a^{-1}*\left(a^n\right)^{-1}\textrm{ by the lemma}\\ & = a^{-1}*\left(a^{-1}\right)^n\textrm{ by the induction hypothesis}\\ & = \left(a^{-1}\right)^{n+1} \textrm{ by the lemma} \end{split} \end{equation*}
    If \(n\) is negative, then \(-n\) is positive and
    \begin{equation*} \begin{split} a^{-n} & = \left(\left(\left(a^{-1}\right)^{-1}\right)^{-n} \right)\\ & =\left(a^{-1}\right)^{-(-n)}\textrm{ since the property is true for positive numbers}\\ & =\left(a^{-1}\right)^n \end{split} \end{equation*}
  2. For \(m > 1\text{,}\) let \(p(m)\) be \(a^{n+m}=a^n*a^m\) for all \(n\geq 1\text{.}\) The basis for this proof follows directly from the basis for the definition of exponentiation.
    Induction: Assume that for some \(m > 1\text{,}\) \(p(m)\) is true. Then
    \begin{equation*} \begin{split} a^{n+(m+1)}&= a^{(n+m)+1}\textrm{ by the associativity of integer addition}\\ &=a^{n+m}*a^1\textrm{ by the definition of exponentiation}\\ &=\left(a^n*a^m\right)*a^1 \textrm{ by the induction hypothesis}\\ &= a^n*\left(a^m*a^1\right)\textrm{ by associativity}\\ &= a^n*a^{m+1}\textrm{ by the definition of exponentiation} \end{split} \end{equation*}
    To complete the proof, you need to consider the cases where \(m\) and/or \(n\) are negative.
  3. Let \(p(m)\)be \(\left(a^n\right)^m= a^{n m}\) for all integers \(n\text{.}\)
    Basis: \(\left(a^m\right)^0= e\) and \(a^{m\cdot 0}=a^0= e\) therefore, \(p(0)\) is true.
    Induction; Assume that \(p(m)\) is true for some \(m >\)0,
    \begin{equation*} \begin{split} \left(a^n\right)^{m+1}&=\left(a^n\right)^m*a^n \textrm{ by the definition of exponentiation}\\ &=a^{n m}*a^n\textrm{ by the induction hypothesis}\\ & =a^{n m + n}\textrm{ by part (b) of this proof}\\ & =a^{n(m+1)} \end{split} \end{equation*}
    Finally, if \(m\) is negative, we can verify that \(\left(a^n\right)^m= a^{n m}\) using many of the same steps as the positive case.

11.4 Greatest Common Divisors and the Integers Modulo \(n\)
11.4.2 The Euclidean Algorithm

Investigation 11.4.1.

Solution.
If quotient in division is 1, then we get the slowest possible completion. If \(a = b + r\text{,}\) then working backwards, each remainder would be the sum of the two previous remainders. This described a sequence like the Fibonacci sequence and indeed, the greatest common divisor of two consecutive Fibonacci numbers will take the most steps to reach a final value of 1.

11.4.6 Exercises

11.4.6.1.

Answer.
  1. \(\displaystyle 2^2 \cdot 3 \cdot 5\)
  2. \(\displaystyle 3^2 \cdot 5\cdot 7\)
  3. \(\displaystyle 19^4\)
  4. 12112

11.4.6.3.

Answer.
  1. 2
  2. 5
  3. 0
  4. 0
  5. 2
  6. 2
  7. 1
  8. 3
  9. 0

11.4.6.5.

Answer.
  1. 1
  2. 1
  3. \(m(4) = r(4)\text{,}\) where \(m = 11 q + r\text{,}\) \(0 \leq r < 11\)

11.4.6.7.

Answer.
Since the solutions, if they exist, must come from \(\mathbb{Z}_2\text{,}\) substitution is the easiest approach.
  1. 1 is the only solution, since \(1^2+_21=0\) and \(0^2+_21=1\)
  2. No solutions, since \(0^2+_2 0+_2 1=1\text{,}\) and \(1^2+_2 1+_2 1=1\)

11.4.6.10.

Hint.
Prove by induction on \(m\) that you can divide any positive integer into \(m\text{.}\) That is, let \(p(m)\) be “For all \(n\) greater than zero, there exist unique integers \(q\) and \(r\) such that \(\dots\) .” In the induction step, divide \(n\) into \(m - n\text{.}\)

11.4.6.11.

Solution.
The given conditions can be converted to a system of linear equations:
\begin{equation*} \begin{array}{c} f(1)=11 \Rightarrow a +_{17} b = 11\\ f(2)=4 \Rightarrow 2 \times_{17} a +_{17} b =4\\ \end{array} \end{equation*}
If we subtract the first equation from the second, we get \(a = 4 +_{17} (-11) = 4 +_{17} 6= 10\text{.}\) This implies that \(b=1\text{,}\) and \(f(i) = 10\times+{17}i + 1\text{.}\) To get a formula for the inverse of \(f\) we solve \(f(j)=i\) for \(j\text{,}\) using the fact that the multiplicative inverse of 10 (mod 17) is 12.
\begin{equation*} \begin{split} f(j)=i & \Rightarrow 10\times+{17}j + 1 = i\\ & \Rightarrow 10\times+{17}j = i +_{17} 16\\ & \Rightarrow j = 12\times_{17}( i +_{17} 16)\\ \end{split} \end{equation*}
Therefore \(f^{-1}(i) = 12\times_{17}( i +_{17} 16) = 12\times_{17} i +_{17} 5\text{.}\)

11.4.6.12.

Solution.
This system is a monoid with identity 6 (surprise!). However it is not a group since 0 has no inverse.

11.4.6.13.

Solution.
By Bézout’s lemma, \(450\) is an element of \(\mathbb{U}_{2021}\text{.}\) It’s inverse in the group is \(759\) because
\begin{equation*} 450 \cdot 759 = 2021\cdot 169 +1 \quad \Rightarrow \quad 450 \times_{2021} 759 =1. \end{equation*}

11.5 Subsystems
11.5.5 Exercises

11.5.5.1.

Answer.
Only a and c are subgroups.

11.5.5.3.

Answer.
\(\left\{I,R_1,R_2\right\}\text{,}\) \(\left\{I,F_1\right\}\text{,}\) \(\left\{I,F_2\right\}\text{,}\) and \(\left\{I,F_3\right\}\) are all the proper subgroups of \(R_3\text{.}\)

11.5.5.5.

Answer.
  1. \(\langle 1\rangle = \langle 5\rangle = \mathbb{Z}_6\text{,}\) \(\quad\)\(\langle 2\rangle = \langle 4\rangle = \{2, 4, 0\}\text{,}\) \(\langle 3\rangle = \{3, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
  2. \(\langle 1\rangle = \langle 5\rangle = \langle 7\rangle = \langle 11\rangle =\mathbb{Z}_{12}\text{,}\) \(\langle 2\rangle = \langle 10\rangle = \{2, 4, 6, 8, 10, 0\}\text{,}\) \(\langle 3\rangle = \langle 9\rangle = \{3, 6, 9, 0\}\text{,}\) \(\langle 4\rangle = \langle 8 \rangle = \{ 4 , 8, 0\}\text{,}\) \(\langle 6\rangle = \{6, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
  3. \(\langle 1\rangle = \langle 3\rangle = \langle 5 \rangle = \langle 7\rangle = \mathbb{Z}_8\text{,}\) \(\langle 2\rangle = \langle 6\rangle = \{2, 4, 6, 0\}\text{,}\) \(\langle 4\rangle = \{4, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
  4. Based on the ordering diagrams for parts a through c in Figure 11.5.13, we would expect to see an ordering diagram similar to the one for divides on \(\{1, 2, 3, 4, 6, 8, 12, 24\}\) (the divisors of 24) if we were to examine the subgroups of \(\mathbb{Z}_{24}\text{.}\) This is indeed the case.
Figure for exercise 5 of Section 11.5
Figure 11.5.13. Figure for exercise 5

11.5.5.7.

Hint.
Use an indirect argument.
Answer.
Assume that \(H\) and \(K\) are subgroups of group \(G\text{,}\) and that, as in Figure 11.5.12, there are elements \(x \in H - K\) and \(y \in K - H\text{.}\) Consider the product \(x * y\text{.}\) Where could it be placed in the Venn diagram? If we can prove that it must lie in the outer region, \(H^c \cap K^c=(H \cup K)^c\text{,}\) then we have proven that \(H \cup K\) is not closed under \(*\) and cannot be a subgroup of \(G\text{,}\) Assume that \(x*y\in H\text{.}\) Since \(x\) is in \(H\text{,}\) \(x^{-1}\) is in \(H\) and so by closure \(x^{-1}*(x * y )= y \in H\) which is a contradiction. Similarly, \(x*y \notin K\text{.}\)
One way to interpret this theorem is that no group is the union of two groups.

11.6 Direct Products
11.6.3 Exercises

11.6.3.1.

Answer.
Table of \(\mathbb{Z}_2\times \mathbb{Z}_3\text{:}\)
\begin{equation*} \begin{array}{c|cccccc} +&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\ \hline (0,0)&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\ (0,1)&(0,1)&(0,2)&(0,0)&(1,1)&(1,2)&(1,0)\\ (0,2)&(0,2)&(0,0)&(0,1)&(1,2)&(1,0)&(1,1)\\ (1,0)&(1,0)&(1,1)&(1,2)&(0,0)&(0,1)&(0,2)\\ (1,1)&(1,1)&(1,2)&(1,0)&(0,1)&(0,2)&(0,0)\\ (1,2)&(1,2)&(1,0)&(1,1)&(0,2)&(0,0)&(0,1) \end{array} \end{equation*}
The only two proper subgroups are \(\{(0, 0), (1, 0)\}\) and \(\{(0, 0), (0, 1), (0, 2)\}\)

11.6.3.3. Algebraic properties of the \(n\)-cube.

Answer.
  1. (i) \(a + b \textrm{ could be }(1, 0) \textrm{ or } (0, 1)\text{.}\) (ii) \(a + b = (1, 1)\text{.}\)
  2. (i) \(a + b \textrm{ could be}(1, 0, 0), (0, 1, 0), \textrm{ or }(0, 0, 1)\text{.}\) (ii) \(a + b = (1, 1, 1)\text{.}\)
  3. (i) \(a + b\) has exactly one 1. (ii) \(a + b\) has all \(1's\text{.}\)

11.6.3.5.

Answer.
  1. No, 0 is not an element of \(\mathbb{Z} \times \mathbb{Z}\text{.}\)
  2. Yes.
  3. No, (0, 0) is not an element of this set.
  4. No, the set is not closed: \((1, 1) + (2, 4) = (3, 5)\) and \((3, 5)\) is not in the set.
  5. Yes.

11.7 Isomorphisms
11.7.4 Exercises

11.7.4.1.

Answer.
  1. Yes, \(f(n, x) = (x, n)\) for \((n, x) \in \mathbb{Z} \times \mathbb{R}\) is an isomorphism.
  2. No, \(\mathbb{Z}_2\times \mathbb{Z}\) has a two element subgroup while \(\mathbb{Z} \times \mathbb{Z}\) does not.
  3. No. \(\mathbb{Q} \times \mathbb{Q}\) is countable and \(\mathbb{R}\) is not. Therefore, no bijection can exist between them.
  4. Yes.
  5. No.
  6. Yes, one isomorphism is defined by \(f\left(a_1, a_2,a_3,a_4\right)=\left( \begin{array}{cc} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} \right)\text{.}\)
  7. Yes, one isomorphism is defined by \(f\left(a_1,a_2\right)=\left(a_1,10^{a_2}\right)\text{.}\)
  8. Yes.
  9. Yes \(f(k) = k(1,1)\text{.}\)

11.7.4.3.

Answer.
Consider three groups \(G_1\text{,}\) \(G_2\text{,}\) and \(G_3\) with operations \(*, \diamond , \textrm{ and } \star \text{,}\) respectively. We want to show that if \(G_1\) is isomorphic to \(G_2\text{,}\) and if \(G_2\) is isomorphic to \(G_3\) , then \(G_1\) is isomorphic to \(G_3\text{.}\)
\begin{equation*} G_1 \textrm{ isomorphic} \textrm{ to } G_2\Rightarrow \textrm{ there} \textrm{ exists} \textrm{ an} \textrm{ isomorphism } f:G_1\to G_2 \end{equation*}
\begin{equation*} G_2 \textrm{ isomorphic} \textrm{ to } G_3\Rightarrow \textrm{ there} \textrm{ exists} \textrm{ an} \textrm{ isomorphism } g:G_2\to G_3 \end{equation*}
If we compose \(g\) with \(f\text{,}\) we get the function \(g\circ f:G_1\to G_3\text{,}\) By Theorem 7.3.6 and Theorem 7.3.7, \(g\circ f\) is a bijection, and if \(a,b\in G_1\text{,}\)
\begin{equation*} \begin{split} (g\circ f)(a*b) &=g(f(a*b))\\ &=g(f(a)\diamond f(b))\quad \textrm{ since } f \textrm{ is an isomorphism}\\ & =g(f(a))\star g(f(b))\quad \textrm{ since } g \textrm{ is an isomorphism}\\ & =(g\circ f)(a) \star (g\circ f)(b) \end{split} \end{equation*}
Therefore, \(g\circ f\) is an isomorphism from \(G_1\) into \(G_3\text{,}\) proving that “is isomorphic to” is transitive.

11.7.4.5.

Answer.
By Theorem 11.7.14(a), \(T(0)\) must be 1. \(T(2)=T(1+_4 1)=T(1)\times_5 T(1) = 3 \times_5 3 = 4\text{.}\) Since \(T\) is a bijection, \(T(3)=2\text{.}\)

11.7.4.7.

Answer.
Let \(G\) be an infinite cyclic group generated by \(a\text{.}\) Then, using multiplicative notation, \(G=\left\{\left.a^n\right| n\in \mathbb{Z}\right\}\text{.}\) The map \(T: G \rightarrow \mathbb{Z}\) defined by \(T\left(a^n\right)=n\) is an isomorphism. This is indeed a function, since \(a^n=a^m\) implies \(n =m\text{.}\) Otherwise, \(a\) would have a finite order and would not generate \(G\text{.}\)
  1. \(T\) is one-to-one, since \(T\left(a^n\right) = T\left(a^m\right)\) implies \(n = m\text{,}\) so \(a^n= a^m\text{.}\)
  2. \(T\) is onto, since for any \(n\in \mathbb{Z}\text{,}\) \(T\left(a^n\right) = n\text{.}\)
  3. \(\displaystyle T\left(a^n*a^m \right) = T\left(a^{n+m}\right) =n + m\ =T\left(a^n\right)+T\left(a^m\right)\)

11.7.4.11.

Answer.
\(\mathbb{Z}_8\text{,}\) \(\mathbb{Z}_2\times \mathbb{Z}_4\) , and \(\mathbb{Z}_2^3\text{.}\) One other is the fourth dihedral group, introduced in Section 15.3.

11.7.4.13.

Answer.
Each 3 is the order of an element whose inverse is it’s square; i. e., if \(a\) has order 3, \(a^2=a^{-1}\) is distinct from \(a\) and also has order 3 and contributes a second matching 3.

12 More Matrix Algebra
12.1 Systems of Linear Equations
12.1.7 Exercises

12.1.7.1.

Answer.
  1. \(\displaystyle \{(4/3, 1/3)\}\)
  2. \(\displaystyle \{(\frac{1}{2}x_3-3, -4 x_3 +11,x_3) \mid x_3 \in \mathbb{R}\} \)
  3. \(\displaystyle \{(-5, 14/5, 8/5)\}\)
  4. \(\displaystyle \left\{\left(6.25 - 2.5x_3, -0.75 + 0.5x_3 , x_3\right) \mid x_3 \in \mathbb{R}\right\}\)

12.1.7.3.

Answer.
  1. Basic variables: \(x_1\text{,}\) \(x_2\) and \(x_4\text{.}\) Free variable: \(x_3\text{.}\) Solution set: \(\{(1.2+5x_3, 2.6-4 x_3, 4.5) \mid x_3 \in \mathbb{R}\}\)
  2. Basic variables: \(x_1\) and \(x_2\text{.}\) Free variable: \(x_3\text{.}\) The solution set is empty because the last row of the matrix converts to the inconsistent equation \(0=1\text{.}\)
  3. Basic variables: \(x_1\) and \(x_2\text{.}\) Free variable: \(x_3\text{.}\) Solution set: \(\left\{\left(-6 x_3 + 5, 2 x_3+1, x_3 \right) \mid x_3 \in \mathbb{R}\right\}\)
  4. Basic variables: \(x_1\text{,}\) \(x_2\) and \(x_3\text{.}\) Free variable: \(x_4\text{.}\) Solution set: \(\left\{\left(3 x_4 + 1, -2x_4 + 2, x_4 + 1, x_4\right) \mid x_4 \in \mathbb{R}\right\}\)

12.1.7.5.

Answer.
  1. \(\displaystyle \{(3,0)\}\)
  2. \(\displaystyle \{(3,0,4)\}\)

12.1.7.7.

Answer.
Proof: Since \(b\) is the \(n\times 1\) matrix of 0{’}s, let’s call it \(\pmb{0}\text{.}\) Let S be the set of solutions to \(A X = \pmb{0}\text{.}\) If \(X_1\) and \(X_2\) be in \(S\text{.}\) Then
\begin{equation*} A\left(X_1 + X_2 \right) = A X_1 + A X_2 = \pmb{0} + \pmb{0} = \pmb{0} \end{equation*}
so \(X_1+ X_2 \in S\text{;}\) or in other words, \(S\) is closed under addition in \(\mathbb{R}^n\text{.}\)
The identity of \(\mathbb{R}^n\) is \(\pmb{0}\text{,}\) which is in \(S\text{.}\) Finally, let \(X\) be in\(S\text{.}\) Then
\begin{equation*} A(-X) = -(A X) = - \pmb{0} = \pmb{0} \end{equation*}
and so \(-X\) is also in \(S\text{.}\)

12.2 Matrix Inversion
12.2.3 Exercises

12.2.3.3.

Answer.
  1. \(\displaystyle \left( \begin{array}{cc} \frac{15}{11} & \frac{30}{11} \\ \frac{3}{11} & -\frac{5}{11} \\ \end{array} \right)\)
  2. \(\displaystyle \left( \begin{array}{ccc|c} -20 & \frac{21}{2} & \frac{9}{2} & -\frac{3}{2} \\ 2 & -1 & 0 & 0 \\ -4 & 2 & 1 & 0 \\ 7 & -\frac{7}{2} & -\frac{3}{2} & \frac{1}{2} \\ \end{array} \right)\)
  3. The inverse does not exist. When the augmented matrix is row-reduced (see below), the last row of the first half cannot be manipulated to match the identity matrix.
  4. \(\displaystyle \left( \begin{array}{ccc} 1 & 0 & 0 \\ -3 & 1 & 1 \\ -4 & 1 & 2 \\ \end{array} \right)\)
  5. The inverse does not exist.
  6. \(\displaystyle \left( \begin{array}{ccc} 9 & -36 & 30 \\ -36 & 192 & -180 \\ 30 & -180 & 180 \\ \end{array} \right)\)

12.2.3.5.

Answer.
The solutions are in the solution section of Section 12.1, exercise 1, We illustrate with the outline of the solution to part (c). The matrix version of the system is
\begin{equation*} \left( \begin{array}{ccc} 1 & 1 & 2 \\ 1 & 2 & -1 \\ 1 & 3 & 1 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 1 \\ -1 \\ 5 \\ \end{array} \right) \end{equation*}
We compute the inverse of the matrix of coefficients and get
\begin{equation*} A^{-1}=\left( \begin{array}{ccc} 1 & 1 & 2 \\ 1 & 2 & -1 \\ 1 & 3 & 1 \\ \end{array} \right)^{-1}=\frac{1}{5}\left( \begin{array}{ccc} 5 & 5 & -5 \\ -2 & -1 & 3 \\ 1 & -2 & 1 \\ \end{array} \right) \end{equation*}
and
\begin{equation*} \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=A^{-1}\left( \begin{array}{c} 1 \\ -1 \\ 5 \\ \end{array} \right)=\left( \begin{array}{c} -5 \\ \frac{14}{5} \\ \frac{8}{5} \\ \end{array} \right) \end{equation*}

12.3 An Introduction to Vector Spaces
12.3.3 Exercises

12.3.3.3.

Answer.
The dimension of \(M_{2\times 3}(\mathbb{R})\) is 6 and yes, \(M_{m\times n}(\mathbb{R})\) is also a vector space of dimension \(m \cdot n\text{.}\) One basis for \(M_{m\times n}(\mathbb{R})\) is \(\{A_{ij} \mid 1 \leq i \leq m, 1 \leq j \leq n\}\) where \(A_{ij}\) is the \(m\times n\) matrix with entries all equal to zero except for in row \(i\text{,}\) column \(j\) where the entry is 1.

12.3.3.7.

Answer.
If the matrices are named \(B\text{,}\) \(A_1\text{,}\) \(A_2\) , \(A_3\text{,}\) and \(A_4\) , then
\begin{equation*} B = \frac{8}{3}A_1 + \frac{5}{3}A_2+\frac{-5}{3}A_3+\frac{23}{3}A_4 \end{equation*}

12.3.3.9.

Answer.
  1. If \(x_1 = (1, 0)\text{,}\) \(x_2= (0, 1)\text{,}\) and \(y = \left(b_1, b_2\right)\text{,}\) then \(y = b_1x_1+b_2x_2\text{.}\) If \(x_1 = (3, 2)\text{,}\) \(x_2= (2,1)\text{,}\) and \(y = \left(b_1, b_2\right)\text{,}\) then \(y =\left(- b_1+2b_2\right)x_1+\left(2b_1-3b_2\right)x_2\text{.}\)
  2. If \(y = \left(b_1, b_2\right)\) is any vector in \(\mathbb{R}^2\) , then \(y =\left(- 3b_1+4b_2\right)x_1+\left(-b_1+b_2\right)x_2 + (0)x_3\)
  3. One solution is to add any vector(s) to \(x_1\text{,}\) \(x_2\text{,}\) and \(x_3\) of part b.
  4. 2, \(n\)
  5. \(\displaystyle \left( \begin{array}{cc} x & y \\ z & w \\ \end{array} \right)= x A_1+y A_2+ z A_3+ w A_4\)
  6. \(a_0+a_1x + a_2x^2+ a_3x^3=a_0(1)+a_1(x) + a_2\left(x^2\right)+ a_3\left(x^3\right)\text{.}\)

12.3.3.11.

Answer.
  1. The set is linearly independent: let \(a\) and \(b\) be scalars such that \(a(4, 1) + b(1, 3) = (0, 0)\text{,}\) then \(4a + b = 0\textrm{ and } a + 3b= 0\) which has \(a = b = 0\) as its only solutions. The set generates all of \(\mathbb{R}^2\text{:}\) let \((a, b)\) be an arbitrary vector in \(\mathbb{R}^2\) . We want to show that we can always find scalars \(\beta _1\) and \(\beta _2\) such that \(\beta _1(4, 1) +\beta _2 (1,3) = (a, b)\text{.}\) This is equivalent to finding scalars such that \(4\beta _1 +\beta _2 = a\) and \(\beta _1 + 3\beta _2 = b\text{.}\) This system has a unique solution \(\beta _1=\frac{3a - b}{11}\text{,}\) and \(\beta _2= \frac{4b-a}{11}\text{.}\) Therefore, the set generates \(\mathbb{R}^2\text{.}\)

12.3.3.13.

Answer.
The answer to the last part is that the three vector spaces are all isomorphic to one another. Once you have completed part (a) of this exercise, the following translation rules will give you the answer to parts (b) and (c),
\begin{equation*} (a,b,c,d) \leftrightarrow \left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right)\leftrightarrow a + b x+c x^2+ d x^2 \end{equation*}

12.4 The Diagonalization Process
12.4.4 Exercises

12.4.4.1.

Answer.
  1. Any nonzero multiple of \(\left( \begin{array}{c} 1 \\ -1 \\ \end{array} \right)\) is an eigenvector associated with \(\lambda =1\text{.}\)
  2. Any nonzero multiple of \(\left( \begin{array}{c} 1 \\ 2 \\ \end{array} \right)\) is an eigenvector associated with \(\lambda =4\text{.}\)
  3. Let \(x_1=\left( \begin{array}{c} a \\ -a \\ \end{array} \right)\) and \(x_2=\left( \begin{array}{c} b \\ 2b \\ \end{array} \right)\) . You can verify that \(c_1x_1+ c_2x_2=\left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right)\) if and only if \(c_1= c_2= 0.\) Therefore, \(\left\{x_1,x_2\right\}\) is linearly independent.

12.4.4.3.

Answer.
Part c: You should obtain \(\left( \begin{array}{cc} 4 & 0 \\ 0 & 1 \\ \end{array} \right)\) or \(\left( \begin{array}{cc} 1 & 0 \\ 0 & 4 \\ \end{array} \right)\text{,}\) depending on how you order the eigenvalues.

12.4.4.5.

Answer.
  1. If \(P=\left( \begin{array}{cc} 2 & 1 \\ 3 & -1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 4 & 0 \\ 0 & -1 \\ \end{array} \right)\text{.}\)
  2. If \(P=\left( \begin{array}{cc} 1 & 1 \\ 7 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 5 & 0 \\ 0 & -1 \\ \end{array} \right)\text{.}\)
  3. If \(P=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 3 & 0 \\ 0 & 4 \\ \end{array} \right)\text{.}\)
  4. If \(P=\left( \begin{array}{ccc} 1 & -1 & 1 \\ -1 & 4 & 2 \\ -1 & 1 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{ccc} -2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\text{.}\)
  5. \(A\) is not diagonalizable. Five is a double root of the characteristic equation, but has an eigenspace with dimension only 1.
  6. If \(P=\left( \begin{array}{ccc} 1 & 1 & 1 \\ -2 & 0 & 1 \\ 1 & -1 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\text{.}\)

12.4.4.7.

Answer.
This is a direct application of the definition of matrix multiplication. Let \(A_{(i)}\) be the \(i^{\textrm{th}}\) row of \(A\text{,}\) and let \(P^{(j)}\) be the \(j^{\textrm{th}}\) column of \(P\text{.}\) Then the \(j^{\textrm{th}}\) column of the product \(A P\) is
\begin{equation*} \left( \begin{array}{c} A_{(1)}P^{(j)} \\ A_{(2)}P^{(j)} \\ \vdots \\ A_{(n)}P^{(j)} \\ \end{array} \right) \end{equation*}
Hence, \((AP)^{(j)}= A\left(P^{(j)}\right)\) for \(j =1,2,\ldots , n\text{.}\) Thus, each column of \(A P\) depends on \(A\) and the \(j^{\textrm{ th}}\) column of \(P\text{.}\)

12.5 Some Applications
12.5.5 Exercises

12.5.5.4.

Hint.
The characteristic polynomial of the adjacency matrix is \(\lambda ^4 - 4 \lambda^2\text{.}\)

12.5.5.5.

Answer.
  1. Since \(A=A^1= \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ \end{array} \right)\text{,}\) there are 0 paths of length 1 from: node c to node a, node b to node b, and node a to node c; and there is 1 path of length 1 for every other pair of nodes.
  2. The characteristic polynomial is \(\lvert A-c I\rvert = \left| \begin{array}{ccc} 1-c & 1 & 0 \\ 1 & -c & 1 \\ 0 & 1 & 1-c \\ \end{array} \right| = -c^3+2 c^2+c-2\)
    Solving the characteristic equation \(-c^3+2 c^2+c-2=0\) we find solutions 1, 2, and -1.
    If \(c=1\text{,}\) we find the associated eigenvector by finding a nonzero solution to \(\left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 0 & 1 & 0 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) One of these, which will be the first column of \(P\text{,}\) is \(\left( \begin{array}{c} 1 \\ 0 \\ -1 \\ \end{array} \right)\)
    If \(c=2\text{,}\) the system \(\left( \begin{array}{ccc} -1 & 1 & 0 \\ 1 & -2 & 1 \\ 0 & 1 & -1 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) yields eigenvectors, including \(\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right)\text{,}\) which will be the second column of \(P\text{.}\)
    If \(c = -1\text{,}\) then the system determining the eigenvectors is \(\left( \begin{array}{ccc} 2 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) and we can select \(\left( \begin{array}{c} 1 \\ -2 \\ 1 \\ \end{array} \right)\text{,}\) although any nonzero multiple of this vector could be the third column of \(P\text{.}\)
  3. Assembling the results of part (b) we have \(P=\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & -2 \\ -1 & 1 & 1 \\ \end{array} \right)\) .
    \begin{equation*} \begin{split} A^4 & = P \left( \begin{array}{ccc} 1^4 & 0 & 0 \\ 0 & 2^4 & 0 \\ 0 & 0 & (-1)^{4 } \\ \end{array} \right)P^{-1}= P \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 1 \\ \end{array} \right)P^{-1}\\ &=\left( \begin{array}{ccc} 1 & 16 & 1 \\ 0 & 16 & -2 \\ -1 & 16 & 1 \\ \end{array} \right)\left( \begin{array}{ccc} \frac{1}{2} & 0 & -\frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \end{array} \right)\\ &=\left( \begin{array}{ccc} 6 & 5 & 5 \\ 5 & 6 & 5 \\ 5 & 5 & 6 \\ \end{array} \right)\\ \end{split} \end{equation*}
    Hence there are five different paths of length 4 between distinct vertices, and six different paths that start and end at the same vertex. The reader can verify these facts from Figure 12.5.4

12.5.5.7.

Answer.
  1. \(e^A=\left( \begin{array}{cc} e & e \\ 0 & 0 \\ \end{array} \right)\) , \(e^B=\left( \begin{array}{cc} 0 & 0 \\ 0 & e^2 \\ \end{array} \right)\text{,}\) and \(e^{A+B}=\left( \begin{array}{cc} e & e^2-e \\ 0 & e^2 \\ \end{array} \right)\)
  2. Let \(\pmb{0}\) be the zero matrix, \(e^{\pmb{0}}=I + \pmb{0}+\frac{\pmb{0}^2}{2}+\frac{\pmb{0}^3}{6}+\ldots =I\) .
  3. Assume that \(A\) and \(B\) commute. We will examine the first few terms in the product \(e^A e^B\text{.}\) The pattern that is established does continue in general. In what follows, it is important that \(A B = B A\text{.}\) For example, in the last step, \((A+B)^2\) expands to \(A^2+A B + B A + B^2\text{,}\) not \(A^2+ 2 A B + B^2\text{,}\) if we can’t assume commutativity.
    \begin{equation*} \begin{split} e^Ae^B &= \left(\sum _{k=0}^{\infty } \frac{A^k}{k!}\right) \left(\sum _{k=0}^{\infty } \frac{B^k}{k!}\right)\\ & =\left(I + A+\frac{A^2}{2}+ \frac{A^3}{6}+ \cdots \right)\left(I +B+\frac{B^2}{2}+ \frac{B^3}{6}+ \cdots \right)\\ &= I + A + B+ \frac{A^2}{2}+ A B + \frac{B^2}{2}+\frac{A^3}{6}+ \frac{A^2B}{2}+\frac{A B^2}{2}+ \frac{B^3}{6}+\cdots \\ &= I + (A+B) + \frac{1}{2}\left(A^2+ 2 A B + B^2\right)+ \frac{1}{6}\left(A^3+ 3A^2B+ 3A B^2+ B^3\right)+\cdots \\ &=I + (A+B)+ \frac{1}{2}(A+B)^2+ \frac{1}{6}(A+B)^3+\cdots \\ & =e^{A+B}\\ \end{split} \end{equation*}
  4. Since \(A\) and \(-A\) commute, we can apply part d;
    \begin{equation*} e^Ae^{-A} = e^{A+(-A)} =e^{\pmb{0}} =I \end{equation*}

12.6 Linear Equations over the Integers Mod 2
12.6.2 Exercises

12.6.2.1.

Answer.
  1. \(\displaystyle \{(0,0,0),(1,1,1)\}\)
  2. \(\displaystyle \{(1,1,1,0)\}\)

12.6.2.2.

Answer.
As suggested here is the augmented matrix with both right sides, and its row reduction:
\begin{equation*} \begin{split} \left( \begin{array}{cccc|cc} 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ \end{array} \right) & \text{ }\longrightarrow \text{ } \left( \begin{array}{cccc|cc} \textbf{1} & 0 & 1 & 1 & 0 & 0 \\ 0 & \textbf{1} & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right)\\ \end{split} \end{equation*}
There are only two basic variables here because the left side of the last equation is the sum of the left sides of the first two equations.
  1. Ignoring the last column of both matrices, we see that the last equation of the first system reduces to \(0=0\text{,}\) which is always true, and the first two equations yield two free variables, \(x_3\) and \(x_4\text{.}\) The general solution is the set of quadruples \(\{(x_3 +_2 x_4,x_3 +_2 1, x_3, x_4) \mid x_3, x_4 \in \mathbb{Z}_2 \}\text{.}\) The cardinality of the solution set is 4.
  2. If we replace the fifth column with the sixth one, the last row indicates that \(0=1\text{,}\) which means that the solution set is empty.

12.6.2.3.

Answer.
  1. Row reduction produces a solution with one free variable, \(x_3\text{.}\)
    \begin{equation*} \begin{split} (x_1, x_2, x_3, x_4, x_5)& =(x_3,x_3,x_3,0,0)\\ & = x_3 (1,1,1,0,0) \\ \end{split} \end{equation*}
    The solution set has only two elements. It is \(\{(0,0,0,0,0), (1,1,1,0,0)\}\text{.}\) Since \(\mathbb{Z}_{2}^{5}\) is a finite group, the solution set is a subgroup because it is closed with respect to coordinatewise mod 2 addition.
  2. The row-reduced augmented matrix of coefficients provides the solution
    \begin{equation*} \begin{split} (x_1, x_2, x_3, x_4, x_5)& =(x_3,1+x_3,x_3,1,0)\\ & = (0,1,0,1,0) + x_3 (1,1,1,0,0) \\ \end{split} \end{equation*}
    Therefore, the solution to this system is a shift of the solution set to the homogeneous system by the vector \((0,1,0,1,0)\text{,}\) which is \(\{(0,1,0,1,0), (1,0,1,1,0)\}\)

13 Boolean Algebra
13.1 Posets Revisited

Exercises

13.1.1.
Answer.
  1. 1, 5
  2. 5
  3. 30
  4. 30
  5. See the Sage cell below with the default input displaying a Hasse diagram for \(D_{12}\text{.}\)
13.1.3.
Answer.
  • Solution for Hasse diagram (b):
    • \begin{equation*} \begin{array}{c|c} \begin{array}{c|ccccc} \lor &a_1 & a_2 & a_3 & a_4 & a_5 \\ \hline a_1 & a_1 &a_2 & a_3 & a_4 & a_5 \\ a_2 & a_2 & a_2 & a_4 & a_4 & a_5 \\ a_3 &a_3 & a_4 & a_3 & a_4 & a_5 \\ a_4 & a_4 & a_4 & a_4 & a_4 & a_5 \\ a_5 & a_5 & a_5 & a_5 & a_5 & a_5 \\ \end{array} &\quad \begin{array}{c|ccccc} \land & a_1 & a_2 & a_3 & a_4 & a_5 \\\hline a_1 & a_1 & a_1 & a_1 & a_1 & a_1 \\ a_2 & a_1 & a_2 & a_1 & a_2 & a_2 \\ a_3 & a_1 & a_1 & a_3 & a_3 & a_3 \\ a_4 & a_1 & a_2 & a_3 & a_4 & a_4 \\ a_5 & a_1 & a_2 & a_3 & a_4 & a_5 \\ \end{array} \end{array} \end{equation*}
      \(a_1\) is the least element and \(a_5\) is the greatest element.
  • Partial solution for Hasse diagram (f):
    • \(\textrm{ lub}\left(a_2, a_3\right)\) and \(\textrm{ lub}\left( a_4,a_5\right)\) do not exist.
    • No greatest element exists, but \(a_1\) is the least element.
13.1.5.
Answer.
If \(0\) and \(0'\) are distinct least elements, then
\begin{equation*} \left. \begin{array}{cc} 0\leq 0' & \textrm{ since } 0 \textrm{ is a least element} \\ 0'\leq 0 & \textrm{ since } 0' \textrm{ is a least element} \\ \end{array} \right\}\Rightarrow 0=0' \textrm{ by antisymmetry, a contradiction} \end{equation*}
13.1.7.
Answer.
  1. The sum of elements in \(A \cap B =\{2,3,6\}\) is odd and disqualifies the set from being an element of the poset.
  2. The following correctly complete the statements in this part.
    1. \(\dots A \subseteq R\) and \(B \subseteq R\)
    2. \(\dots\) for all \(A \in \mathcal{P}_0\text{,}\) \(R \subseteq A\)
  3. Any set that contains the union of \(A\cup B=\{1,2,3,6,7\}\) but also contains 3 or 5, but not both will be an upper bound. You can create several by including on not including 4 or 8.
  4. The least upper bound doesn’t exist. Notice that the union of \(A\) and \(B\) isn’t in \(\mathcal{P}_0\text{.}\) One of the two sets \(\{1,2,3,5,6,7\}\) and \(\{1,2,3,6,7,9\}\) is contained within every upper bound of \(A\) and \(B\) but neither is contained within the other.

13.2 Lattices

Exercises

13.2.5.
Answer.
One reasonable definition would be this: Let \([L; \lor, \land ]\) be a lattice and let \(K\) be a nonempty subset of \(L\text{.}\) Then \(K\) is a sublattice of \(L\) if and only if \(K\) is closed under both \(\lor\) and \(\land\)

13.3 Boolean Algebras

Exercises

13.3.1.
Answer.
\(\begin{array}{cc} B & \textrm{ Complement of } B \\ \hline \begin{array}{c} \emptyset \\ \{a\} \\ \{b\} \\ \{c\} \\ \{a,b\} \\ \{a,c\} \\ \{b,c\} \\ A \\ \end{array} & \begin{array}{c} A \\ \{b,c\} \\ \{a,c\} \\ \{a,b\} \\ \{c\} \\ \{b\} \\ \{a\} \\ \emptyset \\ \end{array} \\ \end{array}\)
This lattice is a Boolean algebra since it is a distributive complemented lattice.
13.3.3.
Answer.
a and g.
13.3.5.
Answer.
  1. \(\displaystyle S^*:a \lor b= a \textrm{ if } a \geq b\)
  2. The dual of \(S:A\cap B = A\textrm{ if }A \subseteq B\) is \(S^*:A \cup B = A\textrm{ if } A \supseteq B\)
  3. Yes
  4. The dual of \(S:p \land q\Leftrightarrow p\textrm{ }\textrm{ if } p\Rightarrow q\) is \(S^*:p \lor q\Leftrightarrow p \textrm{ if } q\Rightarrow p\)
  5. Yes
13.3.7.
Answer.
\([B; \land, \lor, -]\) is isomorphic to \([B';\land, \lor, \tilde{}]\) if and only if there exists a function \(T:B \to B'\) such that
  1. \(T\) is a bijection;
  2. \(\displaystyle T(a\land b)=T(a)\land T(b)\quad \textrm{ for} \textrm{ all } a,b\in B\)
  3. \(\displaystyle T(a\lor b)=T(a)\lor T(b)\quad \textrm{ for} \textrm{ all } a, b \in B\)
  4. \(T(\bar{a})=\tilde{T(a)}\quad \textrm{ for all } a\in B\text{.}\)

13.4 Atoms of a Boolean Algebra

Exercises

13.4.1.
Answer.
  1. For \(a = 3\) we must show that for each \(x \in D_{30}\) one of the following is true: \(x\land 3=3\) or \(x\land 3=1\text{.}\) We do this through the following table:
    \begin{equation*} \begin{array}{cc} x & \textrm{ verification} \\ \hline \begin{array}{c} 1 \\ 2 \\ 3 \\ 5 \\ 6 \\ 10 \\ 15 \\ 30 \\ \end{array} & \begin{array}{c} 1\land 3=1 \\ 2\land 3=1 \\ 3\land 3=3 \\ 5\land 3=1 \\ 6\land 3=3 \\ 20\land 3=1 \\ 15\land 3=3 \\ 30\land 3=3 \\ \end{array} \\ \end{array} \end{equation*}
    For \(a=5\text{,}\) a similar verification can be performed.
  2. \(6 = 2 \lor 3\text{,}\) \(10 = 2 \lor 5\text{,}\) \(15 = 3 \lor 5\text{,}\) and \(30 = 2 \lor 3 \lor 5\text{.}\)
13.4.3.
Answer.
If \(B = D_{30}\textrm{ }\) 30 then \(A = \{2, 3, 5\}\) and \(D_{30}\) is isomorphic to \(\mathcal{P}(A)\text{,}\) where \(\begin{array}{cc} 1\leftrightarrow \emptyset \textrm{ } & 5\leftrightarrow \{5\} \\ 2\leftrightarrow \{2\}\textrm{ } & 10\leftrightarrow \{2,5\} \\ 3\leftrightarrow \{3\}\textrm{ } & 15\leftrightarrow \{3,5\} \\ 6\leftrightarrow \{2,3\}\textrm{ } & 30\leftrightarrow \{2,3,5\} \\ \end{array}\) and \(\begin{array}{c} \textrm{ Join} \leftrightarrow \textrm{ Union} \\ \textrm{ Meet}\leftrightarrow \textrm{ Intersection} \\ \textrm{ Complement}\leftrightarrow \textrm{ Set} \textrm{ Complement} \\ \end{array}\)
13.4.5.
Hint.
Assume that \([B; \lor , \land, - ]\) is a Boolean algebra of order 3 where \(B = \{0, x, 1\}\) and show that this cannot happen by investigating the possibilities for its operation tables.
Answer.
Assume that \(x \neq 0 \textrm{ or } 1\) is the third element of a Boolean algebra. Then there is only one possible set of tables for join and meet, all following from required properties of the Boolean algebra.
\begin{equation*} \begin{array}{lr} \begin{array}{c|c} \lor & \begin{array}{ccc} 0 & x & 1 \\ \end{array} \\ \hline \begin{array}{c} 0 \\ x \\ 1 \\ \end{array} & \begin{array}{ccc} 0 & x & 1 \\ x & x & 1 \\ 1 & 1 & 1 \\ \end{array} \\ \end{array} & \begin{array}{c|c} \land & \begin{array}{ccc} 0 & x & 1 \\ \end{array} \\ \hline \begin{array}{c} 0 \\ x \\ 1 \\ \end{array} & \begin{array}{ccc} 0 & 0 & 0 \\ 0 & x & x \\ 0 & x & 1 \\ \end{array} \\ \end{array} \end{array} \end{equation*}
Next, to find the complement of \(x\) we want \(y\) such that \(x \land y = 0\) and \(x \lor y = 1\text{.}\) No element satisfies both conditions; hence the lattice is not complemented and cannot be a Boolean algebra. The lack of a complement can also be seen from the ordering diagram from which \(\land\) and \(\lor\) must be derived.
13.4.7.
Answer.
Let \(X\) be any countably infinite set, such as the integers. A subset of \(X\) is cofinite if it is finite or its complement is finite. The set of all cofinite subsets of \(X\) is:
  1. Countably infinite - this might not be obvious, but here is a hint. Assume \(X=\left\{x_0,x_1,x_2,\ldots \right\}\text{.}\) For each finite subset \(A\) of \(X\text{,}\) map that set to the integer \(\sum _{i=0}^{\infty } \chi _A \left(x_i\right)2^i\) You can do a similar thing to sets that have a finite complement, but map them to negative integers. Only one minor adjustment needs to be made to accommodate both the empty set and \(X\text{.}\)
  2. Closed under union
  3. Closed under intersection, and
  4. Closed under complementation.
Therefore, if \(B =\{A \subseteq X : A \textrm{ is cofinite}\}\text{,}\) then \(B\) is a countable Boolean algebra under the usual set operations.
13.4.8.
Hint.
“Copy” the corresponding proof for groups in Section 11.6.

13.5 Finite Boolean Algebras as \(n\)-tuples of 0’s and 1’s

Exercises

13.5.1.
Answer.
  1. \begin{equation*} \begin{array}{lc} \begin{array}{c|cccc} \lor & (0,0) & (0,1) & (1,0) & (1,1) \\ \hline (0,0) & (0,0) & (0,1) & (1,0) & (1,1) \\ (0,1) &(0,1) & (0,1) & (1,1) & (1,1) \\ (1,0) & (1,0) & (1,1) & (1,0) & (1,1) \\ (1,1) & (1,1) & (1,1) & (1,1) & (1,1) \\ \end{array} &\\ \begin{array}{c|cccc} \land & (0,0) & (0,1) & (1,0) & (1,1) \\ \hline (0,0) &(0,0) & (0,0) & (0,0) & (0,0) \\ (0,1) &(0,0) & (0,1) & (0,0) & (0,1) \\ (1,0) &(0,0) & (0,0) & (1,0) & (1,0) \\ (1,1) &(0,0) & (0,1) & (1,0) & (1,1) \\ \end{array} & \begin{array}{c|c} u & \overset{\pmb{\_}}{u} \\ \hline (0,0) & (1,1) \\ (0,1) &(1,0) \\ (1,0) &(0,1) \\ (1,1) &(0,0) \\ \end{array} \\ \end{array} \end{equation*}
  2. The graphs are isomorphic.
  3. (0, 1) and (1,0)
13.5.3.
Answer.
  1. \((1, 0, 0, 0)\text{,}\) \((0, 1, 0, 0)\text{,}\) \((0, 0, 1, 0)\text{,}\) and \((0, 0, 0, 1)\) are the atoms.
  2. The \(n\)-tuples of bits with exactly one 1.

13.6 Boolean Expressions

Exercises

13.6.1.
Answer.
  1. \(\displaystyle \begin{array}{l} f_1\left(x_1,x_2\right)=0 \\ f_2\left(x_1,x_2\right)=\left(\overline{x_1}\land \overline{x_2}\right) \\ f_3\left(x_1,x_2\right)=\left(\overline{x_1}\land x_2\right) \\ f_4\left(x_1,x_2\right)=\left(x_1\land \overline{x_2}\right) \\ f_5\left(x_1,x_2\right)=\left(x_1\land x_2\right) \\ f_6\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right)=\overline{x_1} \\ f_7\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\overline{x_2} \\ f_8\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(\left(x_1\land x_2\right)\lor \left(\overline{x_1}\land \overline{x_2}\right)\right) \\ f_9\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right) \\ f_{10}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=x_2 \\ f_{11}\left(x_1,x_2\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=x_1 \\ f_{12}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\overline{x_1}\lor \overline{x_2}\right) \\ f_{13}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=\left(\overline{x_1}\lor x_2\right) \\ f_{14}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor \overline{x_2}\right) \\ f_{15}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor x_2\right) \\ f_{16}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=1 \\ \end{array}\)
  2. The truth table for the functions in part (a) are
    \begin{equation*} \begin{array}{llllllllll} x_1 & x_2 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7 & f_8\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \end{array} \end{equation*}
    \begin{equation*} \begin{array}{llllllllll} x_1 & x_2 & f_9 & f_{10} & f_{11} & f_{12} & f_{13} & f_{14} & f_{15} & f_{16} \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ \end{array} \end{equation*}
    1. \(\displaystyle g_1\left(x_1,x_2\right)=f_{15}\left(x_1,x_2\right)\)
    2. \(\displaystyle g_2\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)\)
    3. \(\displaystyle g_3\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)\)
    4. \(\displaystyle g_4\left(x_1,x_2\right)=f_{16}\left(x_1,x_2\right)\)
13.6.3.
Answer.
  1. The number of elements in the domain of \(f\) is \(16=4^2=\left| B\right| ^2\)
  2. With two variables, there are \(4^3 = 256\) different Boolean functions. With three variables, there are \(4^8=65536\) different Boolean functions.
  3. \(\displaystyle f\left(x_1,x_2\right)=\left(1\land \overline{x_1}\land \overline{x_2}\right)\lor \left(1\land \overline{x_1}\land x_2\right)\lor \left(1\land x_1\land \overline{x_2}\right)\lor \left(0\land x_1\land x_2\right)\)
  4. Consider \(f:B^2\to B\text{,}\) defined by \(f(0,0)=0\text{,}\) \(f(0,1)=1\text{,}\) \(f(1,0)=a\text{,}\) \(f(1,1)=a\text{,}\) and \(f(0,a)=b\text{,}\) with the images of all other pairs in \(B^2\) defined arbitrarily. This function is not a Boolean function. If we assume that it is Boolean function then \(f\) can be computed with a Boolean expression \(M\left(x_1,x_2\right)\text{.}\) This expression can be put into minterm normal form: \(M\left(x_1,x_2\right)=\left(c_1\land \overline{x_1}\land \overline{x_2}\right)\lor \left(c_2\land \overline{x_1}\land x_2\right)\lor \left(c_3\land x_1\land \overline{x_2}\right)\lor \left(c_4\land x_1\land x_2\right)\)
    \begin{equation*} \begin{array}{c} f(0,0)=0 \Rightarrow M(0,0)=0 \Rightarrow c_1= 0\\ f(0,1)=1 \Rightarrow M(0,0)=1 \Rightarrow c_2= 1\\ f(1,0)=a \Rightarrow M(0,0)=a \Rightarrow c_3= a\\ f(1,1)=a \Rightarrow M(0,0)=a \Rightarrow c_4= a\\ \end{array} \end{equation*}
    Therefore, \(M\left(x_1,x_2\right)=\left(\overline{x_1}\land x_2\right)\lor \left(a\land x_1\land \overline{x_2}\right)\lor \left(a\land x_1\land x_2\right)\) and so, using this formula, \(M(0,a)=\left(\bar{0}\land a\right)\lor \left(a\land 0\land \bar{a}\right)\lor (a\land 0\land a)=a\) This contradicts \(f(0,a)=b\text{,}\) and so \(f\) is not a Boolean function.

13.7 A Brief Introduction to Switching Theory and Logic Design

Exercises

13.7.1.
Answer.
  1. Associative, commutative, and idempotent laws.
  2. Distributive law.
  3. Idempotent and complement laws.
  4. Null and identity laws
  5. Distributive law.
  6. Null and identity laws.
13.7.2.
Answer.
\begin{equation*} (x_1\cdot \overline{x_2})+(x_1\cdot x_2)+(\overline{x_1} \cdot x_2). \end{equation*}
13.7.3.
Answer.
A simpler boolean expression for the function is \(\overline{x_2} \cdot (x_1 + x_3)\text{.}\)
Figure for exercise 3
Figure 13.7.20. An even simpler circuit

14 Monoids and Automata
14.1 Monoids

Exercises

14.1.1.
Answer.
  1. \(S_1\) is not a submonoid since the identity of \(\left[\mathbb{Z}_8; \times_8\right]\text{,}\) which is 1, is not in \(S_1\text{.}\) \(S_2\) is a submonoid since \(1 \in S_2\) and \(S_2\) is closed under multiplication; that is, for all \(a, b \in S_2\text{,}\) \(a \times_8 b\) is in \(S_2\text{.}\)
  2. The identity of \(\mathbb{N}^{\mathbb{N}}\) is the identity function \(i:\mathbb{N}\to \mathbb{N}\) defined by \(i(a) = a\text{,}\) \(\forall a\in \mathbb{N}\text{.}\) If \(a \in \mathbb{N}\text{,}\) \(i(a) = a \leq a\text{,}\) thus the identity of \(\mathbb{N}^{\mathbb{N}}\) is in \(S_1\text{.}\) However, the image of 1 under any function in \(S_2\) is 2, and thus the identity of \(\mathbb{N}^{\mathbb{N}}\) is not in \(S_2\text{,}\) so \(S_2\) is not a submonoid. The composition of any two functions in \(S_1\text{,}\) \(f\) and \(g\text{,}\) will be a function in \(S_1\text{:}\)
    \begin{equation*} \begin{split} (f\circ g)(n) & = f(g(n)) \leq g(n)\textrm{ since } f \textrm{ is in } S_1\\ & \leq n\textrm{ since } g \textrm{ is in } S_1 \Rightarrow f \circ g \in S_1 \end{split} \end{equation*}
    and the two conditions of a submonoid are satisfied and \(S_1\) is a submonoid of \(\mathbb{N}^{\mathbb{N}}\text{.}\)
  3. The first set is a submonoid, but the second is not since the null set has a non-finite complement.
14.1.3.
Answer.
The set of \(n \times n\) real matrices is a monoid under matrix multiplication. This follows from the laws of matrix algebra in Chapter 5. To prove that the set of stochastic matrices is a monoid over matrix multiplication, we need only show that the identity matrix is stochastic (this is obvious) and that the set of stochastic matrices is closed under matrix multiplication. Let \(A\) and \(B\) be \(n \times n\) stochastic matrices.
\begin{equation*} (AB)_{i j}= \sum _{k=1}^n a_{i k} b_{k j} \end{equation*}
The sum of the \(j^{\textrm{th}}\) column is
\begin{equation*} \begin{split} \sum_{j=1}^n (AB)_{i j} & =\sum_{k=1}^n a_{1 k} b_{k j}+\sum_{k=1}^n a_{1k} b_{k j}+\cdots +\sum_{k=1}^n a_{n k} b_{k j}\\ &=\sum_{k=1}^n \left(a_{1 k} b_{k j}+a_{1k} b_{k j}+\cdots +a_{n k} b_{k j}\right)\\ &=\sum _{k=1}^n b_{k j}\left(a_{1 k} +a_{1k}+\cdots +a_{n k} \right)\\ &= \sum _{k=1}^n b_{k j} \quad\textrm{ since } A \textrm{ is stochastic}\\ & = 1 \quad\textrm{ since } B \textrm{ is stochastic}\\ \end{split} \end{equation*}
14.1.5.
Answer.
Let \(f, g, h \in M\text{,}\) and \(a \in B\text{.}\)
\begin{equation*} \begin{split} ((f*g)*h)(a) & = (f*g)(a) \land h(a)\\ & = (f(a)\land g(a))\land h(a)\\ & = f(a) \land ( g(a) \land h(a))\\ & = f(a) \land (g * h)(a)\\ & = (f * (g * h))(a)\\ \end{split} \end{equation*}
Therefore \((f * g) * h =f * (g * h)\) and \(*\) is associative.
The identity for \(*\) is the function \(u \in M\) where \(u(a) = 1\) = the “one” of \(B\text{.}\) If \(a \in B\text{,}\) \((f*u)(a) =f(a)\land u(a) = f(a)\land 1 = f(a)\text{.}\) Therefore \(f * u = f\text{.}\) Similarly, \(u * f =f\text{.}\)
There are \(2^2= 4\) functions in \(M\) for \(B = B _2\text{.}\) These four functions are named in the text. See Figure 14.1.4. The table for \(*\) is
\begin{equation*} \begin{array}{c|cccc} * & z & i & t & u\\ \hline z &z & z & z & z \\ i &z & i & z & i \\ t &z & z & t & t \\ u &z & i & t & u \\ \end{array} \end{equation*}

14.2 Free Monoids and Languages

Exercises

14.2.1.
Answer.
  1. For a character set of 350 symbols, the number of bits needed for each character is the smallest \(n\) such that \(2^n\) is greater than or equal to 350. Since \(2^9= 512 > 350 > 2^8\text{,}\) 9 bits are needed,
  2. \(2^{12}=4096 >3500> 2^{11}\text{;}\) therefore, 12 bits are needed.
14.2.3.
Answer.
This grammar defines the set of all strings over \(B\) for which each string is a palindrome (same string if read forward or backward).
14.2.5.
Answer.
  1. Terminal symbols: The null string, 0, and 1. Nonterminal symbols: \(S\text{,}\) \(E\text{.}\) Starting symbol: \(S\text{.}\) Production rules: \(S\to 00S\text{,}\) \(S\to 01S\text{,}\) \(S\to 10S\text{,}\) \(S\to 11S\text{,}\) \(S\to E\text{,}\) \(E\to 0\text{,}\) \(E\to 1\) This is a regular grammar.
  2. Terminal symbols: The null string, 0, and 1. Nonterminal symbols: \(S\text{,}\) \(A\text{,}\) \(B\text{,}\) \(C\) Starting symbol: \(S\) Production rules: \(S \to 0A\text{,}\) \(S \to 1A\text{,}\) \(S \to \lambda\) , \(A \to 0B\text{,}\) \(A \to 1B\text{,}\) \(A \to \lambda\text{,}\) \(B \to 0C\text{,}\) \(B \to 1C\text{,}\) \(B \to A\text{,}\) \(C \to 0\text{,}\) \(C \to 1\text{,}\) \(C \to \lambda\) This is a regular grammar.
  3. See Exercise 3. This language is not regular.
14.2.7.
Answer.
If \(s\) is in \(A^*\) and \(L\) is recursive, we can answer the question “Is s in \(L^c\text{?}\)” by negating the answer to “Is \(s\) in \(L\text{?}\)”
14.2.9.
Answer.
  1. List the elements of each set \(X_i\) in a sequence \(x_{i 1}\text{,}\) \(x_{i 2}\text{,}\) \(x_{i 3}\ldots\) . Then draw arrows as shown below and list the elements of the union in order established by this pattern: \(x_{11}\text{,}\) \(x_{21}\text{,}\) \(x_{12}\text{,}\) \(x_{13}\text{,}\) \(x_{22}\text{,}\) \(x_{31}\text{,}\) \(x_{41}\text{,}\) \(x_{32}\text{,}\) \(x_{23}\text{,}\) \(x_{14}\text{,}\) \(x_{15}\ldots \text{,}\)
  2. Each of the sets \(A^1\) , \(A^2\) , \(A^3, \ldots\text{,}\) are countable and \(A^*\) is the union of these sets; hence \(A^*\) is countable.
Exercise 9
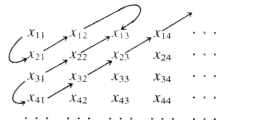
Figure 14.2.23. Exercise 9

14.3 Automata, Finite-State Machines

Exercises

14.3.1.
Answer.
\begin{equation*} \begin{array}{cccc} x & s & Z(x,s) & t(x,s) \\ \textrm{ Deposit} 25\not{c} & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Select} \\ \textrm{ Deposit} 25\not{c} & \textrm{ Select} & \textrm{ Return} 25\not{c} & \textrm{ Select} \\ \textrm{ Press} S & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\ \textrm{ Press} S & \textrm{ Select} & \textrm{ Dispense} S & \textrm{ Locked} \\ \textrm{ Press} P & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\ \textrm{ Press} P & \textrm{ Select} & \textrm{ Dispense} P & \textrm{ Locked} \\ \textrm{ Press} B & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\ \textrm{ Press} B & \textrm{ Select} & \textrm{ Dispense} B & \textrm{ Locked} \\ \end{array} \end{equation*}
Vending Machine Transitions
Figure 14.3.11. Vending Machine Transitions
14.3.3.
Answer.
\(\{000, 011, 101, 110, 111\}\)
14.3.5.
Answer.
    • Input: 10110, Output: 11011 \(\Rightarrow\) 10110 is in position 27
    • Input: 00100, Output: 00111 \(\Rightarrow\) 00100 is in position 7
    • Input:11111, Output: 10101 \(\Rightarrow\) 11111 is in position 21
  2. Let \(x=x_1x_2\ldots x_n\) and recall that for \(n\geq 1\text{,}\) \(G_{n+1}=\left( \begin{array}{c} 0G_n \\ 1G_n^r \\ \end{array} \right)\text{,}\) where \(G_n^r\) is the reverse of \(G_n\text{.}\) To prove that the Gray Code Decoder always works, let \(p(n)\) be the proposition “Starting in Copy state, \(x\)’s output is the position of \(x\) in \(G_n\text{;}\) and starting in Complement state, \(x\)’s output is the position of \(x\) in \(G_n^r\text{.}\)” That p(1) is true is easy to verify for both possible values of \(x\text{,}\) 0 and 1. Now assume that for some \(n\geq 1\text{,}\) \(p(n)\) is true and consider \(x=x_1x_2\ldots x_nx_{n+1}\text{.}\)
    If \(x_1=0\text{,}\) \(x\)’s output is a zero followed by the output for \(\left(x_2\ldots x_nx_{n+1}\right)\) starting in Copy state. By the induction hypothesis, this is zero followed by the position of \(\left(x_2 \ldots x_n x_{n+1}\right)\) in \(G_n\text{,}\) which is the position of \(x\) in \(G_{n+1}\text{,}\) by the definition of \(G\text{.}\)
    If \(x_1=1\text{,}\) \(x\)’s output is a one followed by the output for \(\left(x_2\ldots x_nx_{n+1}\right)\) starting in Complement state. By the induction hypothesis, this is one followed by the position of \(\left(x_2\ldots x_nx_{n+1}\right)\) in \(G_n^r\text{,}\) which is the position of \(x\) in \(G_{n+1}\text{,}\) by the definition of \(G\text{.}\) \(\square\)

14.4 The Monoid of a Finite-State Machine

Exercises

14.4.1.
Hint.
Where the output echoes the current state, the output can be ignored.
Answer.
  1. \(\begin{array}{c|cccccc} \textrm{ Input String} & a & b & c & aa & ab & ac \\ \hline 1 & (a,1) & (a,2) & (c,3) & (a,1) & (a,2) & (c,3) \\ 2 & (a,2) & (a,1) & (c,3) & (a,2) & (a,1) & (c,3) \\ 3 & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) \\ \end{array}\) \(\begin{array}{c|cccccc} \textrm{ Input String} & ba & bb & bc & ca & cb & cc \\ \hline 1 & (a,2) & (a,1) & (c,3) & (c,3) & (c,3) & (c,3) \\ 2 & (a,1) & (a,2) & (c,3) & (c,3) & (c,3) & (c,3) \\ 3 & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) \\ \end{array}\)
    We can see that \(T_aT_a= T_{\textrm{ \textit{aa}}}=T_a\text{,}\) \(T_aT_b= T_{\textrm{ \textit{ab}}}= T_b\text{,}\) etc. Therefore, we have the following monoid:
    \begin{equation*} \begin{array}{c|c} & \begin{array}{ccc} T_{a} & T_b & T_b \\ \end{array} \\ \hline \begin{array}{c} T_a \\ T_b \\ T_c \\ \end{array} & \begin{array}{ccc} T_a & T_b & T_c \\ T_b & T_a & T_c \\ T_c & T_c & T_c \\ \end{array} \\ \end{array} \end{equation*}
    Notice that \(T_a\) is the identity of this monoid.
  2. \(\begin{array}{c|cccccc} \textrm{Input String} & 1 & 2 & 11 & 12 & 21 & 22 \\ \hline A & C & B & A & D & D & A \\ B & D & A & B & C & C & B \\ C & A & D & C & B & B & C \\ D & B & C & D & A & A & D \\ \end{array}\)
    \(\begin{array}{c|cccccccc} \textrm{Input String} &111 & 112 & 121 & 122 & 211 & 212 & 221 & 222 \\ \hline A & C & B & B & C & B & C & C & B \\ B & D & A & A & D & A & D & D & A \\ C & B & C & C & B & C & B & B & C \\ D & B & C & C & B & C & B & B & C \\ \end{array}\)
    We have the following monoid:
    \begin{equation*} \begin{array}{c|c} & \begin{array}{cccc} T_1 & T_2 & T_{11} & T_{12} \\ \end{array} \\ \hline \begin{array}{c} T_1 \\ T_2 \\ T_{11} \\ T_{12} \\ \end{array} & \begin{array}{cccc} T_{11} & T_{12} & T_1 & T_2 \\ T_b & T_{11} & T_2 & T_1 \\ T_1 & T_2 & T_{11} & T_{12} \\ T_2 & T_1 & T_{12} & T_{11} \\ \end{array} \\ \end{array} \end{equation*}
    Notice that \(T_{11}\) is the identity of this monoid.
14.4.3.
Answer.
Yes, just consider the unit time delay machine of Figure 14.4.4. Its monoid is described by the table at the end of Section 14.4 where the \(T_{\lambda }\) row and \(T_{\lambda }\) column are omitted. Next consider the machine in Figure 14.5.7. The monoid of this machine is:
\begin{equation*} \begin{array}{c|ccccccc} & T_{\lambda } & T_0 & T_1 & T_{00} & T_{01} & T_{10} & T_{11} \\ \hline T_{\lambda } & T_{\lambda } & T_0 & T_1 & T_{00} & T_{01} & T_{10} & T_{11} \\ \hline T_0 & T_0 & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\ T_1 & T_1 & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\ T_{00} & T_{00} & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\ T_{01} & T_{01} & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\ T_{10} & T_{10} & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\ T_{11} & T_{11} & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\ \end{array} \end{equation*}
Hence both of these machines have the same monoid, however, their transition diagrams are nonisomorphic since the first has two vertices and the second has seven.

14.5 The Machine of a Monoid

Exercises

14.5.1.
Answer.
solution to 14.5.1a
Figure 14.5.8. (a)
solution to 14.5.1b
Figure 14.5.9. (b)

15 Group Theory and Applications
15.1 Cyclic Groups

Exercises

15.1.1.
Answer.
The only other generator is \(-1\text{.}\)
15.1.3.
Answer.
If \(\lvert G \rvert = m\text{,}\) \(m>2\text{,}\) and \(G = \langle a \rangle\text{,}\) then \(a\text{,}\) \(a^2,\ldots\text{,}\) \(a^{m-1}\) , \(a^m=e\) are distinct elements of \(G\text{.}\) Furthermore, \(a^{-1}= a^{m-1}\neq a\text{,}\) If \(1 \leq k \leq m\text{,}\) \(a^{-1}\) generates \(a^k\text{:}\)
\begin{equation*} \begin{split} \left(a^{-1}\right)^{m-k} &= \left(a^{m-1}\right)^{m-k}\\ & = a^{m^2-m-m k + k}\\ & =\left(a^m\right)^{m-k-1}*a^k\\ &= e*a^k=a^k\\ \end{split} \end{equation*}
Similarly, if \(G\) is infinite and \(G = \langle a\rangle\text{,}\) then \(a^{-1}\) generates \(G\text{.}\)
15.1.5.
Answer.
  1. No. Assume that \(q \in \mathbb{Q}\) generates \(\mathbb{Q}\text{.}\) Then \(\langle q\rangle = \{n q : n \in \mathbb{Z}\}\text{.}\) But this gives us at most integer multiples of \(q\text{,}\) not every element in \(\mathbb{Q}\text{.}\)
  2. No. Similar reasoning to part a.
  3. Yes. 6 is a generator of \(6\mathbb{Z}\text{.}\)
  4. No.
  5. Yes, \((1,1, 1)\) is a generator of the group.
15.1.7.
Answer.
Theorem 15.1.13 implies that \(a\) generates \(\mathbb{Z}_n\) if and only if the greatest common divisor of \(n\) and \(a\) is 1. Therefore the list of generators of \(\mathbb{Z}_n\) are the integers in \(\mathbb{Z}_n\) that are relatively prime to \(n\text{.}\) The generators of \(\mathbb{Z}_{25}\) are all of the nonzero elements except 5, 10, 15, and 20. The generators of \(\mathbb{Z}_{256}\) are the odd integers in \(\mathbb{Z}_{256}\) since 256 is \(2^8\text{.}\)
15.1.9.
Answer.
  1. \(\theta :\mathbb{Z}_{77} \to \mathbb{Z}_7 \times \mathbb{Z}_{11}\) maps the given integers as follows:
    \begin{equation*} \begin{array}{ccc} 21 & \to & (0,10) \\ 5 & \to & (5,5) \\ 7 & \to & (0,7) \\ 15 & \to & \underline{(1,4)} \\ \textrm{ sum}=48 & \leftarrow & (6,4)=\textrm{ sum} \\ \end{array} \end{equation*}
    The final sum, 48, is obtained by using the facts that \(\theta ^{-1}(1,0) =22\) and \(\theta ^{-1}(0,1)=56\)
    \begin{equation*} \begin{split} \theta^{-1}(6,4)= 6 \times_{77}\theta ^{-1}(1,0) + 4 \times_{77}\theta^{-1}(0,1)\\ & =6\times_{77}22 +_{77} 4\times_{77} 56\\ & =55 +_{77}70\\ & =48\\ \end{split}\text{.} \end{equation*}
  2. Using the same isomorphism:
    \begin{equation*} \begin{array}{ccc} 25 & \to & (4,3) \\ 26 & \to & (5,4) \\ 40 & \to & (5,7) \\ & & \textrm{ sum}=(0,3) \\ \end{array} \end{equation*}
    \begin{equation*} \begin{split} theta ^{-1}(0,3) &= 3 \times_{77}\theta ^{-1}(0,1)\\ & = 3\times_{77} 56\\ & =14\\ \end{split}\text{.} \end{equation*}
    The actual sum is 91. Our result is incorrect, since 91 is not in \(\mathbb{Z}_{77}\text{.}\) Notice that 91 and 14 differ by 77. Any error that we get using this technique will be a multiple of 77.

15.2 Cosets and Factor Groups

Exercises

15.2.1.
Answer.
An example of a valid correct answer: Call the subsets \(A\) and \(B\) respectively. If we choose \(0 \in A\) and \(5 \in B\) we get \(0 +_{10} 5 =5 \in B\text{.}\) On the other hand, if we choose \(3 \in A\) and \(8 \in B\text{,}\) we get \(3 +_{10} 8 = 1 \in A\text{.}\) Therefore, the induced operation is not well defined on \(\{A,B\}\text{.}\)
15.2.3.
Answer.
  1. The four distinct cosets in \(G/H\) are \(H = \{(0, 0), (2, 0)\}\text{,}\) \((1, 0) + H= \{(1,0),(3,0)\}\text{,}\) \((0, 1) + H= \{(0,1),(2,1)\}\text{,}\) and \((1, 1) + H= \{(1,1),(3,1)\}\text{.}\) None of these cosets generates \(G/H\text{;}\) therefore \(G/H\) is not cyclic. Hence \(G/H\) must be isomorphic to \(\mathbb{Z}_2\times \mathbb{Z}_2\text{.}\)
  2. The factor group is isomorphic to \([\mathbb{R}; +]\text{.}\) Each coset of \(\mathbb{R}\) is a line in the complex plane that is parallel to the x-axis: \(\tau :\mathbb{C}/\mathbb{R}\to \mathbb{R}\text{,}\) where \(T(\{a + b i\mid a\in \mathbb{R}\}) = b\) is an isomorphism.
  3. \(\langle 8\rangle = \{0, 4, 8, 12, 16\} \)\(\Rightarrow\) \(\lvert \mathbb{Z}_{20}/\langle 8\rangle \rvert =4\text{.}\) The four cosets are: \(\bar{0}\text{,}\) \(\bar{1}\text{,}\) \(\bar{2}\text{,}\) and \(\bar{3}\text{.}\) 1 generates all four cosets. The factor group is isomorphic to \([\mathbb{Z}_4; +_4]\) because \(\bar{1}\) is a generator.
15.2.5.
Answer.
\begin{equation*} \begin{split} a*H= b*H &\Leftrightarrow a \in b H\\ &\Leftrightarrow a = b * h \textrm{ for some }h \in H\\ &\Leftrightarrow b^{-1}*a = h \textrm{ for some }h \in H\\ & \Leftrightarrow b^{-1}*a \in H\\ \end{split} \end{equation*}

15.3 Permutation Groups
15.3.5 Exercises

15.3.5.1.

Answer.
  1. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \\ \end{array} \right)\)
  2. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 1 & 2 \\ \end{array} \right)\)
  3. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)\)
  4. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)\)
  5. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right)\)
  6. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 1 & 4 & 2 \\ \end{array} \right)\)
  7. \(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)\)

15.3.5.3.

Answer.
\(S_3/A_3\) is a group of order two. The operation on left cosets of \(H=\left\langle f_1\right\rangle\) is not well defined and so a group cannot be formed from left cosets of \(H\text{.}\)

15.3.5.5.

Answer.
\(\mathcal{D}_4 = \left\{i, r, r^2, r^3, f_1, f_2, f_3, f_4\right\}\) Where \(i\) is the identity function, \(r=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{array} \right)\text{,}\) and
\begin{equation*} \begin{array}{cc} f_1 =\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \\ \end{array} \right) & f_2 =\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right) \\ f_3 =\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 2 & 1 & 4 \\ \end{array} \right) & f_4 =\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \\ \end{array} \right) \\ \end{array} \end{equation*}
The operation table for the group is
\begin{equation*} \begin{array}{c|c} \circ & \textrm{ } \begin{array}{cccccccc} i & r & r^2 & r^3 & f_1 & f_2 & f_3 & f_4 \\ \end{array} \\ \hline \begin{array}{c} i \\ r \\ r^2 \\ r^3 \\ f_1 \\ f_2 \\ f_3 \\ f_4 \\ \end{array} & \begin{array}{cccccccc} i & r & r^2 & r^3 & f_1 & f_2 & f_3 & f_4 \\ r & r^2 & r^3 & i & f_4 & f_3 & f_1 & f_2 \\ r^2 & r^3 & i & r & f_2 & f_1 & f_4 & f_3 \\ r^3 & i & r & r^2 & f_3 & f_4 & f_2 & f_1 \\ f_1 & f_3 & f_2 & f_4 & i & r^2 & r & r^3 \\ f_2 & f_4 & f_1 & f_3 & r^2 & i & r^3 & r \\ f_3 & f_2 & f_4 & f_1 & r^3 & r & i & r^2 \\ f_4 & f_1 & f_3 & f_2 & r & r^3 & r^2 & i \\ \end{array} \\ \end{array} \end{equation*}
A lattice diagram of its subgroups is
described in detail following the image
Subgroups of \(\mathcal{D}_4\)
Figure 15.3.30. Subgroups of \(\mathcal{D}_4\)
All proper subgroups are cyclic except \(\left\{i,r^2,f_1,f_2\right\}\)\(\textrm{ }\textrm{ }\)and \(\left\{i,r^2,f_3,f_4\right\}\text{.}\) Each 2-element subgroup is isomorphic to \(\mathbb{Z}_2\) ; \(\left\{i,r,r^2,r^3\right\}\) is isomorphic to \(\mathbb{Z}_4\) ; and \(\left\{i,r^2,f_1,f_2\right\}\)\(\textrm{ }\textrm{ }\)and \(\left\{i,r^2,f_3,f_4\right\}\) are isomorphic to \(\mathbb{Z}_2\times \mathbb{Z}_2\text{.}\)

15.3.5.7.

Answer.
One solution is to cite Exercise 3 at the end of Section 11.3. It can be directly applied to this problem. An induction proof of the problem at hand would be almost identical to the proof of the more general statement. \(\left(t_1t_2\cdots t_r\right){}^{-1}= t_r{}^{-1}\cdots t_2{}^{-1}t_1{}^{-1}\quad\textrm{ by Exercise 3 of Section 11.3}\\ \\ \quad \quad = t_r\cdots t_2t_1\textrm{ }\textrm{ since} \textrm{ each} \textrm{ transposition} \textrm{ inverts} \textrm{ itself}.\textrm{ }\blacksquare\)

15.3.5.9.

Answer.
Part I: That \(\lvert S_k \rvert = k!\) follows from the Rule of Products.
Part II: Let \(f\) be the function defined on \(\{1,2,\textrm{ ...}, n\}\) by \(f(1)=2\text{,}\) \(f(2)=3\text{,}\) \(f(3)=1\text{,}\) and \(f(j) =j\) for \(4\leq j\leq n\text{;}\) and let \(g\) be defined by \(g(1) = 1\text{,}\) \(g(2) = 3\text{,}\) \(g(3) = 2\text{,}\) and \(g(j) =j\) for \(4\leq j\leq n\text{.}\) Note that \(f\) and \(g\) are elements of \(S_n\text{.}\) Next, \((f\circ g)(1) = f(g(1)) = f(1) = 2\text{,}\) while \((g \circ f)(1) = g(f(1)) = g(2) = 3\text{,}\) hence \(f\circ g\neq g\circ f\) and \(S_n\) is non-abelian for any \(n \geq 3\text{.}\)

15.3.5.13.

Answer.
  1. Both groups are non-abelian and of order 6; so they must be isomorphic, since only one such group exists up to isomorphism. The function \(\theta:S_3\to R_3\) defined by \(\begin{array}{cc} \theta(i)=I & \theta\left(f_1\right)=F_1 \\ \theta\left(r_1\right)=R_1 & \theta\left(f_2\right)=F_2 \\ \theta\left(r_2\right)=R_2 & \theta\left(f_3\right)=F_3 \\ \end{array}\) is an isomorphism,
  2. Recall that since every function is a relation, it is natural to translate functions to Boolean matrices. Suppose that \(f\in S_n\text{.}\) We will define its image, \(\theta(f)\text{,}\) by
    \begin{equation*} \theta(f)_{kj}=1\textrm{ }\Leftrightarrow \textrm{ }f(j)=k \end{equation*}
    That \(\theta\) is a bijection follows from the existence of \(\theta^{-1}\text{.}\) If \(A\) is a rook matrix,
    \begin{equation*} \begin{split} \theta^{-1}(A)(j)=k &\Leftrightarrow \textrm{ }\textrm{The } 1 \textrm{ in} \textrm{ column } j \textrm{ of } A \textrm{ appears} \textrm{ in} \textrm{ row } k \\ &\Leftrightarrow A_{kj}=1 \end{split} \end{equation*}
    For \(f,g\in S_n\text{,}\)
    \begin{equation*} \begin{split} \theta(f\circ g)_{kj}= 1 & \Leftrightarrow \textrm{ }(f \circ g)(j)=k\\ & \Leftrightarrow \exists l\textrm{ such that }g(j)=l \textrm{ and } f(l)=k\\ & \Leftrightarrow \exists l\textrm{ such that } \theta(g)_{lj}=1\textrm{ and }\textrm{}\theta(f)_{kl}=1\\ & \Leftrightarrow (\theta(f)\theta(g))_{kj}=1 \end{split} \end{equation*}
    Therefore, \(\theta\) is an isomorphism.

15.4 Normal Subgroups and Group Homomorphisms
15.4.3 Exercises

15.4.3.1.

Answer.
  1. Yes, the kernel is \(\{1, -1\}\)
  2. No, since \(\theta _2\left(2 +_{5} 4\right)= \theta_2(1)=1\text{,}\) but \(\theta _2(2)+_2\theta_{2} (4)=0+_{2}0 =0\)
    A follow-up might be to ask what happens if 5 is replaced with some other positive integer in this part.
  3. Yes, the kernel is \(\{(a, -a)| a \in \mathbb{R}\}\)
  4. No. A counterexample, among many, would be to consider the two transpositions \(t_1=(1,3)\) and \(t_2=(1,2)\text{.}\) Compare \(\theta_4(t_1 \circ t_2)\) and \(\theta_4(t_1) \circ \theta_4(t_2)\text{.}\)

15.4.3.3.

Answer.
\(\langle r\rangle =\left\{i,r,r^2,r^3\right\}\) is a normal subgroup of \(D_4\text{.}\) To see you could use the table given in the solution of Exercise 15.3.5.5 of Section 15.3 and verify that \(a^{-1}h a \in \langle r\rangle\) for all \(a\in D_4\) and \(h\in \langle r\rangle\text{.}\) A more efficient approach is to prove the general theorem that if \(H\) is a subgroup \(G\) with exactly two distinct left cosets, than \(H\) is normal. \(\left\langle f_1\right\rangle\) is not a normal subgroup of \(D_4\text{.}\) \(\left\langle f_1\right\rangle =\left\{i,f_1\right\}\) and if we choose \(a = r\) and \(h=f_1\) then \(a^{-1}h a= r^3f_1r=f_2\notin \left\langle f_1\right\rangle\)

15.4.3.5.

Answer.
\((\beta \circ \alpha )\left(a_1,a_2,a_3\right) = 0\) and so \(\beta \circ \alpha\) is the trivial homomorphism, but a homomorphism nevertheless.

15.4.3.7.

Answer.
Let \(x, y \in G\text{.}\)
\begin{equation*} \begin{split} q(x * y) &= (x * y)^2\\ & = x*y*x*y \\ & = x*x*y*y \quad\textrm{ since } G \textrm{ is abelian}\\ & =x^2*y^2 \\ &= q(x)*q(y) \end{split} \end{equation*}
Hence, \(q\) is a homomorphism. In order for \(q\) to be an isomorphism, it must be the case that no element other than the identity is its own inverse.
\begin{equation*} \begin{split} x \in \textrm{Ker}(q) & \Leftrightarrow q (x) = e \\ & \Leftrightarrow x * x =e \\ & \Leftrightarrow x^{-1}= x\\ \end{split} \end{equation*}

15.4.3.9.

Answer.
Proof: Recall that the inverse image of \(H'\) under \(\theta\) is \(\theta ^{-1}(H')=\{g\in G | \theta (g)\in H'\}\text{.}\)
Closure: Let \(g_1, g_2\in \theta ^{-1}(H')\text{,}\) then \(\theta \left(g_1\right),\theta \left(g_2\right)\in H'\text{.}\) Since \(H'\) is a subgroup of \(G'\text{,}\)
\begin{equation*} \theta\left(g_1\right)\diamond \theta\left(g_2\right)=\theta\left(g_1*g_2\right)\in H' \Rightarrow g_1*g_2\in \theta^{-1}(H') \end{equation*}
Identity: By Theorem 15.4.14(a), \(e \in \theta ^{-1}(H')\text{.}\)
Inverse: Let \(a\in \theta ^{-1}(H')\) . Then \(\theta (a)\in H'\) and by Theorem 15.4.14(b), \(\theta (a)^{-1}= \theta \left(a^{-1}\right)\in H'\) and so \(a^{-1}\in \theta ^{-1}(H')\text{.}\)

15.5 Coding Theory, Linear Codes
15.5.4 Exercises

15.5.4.1.

Answer.
  1. Error detected, since an odd number of 1’s was received; ask for retransmission.
  2. No error detected; accept this block.
  3. No error detected; accept this block.

15.5.4.3.

Answer.
  1. Syndrome = \((1,0,1)\text{.}\) Corrected coded message is \((1,1,0,0,1,1)\) and original message was \((1, 1, 0)\text{.}\)
  2. Syndrome = \((1,1,0)\text{.}\) Corrected coded message is \((0,0,1,0,1,1)\) and original message was \((0, 0, 1)\text{.}\)
  3. Syndrome = \((0,0,0)\text{.}\) No error, coded message is \((0,1,1,1,1,0)\) and original message was \((0, 1, 1)\text{.}\)
  4. Syndrome = \((1, 1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)
  5. Syndrome = \((1,1,1)\text{.}\) This syndrome occurs only if two bits have been switched. No reliable correction is possible.
  6. Syndrome = \((0,1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)

15.5.4.5.

Answer.
  1. Blocks of two bits are encoded into code words of length 4.
  2. The code words are 0000, 1010, 0111 and 1101.
  3. Since the first two code words have a Hamming distance of 2, not all single bit errors can be corrected. For example, if 0000 is transmitted and the first bit is switch, then 1000 is received and we can’t tell for sure whether this came from 0000 or 1010. To see what can be corrected, we note that \(a_1 a_2\) is encoded to \(a_1 a_2 (a_1 +_2 a_2) a_2\) and so if \(b_1 b_2 b_3 b_4\) is recieved and no error has occurred,
    \begin{gather*} b_1 +_2 b_2 +_2 b_3 =0\\ b_2 +_2 b_4 =0 \end{gather*}
    We can extract the parity check matrix from this set of equations. It is
    \begin{equation*} \begin{pmatrix} 1 & 0 \\ 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{pmatrix} \end{equation*}
    The rows of this matrix correspond with the syndromes for errors in bits 1 through 4, which are all nonzero, so we can detect any single bit error. Notice that the syndromes for bits 1 and 3 are identical. This reflects the fact that errors in these bits can’t be corrected. However, the syndromes for bits 2 and 4 are unique and so we can correct them. Therefore the second bit of the original message can be sent with more confidence than the first.

15.5.4.7.

Solution.
Yes, you can correct all single bit errors because the parity check matrix for the expanded code is
\begin{equation*} H = \left(\begin{array}{ccc} 1 & 1 & 0\\ 1 & 0 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{array} \right). \end{equation*}
Since each possible syndrome of single bit errors is unique we can correct any error.

15.5.4.8.

Hint.
There is a parity check equation for each parity bit.

16 An Introduction to Rings and Fields
16.1 Rings, Basic Definitions and Concepts
16.1.6 Exercises

16.1.6.1.

Answer.
All but ring d are commutative. All of the rings have a unity element. The number 1 is the unity for all of the rings except d. The unity for \(M_{2\times 2}(\mathbb{R})\) is the two by two identity matrix. The units are as follows:
  1. \(\displaystyle \{1, -1\}\)
  2. \(\displaystyle \mathbb{C}^*\)
  3. \(\displaystyle \mathbb{Q}^*\)
  4. \(\displaystyle \left\{A \left| A_{11}A_{22}-A_{12}A_{21}\neq 0\right.\right\}\)
  5. \(\displaystyle \{1\}\)

16.1.6.3.

Answer.
  1. Consider commutativity
  2. Solve \(x ^2=3x\) in both rings.

16.1.6.5.

Answer.
  1. We already know that \(3\mathbb{Z}\) is a subgroup of the group \(\mathbb{Z}\text{.}\) We need only show that \(3\mathbb{Z}\) is closed with respect to multiplication. Let \(3m, 3n \in 3\mathbb{Z}\text{.}\) \((3m)(3n) = 3(3m n) \in 3\mathbb{Z}\text{,}\) since \(3 m n \in \mathbb{Z}\text{.}\)
  2. The proper subrings are \(\{0, 2, 4, 6\}\) and \(\{0, 4\}\text{;}\) while \(\{0\}\) and \(\mathbb{Z}_8\) are improper subrings.
  3. The proper subrings are \(\{00, 01\}\text{,}\) \(\{00, 10\}\text{,}\) and \(\{00,11\}\text{:}\) while \(\{00\}\) and \(\mathbb{Z}_2\times \mathbb{Z}_2\) are improper subrings.

16.1.6.7.

Answer.
  1. The left-hand side of the equation factors into the product \((x-2)(x-3)\text{.}\) Since \(\mathbb{Z}\) is an integral domain, \(x = 2\) and \(x =3\) are the only possible solutions.
  2. Over \(\mathbb{Z}_{12}\text{,}\) 2, 3, 6, and 11 are solutions. Although the equation factors into \((x-2)(x-3)\text{,}\) this product can be zero without making \(x\) either 2 or 3. For example. If \(x\) = 6 we get \((6-2)\times _{12}(6-3)=4 \times _{12}3 = 0\text{.}\) Notice that 4 and 3 are zero divisors.

16.1.6.9.

Answer.
Let \(R_1\text{,}\) \(R_2\text{,}\) and \(R_3\) be any rings, then
  1. \(R_1\) is isomorphic to \(R_1\) and so “is isomorphic to” is a reflexive relation on rings.
  2. \(R_1\) is isomorphic to \(R_2\) \(\Rightarrow\) \(R_2\) is isomorphic to \(R_1\text{,}\) and so “is isomorphic to” is a symmetric relation on rings,
  3. \(R_1\) is isomorphic to \(R_2\text{,}\) and \(R_2\) is isomorphic to \(R_3\) implies that \(R_1\) is isomorphic to \(R_3\text{,}\) and so “is isomorphic to” is a transitive relation on rings.
We haven’t proven these properties here, just stated them. The combination of these observations implies that “is isomorphic to” is an equivalence relation on rings.

16.1.6.11.

Answer.
  1. Commutativity is clear from examination of a multiplication table for \(\mathbb{Z}_2\times \mathbb{Z}_3\text{.}\) More generally, we could prove a theorem that the direct product of two or more commutative rings is commutative. \((1, 1)\) is the unity of \(\mathbb{Z}_2\times \mathbb{Z}_3\text{.}\)
  2. \(\displaystyle \{(m, n) | m = 0 \textrm{ or } n = 0, (m, n) \neq (0, 0)\}\)
  3. Another example is \(\mathbb{Z} \times \mathbb{Z}\text{.}\) You never get an integral domain in this situation. By the definition an integral domain \(D\) must contain a “zero” so we always have \((1, 0) \cdot (0, 1) = (0, 0)\) in \(D \times D\text{.}\)

16.1.6.13.

Answer.
  1. \(\displaystyle (a + b)(c + d) = (a + b)c + (a + b)d = a c + b c + a d + b d\)
  2. \begin{equation*} \begin{split} (a + b)(a + b ) &= a a + b a + a b + b b\quad \textrm{ by part a}\\ & = a a + a b + a b + b b\quad \textrm{ since } R \textrm{ is commutative}\\ & =a^2 + 2a b + b^2 \end{split}\text{.} \end{equation*}

16.2 Fields

Exercises

16.2.5.
Answer.
  1. 0 in \(\mathbb{Z}_2\text{,}\) 1 in \(\mathbb{Z}_3\text{,}\) 3 in \(\mathbb{Z}_5\)
  2. 2 in \(\mathbb{Z}_3\text{,}\) 3 in \(\mathbb{Z}_5\)
  3. 2 in \(\mathbb{Z}_5\)
16.2.7.
Answer.
  1. 0 and 1
  2. 1
  3. 1
  4. none

16.3 Polynomial Rings

Exercises

16.3.1.
Answer.
  1. \(f(x) + g(x) = 2 + 2x + x^2\) , \(f(x)\cdot g(x) =1 +2x +2x^2+x^3\)
  2. \(f(x)+g(x)=x^2\text{,}\) \(f(x)\cdot g(x) =1+x^3\)
  3. \(\displaystyle 1 + 3x + 4x ^2 + 3x^3 + x^4\)
  4. \(\displaystyle 1 + x + x^3 + x^4\)
  5. \(\displaystyle x^2+ x^3\)
16.3.3.
Answer.
  1. If \(a, b \in \mathbb{R}\text{,}\) \(a - b\) and \(a b\) are in \(\mathbb{R}\) since \(\mathbb{R}\) is a ring in its own right. Therefore, \(\mathbb{R}\) is a subring of \(\mathbb{R}[x]\text{.}\) The proofs of parts b and c are similar.
16.3.5.
Answer.
  1. Reducible, \((x+1)\left(x^2+ x+1\right)\)
  2. Reducible, \(x\left(x^2+x+1\right)\)
  3. Irreducible. If you could factor this polynomial, one factor would be either \(x\) or \(x + 1\text{,}\) which would give you a root of 0 or 1, respectively. By substitution of 0 and 1 into this polynomial, it clearly has no roots.
  4. Reducible, \((x+1)^{4 }\)
16.3.7.
Answer.
We illustrate this property of polynomials by showing that it is not true for a nonprime polynomial in \(\mathbb{Z}_2[x]\text{.}\) Suppose that \(p(x) = x^2+ 1\text{,}\) which can be reduced to \((x+1)^2\) , \(a(x) = x^2 + x\text{,}\) and \(b(x) = x^3 + x^2\text{.}\) Since \(a(x)b(x) =x^5+x^3= x^3\left(x^2+1\right)\text{,}\) \(p(x)|a(x)b(x)\text{.}\) However, \(p(x)\) is not a factor of either \(a(x)\) or \(b(x)\text{.}\)
16.3.9.
Answer.
The only possible proper factors of \(x^2- 3\) are \(\left(x - \sqrt{3}\right)\) and \(\left(x+\sqrt{3}\right)\text{,}\) which are not in \(\mathbb{Q}[x]\) but are in \(\mathbb{R}\)[x].
16.3.11.
Answer.
For \(n \geq 0\text{,}\) let \(S(n)\) be the proposition: For all \(g(x)\neq 0\) and \(f(x)\) with \(\deg f(x) = n\text{,}\) there exist unique polynomials \(q(x)\) and \(r(x)\) such that \(f(x)=g(x)q(x)+r(x)\text{,}\) and either \(r(x)=0\) or \(\deg r(x) < \deg g(x)\text{.}\)
Basis: \(S(0)\) is true, for if \(f(x)\) has degree 0, it is a nonzero constant, \(f(x)=c\neq 0,\) and so either \(f(x) =g(x)\cdot 0 + c\) if \(g(x)\) is not a constant, or \(f(x) = g(x)g(x)^{-1}+0\) if \(g(x)\) is also a constant.
Induction: Assume that for some \(n\geq 0\text{,}\) \(S(k)\) is true for all \(k \leq n\text{,}\) If \(f(x)\) has degree \(n+1\text{,}\) then there are two cases to consider. If \(\deg g(x) > n + 1\text{,}\) \(f(x) = g(x)\cdot 0 + f(x)\text{,}\) and we are done. Otherwise, if \(\deg g(x) =m \leq n + 1\text{,}\) we perform long division as follows, where LDT’s stand for terms of lower degree than \(n+1\text{.}\)
\begin{equation*} \begin{array}{rll} & f_{n+1}\cdot g_m{}^{-1}x^{n+1-m} \\ g_mx^m+ \textrm{ LDT}'s & \overline{\left) f_{n+1}x^{n+1}\right.+ \textrm{ LDT}'s \textrm{ }}& \\ & \underline{\textrm{ }f_{n+1}x^{n+1}+ \textrm{ LDT}'s}\textrm{ }\\& \quad\quad\quad\quad\quad h(x) \\ \end{array} \end{equation*}
Therefore,
\begin{equation*} h(x) = f(x)-\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right) g(x) \Rightarrow \textrm{ }f(x) = \left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right) g(x)+h(x) \end{equation*}
Since \(\deg h(x)\) is less than \(n+1\text{,}\) we can apply the induction hypothesis: \(h(x) = g(x)q(x) + r(x)\) with \(\deg r(x) < \deg g(x)\text{.}\)
Therefore,
\begin{equation*} f(x) = g(x)\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}+ q(x)\right) + r(x) \end{equation*}
with \(\deg r(x) < \deg g(x)\text{.}\) This establishes the existence of a quotient and remainder. The uniqueness of \(q(x)\) and \(r(x)\) as stated in the theorem is proven as follows: if \(f(x)\) is also equal to \(g(x)\bar{q}(x) + \bar{r}(x)\) with deg \(\bar{r}(x) < \deg g(x)\text{,}\) then
\begin{equation*} g(x)q(x) + r(x) = g(x) \bar{q}(x) +\overline{ r}(x) \Rightarrow g(x) \left(\bar{q}(x)-q(x)\right)= r(x)-\bar{r}(x) \end{equation*}
Since \(\deg r(x) - \bar{r}(x) < \deg g(x)\text{,}\) the degree of both sides of the last equation is less than \(\deg g(x)\text{.}\) Therefore, it must be that \(\bar{q}(x) - q(x) = 0\text{,}\) or \(q(x) =\bar{q}(x)\) And so \(r(x) = \bar{r}(x)\text{.}\)

16.4 Field Extensions

Exercises

16.4.1.
Answer.
If \(a_0+ a_1\sqrt{2}\in \mathbb{Q}\left[\sqrt{2}\right]\) is nonzero, then it has a multiplicative inverse:
\begin{equation*} \begin{split} \frac{1}{a_0+ a_1\sqrt{2}} &=\frac{1}{a_0+ a_1\sqrt{2}}\frac{a_0- a_1\sqrt{2}}{a_0- a_1\sqrt{2}}\quad\\ & =\frac{a_0- a_1\sqrt{2}}{a_0{}^2- 2a_1{}^2}\\ & =\frac{a_0}{a_0{}^2- 2a_1{}^2}-\frac{ a_1}{a_0{}^2- 2a_1{}^2}\sqrt{2} \end{split} \end{equation*}
The denominator, \(a_0{}^2- 2a_1{}^2\text{,}\) is nonzero since \(\sqrt{2}\) is irrational. Since \(\frac{a_0}{a_0{}^2- 2a_1{}^2}\) and\(\frac{-a_1}{a_0{}^2- 2a_1{}^2}\) are both rational numbers, \(a_0+ a_1\sqrt{2}\) is a unit of \(\mathbb{Q}\left[\sqrt{2}\right]\text{.}\) The field containing \(\mathbb{Q}\left[\sqrt{2}\right]\) is denoted \(\mathbb{Q}\left(\sqrt{2}\right)\) and so \(\mathbb{Q}\left(\sqrt{2}\right)=\mathbb{Q}\left[\sqrt{2}\right]\)
16.4.3.
Answer.
\(x^4 - 5x^2 +6 = (x^2 - 2)(x^2 - 3)\) has zeros \(\pm \sqrt{2}\) and \(\pm \sqrt{3}\text{.}\)
\(\mathbb{Q}(\sqrt{2}) = \{a + b\sqrt{2} \mid a, b \in \mathbb{Q}\}\) contains the zeros \(\pm \sqrt{2}\) but does not contain \(\pm \sqrt{3}\text{,}\) since neither are expressible in the form \(a + b\sqrt{2}\text{.}\) If we consider the set \(\{c + d\sqrt{3} \mid c,d \in \mathbb{Q}(\sqrt{2})\}\text{,}\) then this field contains \(\pm \sqrt{3}\) as well as \(\pm \sqrt{2}\text{,}\) and is denoted \(\mathbb{Q}(\sqrt{2})(\sqrt{3})= \mathbb{Q}(\sqrt{2}, \sqrt{3})\text{.}\) Taking into account the form of \(c\) and \(d\) in the description above, we can expand to
\begin{equation*} \mathbb{Q}(\sqrt{2},\sqrt{3})= \{b_0 + b_1\sqrt{2} + b_2 \sqrt{3} +b_3\sqrt{6} \mid b_i \in \mathbb{Q}\} \end{equation*}
16.4.5.
Answer.
  1. \(f(x) = x^3 + x + 1\) is reducible if and only if it has a factor of the form \(x- a\text{.}\) By Theorem 16.3.14, \(x-a\) is a factor if and only if \(a\) is a zero. Neither 0 nor 1 is a zero of \(f(x)\) over \(\mathbb{Z}_2\text{.}\)
  2. Since \(f(x)\) is irreducible over \(\mathbb{Z}_2\text{,}\) all zeros of \(f(x)\) must lie in an extension field of \(\mathbb{Z}_2\) . Let c be a zero of \(f(x)\text{.}\) \(\mathbb{Z}_2(c)\) can be described several different ways. One way is to note that since \(c \in \mathbb{Z}_2(c)\text{,}\) \(c^n\in \mathbb{Z}_2(c)\) for all n. Therefore, \(\mathbb{Z}_2(c)\) includes 0, \(c\text{,}\) \(c^2\text{,}\) \(c^3, \ldots\text{.}\) But \(c^3 = c + 1\) since \(f(c) = 0\text{.}\) Furthermore, \(c^4 = c^2+ c\text{,}\) \(c^5= c^2+ c +1\text{,}\) \(c^6= c^2+1\text{,}\) and \(c^7=1\text{.}\) Higher powers of \(c\) repeat preceding powers. Therefore,
    \begin{equation*} \begin{split} \mathbb{Z}_2(c)&= \left\{0, 1, c, c^2 , c + 1, c^2 + 1, c^2 + c + 1, c ^2 + c\right\}\\ &= \left\{a_0+ a_1c+a_2c^2 \mid a_i\in \mathbb{Z}_2\right\}\\ \end{split} \end{equation*}
    The three zeros of \(f(x)\) are \(c\text{,}\) \(c^2\) and \(c^2+ c\text{.}\)
    \begin{equation*} f(x) = (x + c)\left(x+ c ^2 \right)\left(x + c^2 + c\right) \end{equation*}
  3. Cite Theorem Theorem 16.2.10, part 3.

16.5 Power Series
16.5.3 Exercises

16.5.3.5.

Answer.
  1. \begin{equation*} \begin{array}{c} b_0= 1\\ b_1=(-1)(2\cdot 1) = -2\\ b_2=(-1)(2\cdot (-2)+4\cdot 1)= 0\\ b_3= (-1)(2\cdot 0 + 4\cdot (-2)+8\cdot 1)=0\\ \end{array} \end{equation*}
    All other terms are zero. Hence, \(f(x)^{-1}= 1-2x\)
  2. \begin{equation*} \begin{split} f(x) &=1+2x + 2^2x^2+ 2^3x^3+ \cdots \\ &=(2x)^0 + (2x)^1 + (2x)^2+ (2x)^3+\cdots \\ &= \frac{1}{1-2x}\\ \end{split} \end{equation*}
    The last step follows from the formula for the sum of a geometric series.

16.5.3.7.

Answer.
  1. \begin{equation*} \begin{split} \left(x^4-x^5\right)^{-1} & =(x^4 (1-x))^{-1}\\ &=x^{-4}\frac{1}{1-x}\\ & =x^{-4}\left(\sum_{k=0}^{\infty } x^k\right)\\ &=\sum_{k=-4}^{\infty} x^k\\ \end{split}\text{.} \end{equation*}
  2. \begin{equation*} \begin{split} \left(x^4-2 x^3+x^2\right)^{-1} & =\left(x^2 \left(x^2-2 x+1\right)\right)^{-1}\\ &=x^{-2}\left(1-2x+x^2\right)^{-1}\\ & =x^{-2}\left(\sum_{k=0}^{\infty } (k+1) x^k\right)\\ &=\sum_{k=-2}^{\infty} (k+2) x^k\\ \end{split}\text{.} \end{equation*}
PrevTopNext