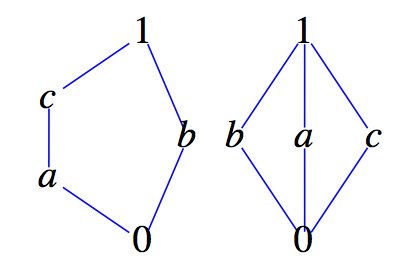
We now give an example of a lattice where the distributive laws do not hold. Let \(L = \{\pmb{0},a,b,c,\pmb{1}\}\text{.}\) We define the partial ordering \(\preceq\) on \(L\) by the set
\begin{equation*}
\{(\pmb{0},\pmb{0}),(\pmb{0},a),(\pmb{0},b),(\pmb{0},c),(\pmb{0},\pmb{1}),(a,a),(a,\pmb{1}),(b,b),(b,\pmb{1}),(c,c),(c,\pmb{1}),(\pmb{1},\pmb{1})\}
\end{equation*}
The operation tables for \(\lor\) and \(\land\) on \(L\) are:
\begin{equation*}
\begin{array}{cc}
\begin{array}{c|ccccc}
\lor & \pmb{0} & a & b & c & \pmb{1} \\
\hline
\pmb{0} & \pmb{0} & a & b & c & \pmb{1} \\
a & a & a & \pmb{1} & \pmb{1} & \pmb{1} \\
b & b & \pmb{1} & b & \pmb{1} & \pmb{1} \\
c & c & \pmb{1} & \pmb{1} & c & \pmb{1} \\
\pmb{1} & \pmb{1} & \pmb{1} & \pmb{1} & \pmb{1} & \pmb{1} \\
\end{array}
&
\begin{array}{c|ccccc}
\land & \pmb{0} & a & b & c & \pmb{1} \\
\hline
\pmb{0} & \pmb{0} & \pmb{0} & \pmb{0} & \pmb{0} & \pmb{0} \\
a & \pmb{0} & a & \pmb{0} & \pmb{0} & a \\
b & \pmb{0} & \pmb{0} & b & \pmb{0} & b \\
c & \pmb{0} & \pmb{0} & \pmb{0} & c & c \\
\pmb{1} & \pmb{0} & a & b & c & \pmb{1} \\
\end{array}\\
\end{array}
\end{equation*}
Since every pair of elements in
\(L\) has both a join and a meet,
\([L; \lor , \land ]\) is a lattice (under divides). Is this lattice distributive? We note that:
\(a \lor (c \land b) = a \lor \pmb{0} = a\) and
\((a \lor c) \land (a \lor b) = \pmb{1} \land \pmb{1} = \pmb{1}\text{.}\) Therefore,
\(a \lor (b \land c) \neq (a \lor b) \land (a \lor c)\) for some values of
\(a, b, c \in L\text{.}\) Thus, this lattice is not distributive.