Definition 4.1.1. Counterexample.
An example that disproves a statement is called a counterexample.
Section 4.1 Methods of Proof for Sets
If \(A\text{,}\) \(B\text{,}\) and \(C\) are arbitrary sets, is it always true that \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\text{?}\) There are a variety of ways that we could attempt to prove that this distributive law for intersection over union is indeed true. We start with a common “non-proof” and then work toward more acceptable methods.
Subsection 4.1.1 Examples and Counterexamples
We could, for example, let \(A = \{1, 2\}\text{,}\) \(B = \{5, 8, 10\}\text{,}\) and \(C = \{3, 2, 5\}\text{,}\) and determine whether the distributive law is true for these values of \(A\text{,}\) \(B\text{,}\) and \(C\text{.}\) In doing this we will have only determined that the distributive law is true for this one example. It does not prove the distributive law for all possible sets \(A\text{,}\) \(B\text{,}\) and \(C\) and hence is an invalid method of proof. However, trying a few examples has considerable merit insofar as it makes us more comfortable with the statement in question. Indeed, if the statement is not true for the example, we have disproved the statement.
Example 4.1.2. Disproving distributivity of addition over multiplication.
From basic algebra we learned that multiplication is distributive over addition. Is addition distributive over multiplication? That is, is \(a + (b \cdot c) = (a + b) \cdot (a + c)\) always true? If we choose the values \(a = 3\text{,}\) \(b = 4\text{,}\) and \(c = 1\text{,}\) we find that \(3 + (4 \cdot 1) \neq (3 + 4)\cdot (3 + 1)\text{.}\) Therefore, this set of values serves as a counterexample to a distributive law of addition over multiplication.
Subsection 4.1.2 Proof Using Venn Diagrams
In this method, we illustrate both sides of the statement via a Venn diagram and determine whether both Venn diagrams give us the same “picture,” For example, the left side of the distributive law is developed in Figure 4.1.3 and the right side in Figure 4.1.4. Note that the final results give you the same shaded area.
The advantage of this method is that it is relatively quick and mechanical. The disadvantage is that it is workable only if there are a small number of sets under consideration. In addition, it doesn’t work very well in a static environment like a book or test paper. Venn diagrams tend to work well if you have a potentially dynamic environment like a blackboard or video.
Development of the left side of the distributive law for sets
Development of the right side of the distributive law for sets
Subsection 4.1.3 Proof using Set-membership Tables
Let \(A\) be a subset of a universal set \(U\) and let \(u\in U\text{.}\) To use this method we note that exactly one of the following is true: \(u \in A\) or \(u\notin A\text{.}\) Denote the situation where \(u \in A\) by 1 and that where \(u \notin A\) by 0. Working with two subsets of \(U\text{,}\) \(A\) and \(B\text{,}\) and \(u \in U\text{,}\) there are four possible anwers to “Where is \(u\text{?}\)” What are they? The set-membership table for \(A \cup B\) is:
| \(A\) | \(B\) | \(A \cup B\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
In order to prove the distributive law via a set-membership table, write out the table for each side of the set statement to be proved and note that if \(S\) and \(T\) are two columns in a table, then the set statement \(S\) is equal to the set statement \(T\) if and only if corresponding entries in each row are the same.
To prove \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\text{,}\) first note that the statement involves three sets, \(A\text{,}\) \(B\text{,}\) and \(C\text{,}\) so there are \(2^3= 8\) possibilities for the membership of an element in the sets.
| \(A\) | \(B\) | \(C\) | \(B \cup C\) | \(A \cap B\) | \(A \cap C\) | \(A \cap (B \cup C)\) | \((A \cap B) \cup (A \cap C)\) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Since each entry in Column 7 is the same as the corresponding entry in Column 8, we have shown that \(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\) for any sets \(A\text{,}\) \(B\text{,}\) and \(C\text{.}\) The main advantage of this method is that it is mechanical. The main disadvantage is that it is reasonable to use only for a relatively small number of sets. If we are trying to prove a statement involving five sets, there are \(2^5 = 32\) rows, which would test anyone’s patience doing the work by hand.
Subsection 4.1.4 Proof Using Definitions
This method involves using definitions and basic concepts to prove the given statement. This procedure forces one to learn, relearn, and understand basic definitions and concepts. It helps individuals to focus their attention on the main ideas of each topic and therefore is the most useful method of proof. One does not learn a topic by memorizing or occasionally glancing at core topics, but by using them in a variety of contexts. The word proof panics most people; however, everyone can become comfortable with proofs. Do not expect to prove every statement immediately. In fact, it is not our purpose to prove every theorem or fact encountered, only those that illustrate methods and/or basic concepts. Throughout the text we will focus in on main techniques of proofs. Let’s illustrate by proving the distributive law.
Proof Technique 1. State or restate the theorem so you understand what is given (the hypothesis) and what you are trying to prove (the conclusion).
Theorem 4.1.7. The Distributive Law of Intersection over Union.
If \(A\text{,}\) \(B\text{,}\) and \(C\) are sets, then \(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\text{.}\)
Proof.
What we are to prove: \(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\text{.}\)
Commentary: What types of objects am I working with: sets? real numbers? propositions? The answer is sets: sets of elements that can be anything you care to imagine. The universe from which we draw our elements plays no part in the proof of this theorem.
We need to show that the two sets are equal. Let’s call them the left-hand set \((LHS\)) and the right-hand set (\(RHS\)). To prove that \(LHS = RHS\text{,}\) we must prove two things: (a) \(LHS\subseteq RHS\text{,}\) and (b) \(RHS \subseteq LHS\text{.}\)
To prove part a and, similarly, part b, we must show that each element of \(LHS\) is an element of \(RHS\text{.}\) Once we have diagnosed the problem we are ready to begin.
We must prove: (a) \(A \cap (B \cup C)\subseteq (A\cap B) \cup (A\cap C)\text{.}\)
Let \(x \in A\cap (B \cup C)\text{:}\)
\begin{equation*}
\begin{split}
x \in A \cap (B \cup C) & \Rightarrow x\in A \textrm{ and } (x\in B\textrm{ or } x\in C)\\
& \quad \textrm{def. of union and intersection}\\
& \Rightarrow (x \in A\textrm{ and }x\in B)\textrm{ or } (x\in A\textrm{ and }x\in C)\\
&\quad \textrm{distributive law of logic}\\
& \Rightarrow (x \in A \cap B) \textrm{ or } (x \in A \cap C)\\
&\quad \textrm{def. of intersection}\\
& \Rightarrow x \in (A \cap B) \cup (A \cap C)\\
&\quad \textrm{def. of union}
\end{split}
\end{equation*}
We must also prove (b) \((A\cap B) \cup (A\cap C)\subseteq A \cap (B \cup C)\text{.}\)
\begin{equation*}
\begin{split}
x\in (A\cap B) \cup (A \cap C)& \Rightarrow (x\in A\cap B)\text{or } (x\in A\cap C)\\
&\quad \textrm{ Why? } \\
& \Rightarrow (x\in A\textrm{ and }x\in B)\textrm{ or } (x\in A\textrm{ and }x\in C)\\
&\quad\textrm{ Why? }\\
&\Rightarrow x\in A \textrm{ and } (x\in B\textrm{ or }x\in C)\\
&\quad\textrm{ Why? }\\
&\Rightarrow x\in A\cap (B\cup C)\\
&\quad\textrm{ Why? } \square
\end{split}\text{.}
\end{equation*}
Proof Technique 2
-
To prove that \(A\subseteq B\text{,}\) we must show that if \(x \in A\text{,}\) then \(x \in B\text{.}\)
-
To prove that \(A = B\text{,}\) we must show:
To further illustrate the Proof-by-Definition technique, let’s prove the following theorem.
Theorem 4.1.8. Another Proof using Definitions.
If \(A\text{,}\) \(B\text{,}\) and \(C\) are any sets, then \(A \times (B \cap C) = (A \times B) \cap (A \times C)\text{.}\)
Proof.
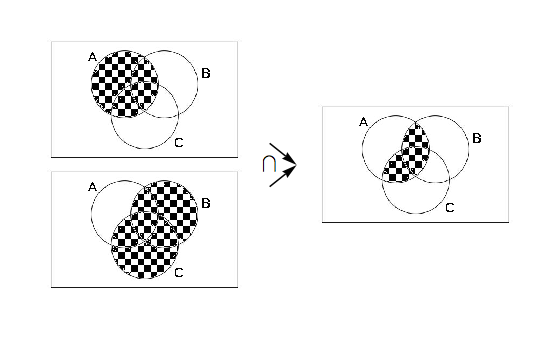
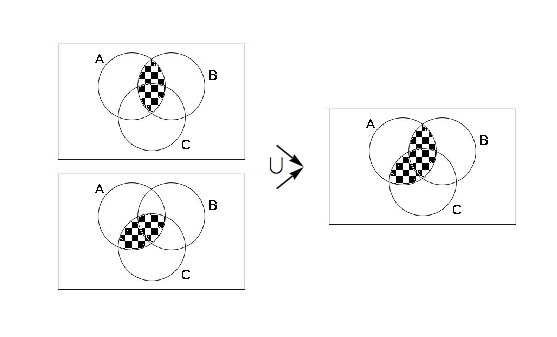
Commentary; We again ask ourselves: What are we trying to prove? What types of objects are we dealing with? We realize that we wish to prove two facts: (a) \(LHS\subseteq RHS\text{,}\) and (b) \(RHS\subseteq LHS\text{.}\)
To prove part (a), and similarly part (b), we’ll begin the same way. Let \(\_\_\_ \in LHS\) to show \(\_\_\_ \in RHS\text{.}\) What should \(\_\_\_\) be? What does a typical object in the \(LHS\) look like?
Now, on to the actual proof.
(a) \(A\times (B\cap C)\subseteq (A\times B)\cap (A\times C)\text{.}\)
Let \((x, y) \in A\times (B\cap C)\text{.}\)
\begin{equation*}
\begin{split}
(x, y) \in A\times (B\cap C) &\Rightarrow x \in A \textrm{ and } y \in (B\cap C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow x \in A \textrm{ and }(y \in B\textrm{ and } y \in C)\\
&\textrm{ Why? }\\
&\Rightarrow (x \in A \textrm{ and } y \in B) \textrm{ and } (x \in A \textrm{ and } y \in C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow (x, y) \in (A\times B) \textrm{ and } (x, y) \in (A \times C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow (x, y) \in (A\times B) \cap (A\times C)\\
&\quad \textrm{ Why? }
\end{split}
\end{equation*}
(b) \((A\times B)\cap (A\times C)\subseteq A\times ( B\cap C)\text{.}\)
Let \((x, y) \in (A\times B) \cap (A\times C)\text{.}\)
\begin{equation*}
\begin{split}
(x, y) \in (A\times B)\cap (A\times C) &\Rightarrow (x, y) \in A\times B\textrm{ and } (x, y) \in A\times C\\
&\quad \textrm{ Why? }\\
&\Rightarrow (x \in A \textrm{ and } y \in B) \textrm{ and } (x \in A \textrm{ and } y \in C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow x \in A \textrm{ and } (y \in B\textrm{ and } y \in C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow x \in A\textrm{ and } y \in (B\cap C)\\
&\quad \textrm{ Why? }\\
&\Rightarrow (x, y) \in A \times (B\cap C)\\
&\quad \textrm{ Why? }
\end{split}
\end{equation*}
Exercises 4.1.5 Exercises
1.
Prove the following:
-
Let \(A\text{,}\) \(B\text{,}\) and \(C\) be sets. If \(A\subseteq B\) and \(B\subseteq C\text{,}\) then \(A\subseteq C\text{.}\)
-
Let \(A,B, \textrm{ and } C\) be sets. If (\(A\subseteq B\) and \(A\subseteq C\)) then \(A\subseteq B\cap C\text{.}\)
-
Let \(A,B, \textrm{ and } C\) be sets. If \(A\subseteq B\) then \(A\times C \subseteq B\times C\text{.}\)
Answer.
-
Assume that \(x\in A\) (condition of the conditional conclusion \(A \subseteq C\)). Since \(A \subseteq B\text{,}\) \(x\in B\) by the definition of \(\subseteq\text{.}\) \(B\subseteq C\) and \(x\in B\) implies that \(x\in C\text{.}\) Therefore, if \(x\in A\text{,}\) then \(x\in C\text{.}\) \(\square\)
-
(Proof that \(A -B \subseteq A\cap B^c\)) Let \(x\) be in \(A - B\text{.}\) Therefore, x is in \(A\text{,}\) but it is not in B; that is,\(\text{ }x \in A\) and \(x \in B^c \Rightarrow x\in A\cap B^c\text{.}\) \(\square\)
-
\((\Rightarrow )\)Assume that \(A \subseteq B\) and \(A \subseteq C\text{.}\) Let \(x\in A\text{.}\) By the two premises,\(x\in B\) and \(x\in C\text{.}\) Therefore, by the definition of intersection, \(x\in B\cap C\text{.}\) \(\square\)
-
\((\Rightarrow )\)(Indirect) Assume that \(B^c\) is not a subset of \(A^c\) . Therefore, there exists \(x\in B^c\) that does not belong to \(A^c\text{.}\) \(x \notin A^c \Rightarrow x \in A\text{.}\) Therefore, \(x\in A\) and \(x\notin B\text{,}\) a contradiction to the assumption that \(A\subseteq B\text{.}\) \(\square\)
-
There are two cases to consider. The first is when \(C\) is empty. Then the conclusion follows since both Cartesian products are empty.If \(C\) isn’t empty, we have two subcases, if \(A\) is empty, \(A\times C = \emptyset\text{,}\) which is a subset of every set. Finally, the interesting subcase is when \(A\) is not empty. Now we pick any pair \((a,c) \in A\times C\text{.}\) This means that \(a\) is in \(A\) and \(c\) is in \(C\text{.}\) Since \(A\) is a subset of \(B\text{,}\) \(a\) is in \(B\) and so \((a,c) \in B \times C\text{.}\) Therefore \(A\times C \subseteq B\times C\text{.}\) \(\square\)
2.
For any integer \(k\text{,}\) let \(k \mathbb{Z}=\{k\cdot j \mid j \in \mathbb{Z}\}\text{,}\) the multiples of \(k\text{.}\)
-
Prove that \(2\mathbb{Z} \cap 3\mathbb{Z} = 6 \mathbb{Z}\text{.}\)
-
Is it true that \(2\mathbb{Z} \cap 4\mathbb{Z} = 8 \mathbb{Z}\text{?}\) Explain your answer.
3.
Disprove the following, assuming \(A, B, \textrm{ and } C\) are sets:
-
\(A - B = B - A\text{.}\)
-
\(A\times B = B\times A\text{.}\)
-
\(\displaystyle A \oplus (B\cap C) = (A \oplus B)\cap (A \oplus C)\)
Answer.
-
If \(A = \mathbb{Z}\) and \(B=\emptyset\text{,}\) \(A - B = \pmb{\mathbb{Z}}\text{,}\) while \(B - A = \emptyset\text{.}\)
-
If \(A=\{0\}\) and \(B = \{1\}\text{,}\) \((0,1) \in A \times B\text{,}\) but \((0, 1)\) is not in \(B\times A\text{.}\)
-
If \(A = \{1\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\emptyset\text{,}\) then the left hand side of the identity is \(\{1\}\) while the right hand side is the empty set. Another example is \(A = \{1,2\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\{2\}.\)
4.
Let \(A, B, \textrm{ and } C\) be sets. Write the following in “if . . . then . . .” language and prove:
5.
Prove by induction that if \(A\text{,}\) \(B_1\text{,}\) \(B_2\text{,}\) ... , \(B_n\) are sets, \(n\geq 2\text{,}\) then \(A\cap ( B_1 \cup B_2\cup \dots \cup B_n) = (A \cap B_1) \cup (A \cap B_2 ) \cup \dots \cup (A\cap B_n)\text{.}\)
Solution.
Proof: Let \(p(n)\) be
\begin{equation*}
A\cap (B_1\cup B_2\cup \cdots \cup B_n)=(A\cap B_1)\cup (A\cap B_2)\cup \cdots \cup (A\cap B_n)\text{.}
\end{equation*}
Basis: We must show that \(p(2) : A \cap (B_1 \cup B_2 )=(A\cap B_1) \cup (A\cap B_2)\) is true. This was done by several methods in section 4.1.
Induction: Assume for some \(n\geq 2\) that \(p(n)\) is true. Then
\begin{equation*}
\begin{split}
A\cap (B_1\cup B_2\cup \cdots \cup B_{n+1})&=A\cap ((B_1\cup B_2\cup \cdots \cup B_n)\cup B_{n+1})\\
&=(A \cap (B_1\cup B_2\cup \cdots \cup B_n))\cup (A\cap B_{n+1}) \quad \textrm{by } p(2)\\
&=((A\cap B_1)\cup \cdots \cup (A\cap B_n))\cup (A\cap B_{n+1})\quad \textrm{by the induction hypothesis}\\
&=(A\cap B_1)\cup \cdots \cup (A\cap B_n)\cup (A\cap B_{n+1})\quad \square\\
\end{split}
\end{equation*}
6.
Let \(A\text{,}\) \(B\) and \(C\) be sets. Prove or disprove:
\begin{equation*}
A \cap B \neq \emptyset, B \cap C \neq \emptyset \Rightarrow A\cap C \neq \emptyset
\end{equation*}
Answer.
The statement is false. The sets \(A=\{1,2\}\text{,}\) \(B=\{2,3\}\) and \(C=\{3,4\}\) provide a counterexample. Looking ahead to Chapter 6, we would say that the relation of being non-disjoint is not transitive 6.3.3
You have attempted of activities on this page.
