Section2.1Basic Counting Techniques - The Rule of Products
Subsection2.1.1What is Combinatorics?
One of the first concepts our parents taught us was the “art of counting.” We were taught to raise three fingers to indicate that we were three years old. The question of “how many” is a natural and frequently asked question. Combinatorics is the “art of counting.” It is the study of techniques that will help us to count the number of objects in a set quickly. Highly sophisticated results can be obtained with this simple concept. The following examples will illustrate that many questions concerned with counting involve the same process.
Example2.1.1.How many lunches can you have?
A snack bar serves five different sandwiches and three different beverages. How many different lunches can a person order? One way of determining the number of possible lunches is by listing or enumerating all the possibilities. One systematic way of doing this is by means of a tree, as in the following figure.
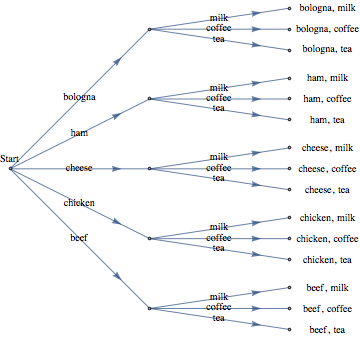
Figure2.1.2.Tree diagram to enumerate the number of possible lunches.
Every path that begins at the position labeled START and goes to the right can be interpreted as a choice of one of the five sandwiches followed by a choice of one of the three beverages. Note that considerable work is required to arrive at the number fifteen this way; but we also get more than just a number. The result is a complete list of all possible lunches. If we need to answer a question that starts with “How many . . . ,” enumeration would be done only as a last resort. In a later chapter we will examine more enumeration techniques.
An alternative method of solution for this example is to make the simple observation that there are five different choices for sandwiches and three different choices for beverages, so there are \(5 \cdot 3 = 15\) different lunches that can be ordered.
Example2.1.3.Counting elements in a cartesian product.
Let \(A = \{a, b, c, d, e\}\) and \(B = \{1,2,3\}\text{.}\) From Chapter 1 we know how to list the elements in \(A \times B = \{(a, 1), (a, 2), (a, 3), ..., (e, 3)\}\text{.}\) Since the first entry of each pair can be any one of the five elements \(a, b, c, d\text{,}\) and \(e\text{,}\) and since the second can be any one of the three numbers 1, 2, and 3, it is quite clear there are \(5 \cdot 3 = 15\) different elements in \(A \times B\text{.}\)
Example2.1.4.A True-False Questionnaire.
A person is to complete a true-false questionnaire consisting of ten questions. How many different ways are there to answer the questionnaire? Since each question can be answered in either of two ways (true or false), and there are ten questions, there are
different ways of answering the questionnaire. The reader is encouraged to visualize the tree diagram of this example, but not to draw it!
We formalize the procedures developed in the previous examples with the following rule and its extension.
Subsection2.1.2The Rule Of Products
Theorem2.1.5.The Rule Of Products.
If two operations must be performed, and if the first operation can always be performed \(p_1\) different ways and the second operation can always be performed \(p_2\) different ways, then there are \(p_1 p_2\) different ways that the two operations can be performed.
Note: It is important that \(p_2\) does not depend on the option that is chosen in the first operation. Another way of saying this is that \(p_2\) is independent of the first operation. If \(p_2\) is dependent on the first operation, then the rule of products does not apply.
Example2.1.6.Reduced Lunch Possibilities.
Assume in Example 2.1.1, coffee is not served with a beef or chicken sandwiches. Then by inspection of Figure 2.1.2 we see that there are only thirteen different choices for lunch. The rule of products does not apply, since the choice of beverage depends on one’s choice of a sandwich.
The rule of products can be extended to include sequences of more than two operations.
Theorem2.1.7.Extended Rule Of Products.
If \(n\) operations must be performed, and the number of options for each operation is \(p_1\text{,}\)\(p_2, \dots, p_n\) respectively, with each \(p_i\) independent of previous choices, then the \(n\) operations can be performed \(p_1 \cdot p_2 \cdot \cdots \cdot p_n\) different ways.
Example2.1.8.A Multiple Choice Questionnaire.
A questionnaire contains four questions that have two possible answers and three questions with five possible answers. Since the answer to each question is independent of the answers to the other questions, the extended rule of products applies and there are \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5 = 2^4 \cdot 5^3 = 2000 \) different ways to answer the questionnaire.
In Chapter 1 we introduced the power set of a set \(A\text{,}\)\(\mathcal{P}(A)\text{,}\) which is the set of all subsets of \(A\text{.}\) Can we predict how many elements are in \(\mathcal{P}(A)\) for a given finite set \(A\text{?}\) The answer is yes, and in fact if \(\lvert A \rvert = n\text{,}\) then \(\lvert \mathcal{P}(A) \rvert = 2^{n}\text{.}\) The ease with which we can prove this fact demonstrates the power and usefulness of the rule of products. Do not underestimate the usefulness of simple ideas.
Theorem2.1.9.Power Set Cardinality Theorem.
If \(A\) is a finite set, then \(\lvert \mathcal{P}(A) \rvert = 2^{\lvert A \rvert }\text{.}\)
Proof.
Proof: Consider how we might determine any \(B \in \mathcal{P}(A)\text{,}\) where \(\lvert A \rvert =n\text{.}\) For each element \(x \in A\) there are two choices, either \(x \in B\) or \(x \notin B\text{.}\) Since there are \(n\) elements of \(A\) we have, by the rule of products,
different subsets of \(A\text{.}\) Therefore, \(\mathcal{P}(A)= 2^{n}\text{.}\)
Exercises2.1.3Exercises
1.
In horse racing, to bet the “daily double” is to select the winners of the first two races of the day. You win only if both selections are correct. In terms of the number of horses that are entered in the first two races, how many different daily double bets could be made?
Answer.
If there are \(m\) horses in race 1 and \(n\) horses in race 2 then there are \(m \cdot n\) possible daily doubles.
2.
Professor Shortcut records his grades using only his students’ first and last initials. What is the smallest class size that will definitely force Prof. S. to use a different system?
Answer.
There are \(26^2\) possible first initial/last initial pairs. If there are at least \(26^2+1 = 677\) students then surely, there will be at least two students with the same initials. Of course, a realistic number is much lower since many initial pairs are very rare and some are quite common.
3.
A certain shirt comes in four sizes and six colors. One also has the choice of a dragon, an alligator, or no emblem on the pocket. How many different shirts could you order?
Answer.
\(72=4\cdot 6\cdot 3\)
4.
A builder of modular homes would like to impress his potential customers with the variety of styles of his houses. For each house there are blueprints for three different living rooms, four different bedroom configurations, and two different garage styles. In addition, the outside can be finished in cedar shingles or brick. How many different houses can be designed from these plans?
Answer.
There are \(3 \times 4 \times 2 \times 2 = 48\) different designs.
5.
The Pi Mu Epsilon mathematics honorary society of Outstanding University wishes to have a picture taken of its six officers. There will be two rows of three people. How many different way can the six officers be arranged?
Answer.
\(720=6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1\)
6.
An automobile dealer has several options available for each of three different packages of a particular model car: a choice of two styles of seats in three different colors, a choice of four different radios, and five different exteriors. How many choices of automobile does a customer have?
Answer.
There are \(2 \times 3 \times 4 \times 5 = 120\) different choices for a customer.
7.
A clothing manufacturer has put out a mix-and-match collection consisting of two blouses, two pairs of pants, a skirt, and a blazer. How many outfits can you make? Did you consider that the blazer is optional? How many outfits can you make if the manufacturer adds a sweater to the collection?
Answer.
If we always include the blazer in the outfit we would have 6 outfits. If we consider the blazer optional then there would be 12 outfits. When we add a sweater we have the same type of choice. Considering the sweater optional produces 24 outfits.
8.
As a freshman, suppose you had to take two of four lab science courses, one of two literature courses, two of three math courses, and one of seven physical education courses. Disregarding possible time conflicts, how many different schedules do you have to choose from?
Answer.
The only tricky thing about this problem is that in choosing the two lab science courses, there are just six possible choices. This is because the order in which the courses are selected isn’t indicated as being significant. For example, if chemistry and biology are among the courses, choosing chamistry and then biology is the same as choosing biology and then chemistry, so although it may appear that there are \(4 \times 3\) ways of picking lab science courses, there are only half that many. The number of ways to select other courses is more obvous. For the math courses, there are three choices because we need only decide which course to not take. So the number of ways to pick courses (not taking into account times) is \(6 \times 2 \times 3 \times 7 = 252\text{.}\)
9.
(a) Suppose each single character stored in a computer uses eight bits. Then each character is represented by a different sequence of eight 0’s and 1’s called a bit pattern. How many different bit patterns are there? (That is, how many different characters could be represented?)
(b) How many bit patterns are palindromes (the same backwards as forwards)?
(c) How many different bit patterns have an even number of 1’s?
Answer.
\(\displaystyle 2^8=256\)
\(2^4=16\text{.}\) Here we are concerned only with the first four bits, since the last four are a mirror image of the first four.
\(2^7=128\text{,}\) you have no choice in the last bit.
10.
Automobile license plates in Massachusetts usually consist of three digits followed by three letters. The first digit is never zero. How many different plates of this type could be made?
Answer.
The number of possible license plates is is \(9 \times 10^2 \times 26^3 = 15,818,400\text{.}\)
11.
Let \(A = \{1, 2, 3, 4\}\text{.}\) Determine the number of different subsets of \(A\text{.}\)
Let \(A = \{1, 2, 3, 4, 5\}\text{.}\) Determine the number of proper subsets of \(A\text{.}\)
Answer.
\(\displaystyle 16\)
\(\displaystyle 31\)
In the second part we can arrive at the answer by counting all subsets and subtracting one since one of the sets (the whole set) is an improper subsets.
12.
How many integers from 100 to 999 can be written in base ten without using the digit 7?
Answer.
The hundreths digit can be any of 8 different values while we have 9 choices for the other two digits, so the number of possibilities is \(8 \times 9^2 = 648\)
13.
Consider three persons, A, B, and C, who are to be seated in a row of three chairs. Suppose A and B are identical twins. How many seating arrangements of these persons can there be
If you are a total stranger?
If you are A and B’s mother?
This problem is designed to show you that different people can have different correct answers to the same problem.
Answer.
\(\displaystyle 3\)
\(\displaystyle 6\)
14.
How many ways can a student do a ten-question true-false exam if he or she can choose not to answer any number of questions?
Answer.
Each question can be answered three ways: true, false or blank. There are \(3^{10} = 59049\) ways to answer the whole exam.
15.
Suppose you have a choice of fish, lamb, or beef for a main course, a choice of peas or carrots for a vegetable, and a choice of pie, cake, or ice cream for dessert. If you must order one item from each category, how many different dinners are possible?
Answer.
\(18\)
16.
Suppose you have a choice of vanilla, chocolate, maple walnut or strawberry for ice cream, a choice of peanuts or walnuts for chopped nuts, and a choice of hot fudge or marshmallow for topping. You don’t have to order nuts. How many different sundaes are possible?
Answer.
There are \(4 \times 3 \times 2\) ways to order a sundae. The factor of three accounts for the possible choices for nuts, one of which is to not order them.
17.
A questionnaire contains six questions each having yes-no answers. For each yes response, there is a follow-up question with four possible responses.
Draw a tree diagram that illustrates how many ways a single question in the questionnaire can be answered.
Six people are invited to a dinner party. How many ways are there of seating them at a round table? If the six people consist of three who identify as male and three who identify as female, how many ways are there of seating them if each male must be surrounded by two females? Assume we are only concerned with the relative positions around the table. So if we rotate everyone we wouldn’t consider this a change in the seating.
Answer.
With no restrictions on seating, we can select any person in the party and seat them at the table. Then to their left we have five choices for seating someone and next to the left there are 4 choices, etc. The number of choices in all is then \(5 \times 4 \times 3 \times 2 = 120\text{.}\) With the alternate male/female scheme, if we seat any male, there are three choices for the female to the left, two choices for the male who is further left, two choices for the female to the right and the other two individuals have their seats determined at this point. So the number of possibilities is \(3 \times 2^2 = 12\text{.}\)
19.
How many ways can you separate a set with \(n\) elements into two nonempty subsets if the order of the subsets is immaterial? What if the order of the subsets is important?
Answer.
\(2^{n-1}-1\) and \(2^n-2\)
20.
A gardener has three flowering shrubs and four nonflowering shrubs, where all shrubs are distinguishable from one another. He must plant these shrubs in a row using an alternating pattern, that is, a shrub must be of a different type from that on either side. How many ways can he plant these shrubs? If he has to plant these shrubs in a circle using the same pattern, how many ways can he plant this circle? Note that one nonflowering shrub will be left out at the end.
Answer.
If you arrange the shrubs in a row, the nonflowering shrubs must be in positions 1, 3, 5 and 7. We assume that reversing the order would be considered different. So the number of orderings of the nonflowering shubs would be \(4 \times 3 \times 2 \times 1 = 24\text{.}\) The flowering shrubs in positions 22, 4 and 6 can be arranged \(3 \times 2 \times 1 = 6\) ways and so the number of possible row arrangements is \(24 \times 6 = 144\text{.}\) For the circular arrangement, we can decide which nonflowering shrub to not include in the arrangement four ways. Once we have done this, we have the same situation as the dinner party above where we specified male/female alternation. So there are 12 ways to arrange the shrubs. Therefore we have \(4 \times 12 = 48\) possible arrangements of the shrubs in a circle. Let’s put the remaining one in the center!
