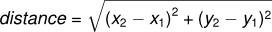How to Think Like a Computer Scientist The PreTeXt Interactive Edition

At this point, you should be able to look at complete functions and tell what they do. Also, if you have been doing the exercises, you have written some small functions. As you write larger functions, you might start to have more difficulty, especially with runtime and semantic errors.

To deal with increasingly complex programs, we are going to suggest a technique called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.

As an example, suppose you want to find the distance between two points, given by the coordinates (x1, y1) and (x2, y2). By the Pythagorean theorem, the distance is:

The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?

In this case, the two points are the inputs, which we can represent using four parameters. The return value is the distance, which is a floating-point value.

Already we can write an outline of the function that captures our thinking so far.

def distance(x1, y1, x2, y2):
    return 0.0

Obviously, this version of the function doesn’t compute distances; it always returns zero. But it is syntactically correct, and it will run, which means that we can test it before we make it more complicated.

We import the test module to enable us to write a unit test for the function.

The testEqual function from the test module calls the distance function with sample inputs: (1,2, 1,2). The first 1,2 are the coordinates of the first point and the second 1,2 are the coordinates of the second point. What is the distance between these two points? Zero. testEqual compares what is returned by the distance function and the 0 (the correct answer).

When testing a function, it is essential to know the right answer.

For the second test the horizontal distance equals 3 and the vertical distance equals 4; that way, the result is 5 (the hypotenuse of a 3-4-5 triangle). For the third test, we have a 1-1-sqrt(2) triangle.

At this point we have confirmed that the function is syntactically correct, and we can start adding lines of code. After each incremental change, we test the function again. If an error occurs at any point, we know where it must be — in the last line we added.

A logical first step in the computation is to find the differences x2- x1 and y2- y1. We will store those values in temporary variables named dx and dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    return 0.0

Next we compute the sum of squares of dx and dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx**2 + dy**2
    return 0.0

Again, we could run the program at this stage and check the value of dsquared (which should be 25).

Finally, using the fractional exponent 0.5 to find the square root, we compute and return the result.

When you start out, you might add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger conceptual chunks. As you improve your programming skills you should find yourself managing bigger and bigger chunks: this is very similar to the way we learned to read letters, syllables, words, phrases, sentences, paragraphs, etc., or the way we learn to chunk music — from indvidual notes to chords, bars, phrases, and so on.

The key aspects of the process are: