Section 5.8 Sierpinski Triangle
Another fractal that exhibits the property of self-similarity is the Sierpinski triangle. An example is shown in Figure 5.8.1. The Sierpinski triangle illustrates a three-way recursive algorithm. The procedure for drawing a Sierpinski triangle by hand is simple. Start with a single large triangle. Divide this large triangle into three new triangles by connecting the midpoint of each side. Ignoring the middle triangle that you just created, apply the same procedure to each of the three corner triangles. Each time you create a new set of triangles, you recursively apply this procedure to the three smaller corner triangles. You can continue to apply this procedure indefinitely if you have a sharp enough pencil. Before you continue reading, you may want to try drawing the Sierpinski triangle yourself, using the method described.

Image of the Sierpinski Triangle, a fractal composed of colored triangles. The main triangle is outlined with progressively smaller triangles in alternating colors of red, green, and white, forming a pattern that repeats at smaller scales. The center of the triangle features a large inverted blue triangle, emphasizing the fractal’s characteristic self-similarity.
Since we can continue to apply the algorithm indefinitely, what is the base case? We will see that the base case is set arbitrarily as the number of times we want to divide the triangle into pieces. Sometimes we call this number the “degree” of the fractal. Each time we make a recursive call, we subtract 1 from the degree until we reach 0. When we reach a degree of 0, we stop making recursive calls. The code that generated the Sierpinski Triangle in Figure 5.8.1 is shown in Task 5.8.1.a.
The program in Task 5.8.1.a follows the ideas outlined above. The first thing
sierpinski does is draw the outer triangle. Next, there are three recursive calls, one for each of the new corner triangles we get when we connect the midpoints. Once again we make use of the standard turtle module that comes with Python. You can learn all the details of the methods available in the turtle module by using help('turtle') from the Python prompt.
Look at the code and think about the order in which the triangles will be drawn. While the exact order of the corners depends upon how the initial set is specified, let’s assume that the corners are ordered lower left, top, lower right. Because of the way the
sierpinski function calls itself, sierpinski works its way to the smallest allowed triangle in the lower-left corner, and then begins to fill out the rest of the triangles working back. Then it fills in the triangles in the top corner by working toward the smallest, topmost triangle. Finally, it fills in the lower-right corner, working its way toward the smallest triangle in the lower right.
Sometimes it is helpful to think of a recursive algorithm in terms of a diagram of function calls. Figure 5.8.2 shows that the recursive calls are always made going to the left. The active functions are outlined in black, and the inactive function calls are in gray. The farther you go toward the bottom of Figure 5.8.2, the smaller the triangles. The function finishes drawing one level at a time; once it is finished with the bottom left it moves to the bottom middle, and so on.
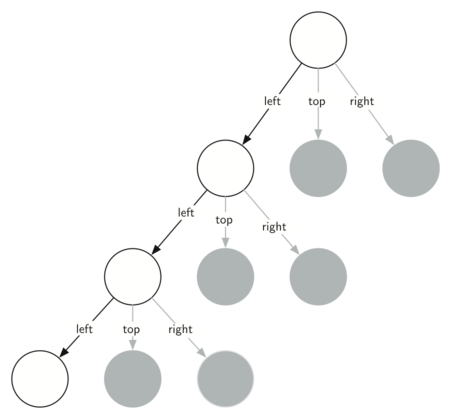
Diagram showing the recursive construction of a Sierpinski Triangle using a tree structure. The diagram starts with a single top circle labeled ’top’, branching out into three interconnected circles labeled ’left’, ’top’, and ’right’. Each of these circles further branches out in a similar pattern, with the process repeating for several iterations. The circles decrease in size from top to bottom, representing the fractal’s recursive nature. The grayscale shading of the circles suggests depth or iteration levels.
The
sierpinski function relies heavily on the middle function. middle takes as arguments two endpoints and returns the point halfway between them. In addition, Task 5.8.1.a has a function that draws a filled triangle using the begin_fill and end_fill turtle methods.
The above sierpinski triangle visualization utilizes C-Turtle, a C++ equivalent of Python’s
turtle library, and can be found on GitHub here: https://github.com/walkerje/C-Turtle/
You have attempted of activities on this page.
