Section 9.17 Topological Sorting
To demonstrate that computer scientists can turn just about anything into a graph problem, let’s consider the difficult problem of stirring up a batch of pancakes. The recipe is really quite simple: 1 egg, 1 cup of pancake mix, 1 tablespoon oil, and \(3 \over 4\) cup of milk. To make pancakes you must heat the griddle, mix all the ingredients together and spoon the mix onto a hot griddle. When the pancakes start to bubble you turn them over and let them cook until they are golden brown on the bottom. Before you eat your pancakes you are going to want to heat up some syrup. Figure 9.17.1 illustrates this process as a graph.
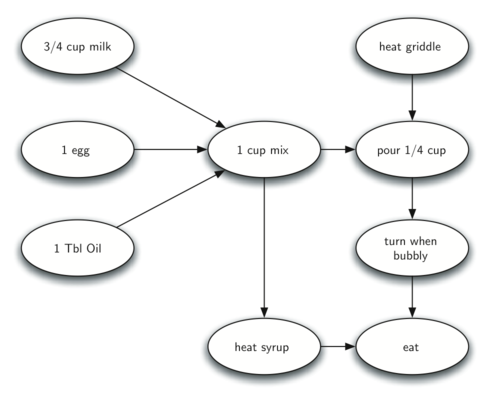
A flowchart detailing the steps for making pancakes. The process begins with three separate ingredients: 3/4 cup of milk, 1 egg, and 1 Tbl of oil, converging into a central step labeled ’1 cup mix’. From there, the flowchart indicates to ’heat griddle’, followed by ’pour 1/4 cup’ of the mix onto the griddle. The next step is to ’turn when bubbly’, indicating when to flip the pancakes. Two concurrent final steps are ’heat syrup’ and ’eat’, signifying the end of the pancake-making process. The flowchart effectively outlines the sequence of actions required to make pancakes from the initial ingredient preparation to the final eating stage.
The difficult thing about making pancakes is knowing what to do first. As you can see from Figure 9.17.1 you might start by heating the griddle or by adding any of the ingredients to the pancake mix. To help us decide the precise order in which we should do each of the steps required to make our pancakes we turn to a graph algorithm called the topological sort.
A topological sort takes a directed acyclic graph and produces a linear ordering of all its vertices such that if the graph \(G\) contains an edge \((v,w)\) then the vertex \(v\) comes before the vertex \(w\) in the ordering. Directed acyclic graphs are used in many applications to indicate the precedence of events. Making pancakes is just one example; other examples include software project schedules, precedence charts for optimizing database queries, and multiplying matrices.
The topological sort is a simple but useful adaptation of a depth first search. The algorithm for the topological sort is as follows:
-
Call
dfs(g)for some graphg. The main reason we want to call depth first search is to compute the finish times for each of the vertices. -
Store the vertices in a list in decreasing order of finish time.
-
Return the ordered list as the result of the topological sort.
Figure 9.17.2 shows the depth first forest constructed by
dfs on the pancake-making graph shown in Figure 9.17.1.
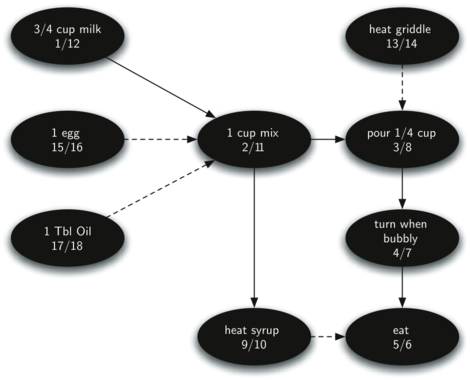
The image depicts the result of a depth-first search on a pancake recipe graph. It starts with "3/4 cup milk" at step 1/12, which along with "1 egg" at step 15/16 and "1 Tbl Oil" at step 17/18, feeds into "1 cup mix" at step 2/11. This leads to "heat griddle" at step 13/14, followed by "pour 1/4 cup" at step 3/8. The next action is "turn when bubbly" at step 4/7, and the final steps are "heat syrup" at step 9/10 and "eat" at step 5/6. Each step is represented by an oval, with directed edges showing the sequence of the recipe steps, and numbers indicating the search progression.
Finally, Figure 9.17.3 shows the results of applying the topological sort algorithm to our graph. Now all the ambiguity has been removed and we know exactly the order in which to perform the pancake making steps.

Alt text for Figure 29: This image shows the result of a topological sort on a directed acyclic graph representing the steps for making pancakes. The sequence begins with "1 Tbl Oil" at step 17/18, followed by "1 egg" at step 15/16, "3/4 cup milk" at step 1/12, and "1 cup mix" at step 2/11. The next steps are "heat griddle" at step 13/14, "heat syrup" at step 9/10, "pour 1/4 cup" at step 3/8, and "turn when bubbly" at step 4/7. The final action is "eat" at step 5/6. Each step is depicted as an oval, connected by directed paths that indicate the order of operations, with numbers denoting the order in the topological sort.
You have attempted of activities on this page.
