Section 9.18 Strongly Connected Components
For the remainder of this chapter we will turn our attention to some extremely large graphs. The graphs we will use to study some additional algorithms are the graphs produced by the connections between hosts on the Internet and the links between web pages. We will begin with web pages.
Search engines like Google and Bing exploit the fact that the pages on the web form a very large directed graph. To transform the World Wide Web into a graph, we will treat a page as a vertex, and the hyperlinks on the page as edges connecting one vertex to another. Figure 9.18.1 shows a very small part of the graph produced by following the links from one page to the next, beginning at Luther College’s Computer Science home page. Of course, this graph could be huge, so we have limited it to web sites that are no more than 10 links away from the CS home page.
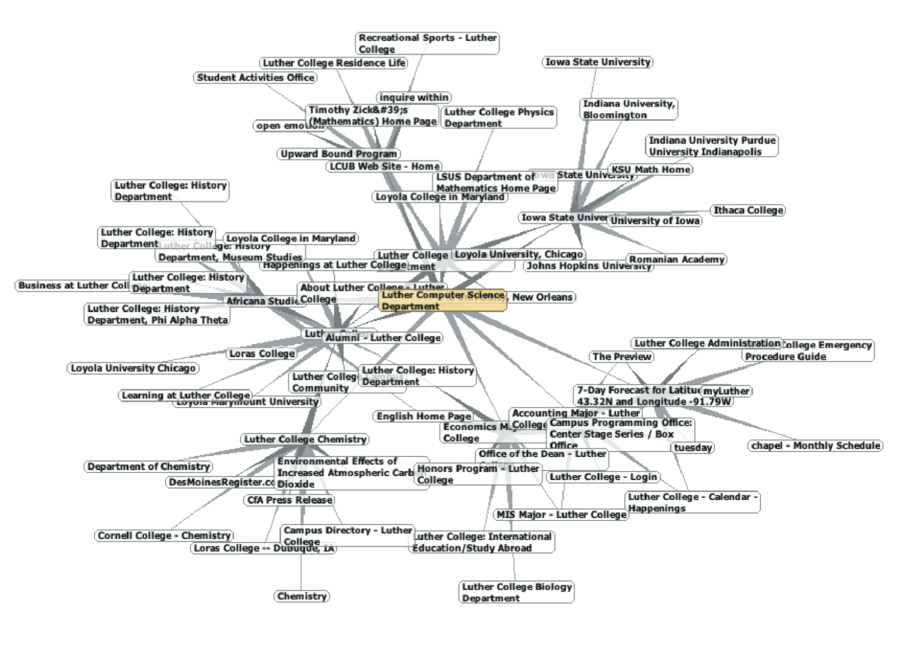
This image depicts a complex network graph that visualizes the web of links from the Luther Computer Science Home Page. The graph is a cluster of interconnected nodes, each representing a different page or external link. Central nodes like "Luther College History Department" have multiple connections radiating out to related nodes such as "Loyola College in Maryland" and "Iowa State University." Peripheral nodes link to a variety of topics, including "Recreational Sports - Luther College," "Luther College Administration," and "Cornell College - Chemistry." The links create a dense web, illustrating the interconnected nature of the website’s structure. The graph is used to demonstrate the relationships and pathways between various academic departments, programs, and external educational institutions.
If you study the graph in Figure 9.18.1 you might make some interesting observations. First you might notice that many of the other web sites on the graph are other Luther College web sites. Second, you might notice that there are several links to other colleges in Iowa. Third, you might notice that there are several links to other liberal arts colleges. You might conclude from this that there is some underlying structure to the web that clusters together web sites that are similar on some level.
One graph algorithm that can help find clusters of highly interconnected vertices in a graph is called the strongly connected components algorithm (SCC). We formally define a strongly connected component, \(C\text{,}\) of a graph \(G\text{,}\) as the largest subset of vertices \(C \subset V\) such that for every pair of vertices \(v, w \in C\) we have a path from \(v\) to \(w\) and a path from \(w\) to \(v\text{.}\) Figure 9.18.2 shows a simple graph with three strongly connected components. The strongly connected components are identified by the different shaded areas.
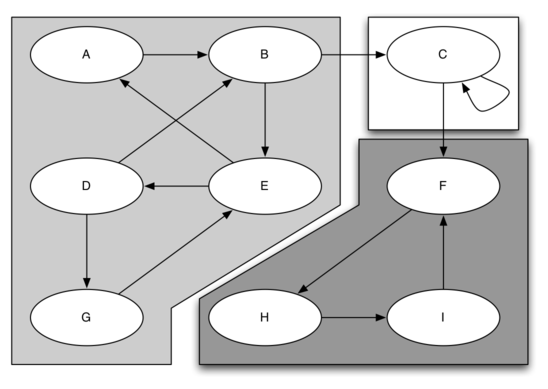
The image shows a directed graph composed of three strongly connected components, each highlighted in a separate shaded area. The graph contains nine nodes labeled A through I. Nodes A, B, and C form the first component, with arrows indicating directed edges from A to B, B to A, and B to C. The second component consists of nodes D, E, and G, with directed edges connecting D to E, E to D, and D to G. The third component includes nodes F, H, and I, with edges from F to H, H to I, and I to F. Each component is a self-contained subgraph where every node is reachable from every other node within the same component, illustrating the concept of strong connectivity in graph theory.
Once the strongly connected components have been identified we can show a simplified view of the graph by combining all the vertices in one strongly connected component into a single larger vertex. The simplified version of the graph in Figure 9.18.2 is shown in Figure 9.18.3.
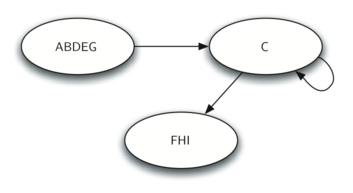
The image depicts a simplified or reduced graph consisting of three nodes, which are labeled with the combined letters of the nodes from the strongly connected components they represent. The first node contains the letters "ABDEG," indicating it is a merged node of the first component. The second node is labeled "C," and the third node contains "FHI," representing the second and third components, respectively. There are directed edges from the "ABDEG" node to "C" and from "C" to "FHI," showing the flow between these combined nodes. This reduced graph emphasizes the hierarchical structure and the dependencies between the strongly connected components of the original directed graph.
Once again we will see that we can create a very powerful and efficient algorithm by making use of a depth first search. Before we tackle the main SCC algorithm we must look at one other definition. The transposition of a graph \(G\) is defined as the graph \(G^T\) where all the edges in the graph have been reversed. That is, if there is a directed edge from node A to node B in the original graph then \(G^T\) will contain and edge from node B to node A. Figure 9.18.4 and Figure 9.18.5 show a simple graph and its transposition.

The image illustrates a directed graph G with four nodes labeled A, B, C, and D. There is a directed edge from A to B, indicating a one-way relationship, and two other directed edges, one from B to D and another from C to D, suggesting that both B and C can independently reach D.
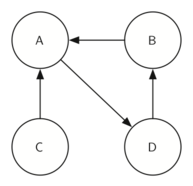
The image shows the transpose of the graph \(G^T\) from Figure 33, where the direction of all the edges in the original graph G has been reversed. In this transposed graph, there is a directed edge from B to A, and two other directed edges, one from D to B and another from D to C, indicating that D can reach both B and C. This represents the inverse relationships compared to the original graph G.
Look at the figures again. Notice that the graph in Figure 9.18.4 has two strongly connected components. Now look at Figure 9.18.5. Notice that it has the same two strongly connected components.
We can now describe the algorithm to compute the strongly connected components for a graph.
-
Compute \(G^T\text{.}\)
-
Call
dfsfor the graph \(G^T\) but in the main loop of DFS explore each vertex in decreasing order of finish time. -
Each tree in the forest computed in step 3 is a strongly connected component. Output the vertex ids for each vertex in each tree in the forest to identify the component.
Let’s trace the operation of the steps described above on the example graph in Figure 9.18.2. Figure 9.18.6 shows the starting and finishing times computed for the original graph by the DFS algorithm. Figure 9.18.7 shows the starting and finishing times computed by running DFS on the transposed graph.

The image displays a directed graph G consisting of nine nodes labeled A through I. Each node is annotated with a pair of numbers, representing the finishing times in the format ’start/finish’. The edges indicate the direction of connection between nodes. Solid arrows represent direct connections, while dashed arrows signify connections that are part of the graph but are not the primary path in the context shown. This graph is likely used to demonstrate an algorithmic concept such as Depth-First Search (DFS), where the numbers indicate the order in which nodes are fully processed.
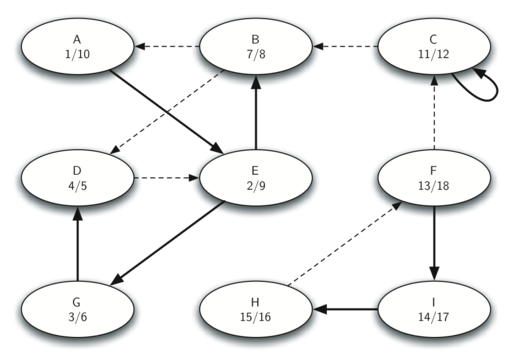
This image depicts a directed graph, labeled G^T, which is the transpose of a previous graph G. It consists of nine nodes labeled A through I. Each node is marked with two numbers, indicating the finishing times, in a format that suggests the order in which they were processed, with the first number likely representing the start time and the second the finish time. The graph is interconnected with solid and dashed arrows indicating the direction of the edges, where the dashed arrows might represent the reverse of the original connections inG. This graph is typically used to demonstrate concepts such as the calculation of finishing times in a Depth-First Search (DFS) on the transposed graph for algorithms like Kosaraju’s or other strong component identification algorithms.
Finally, Figure 9.18.8 shows the forest of three trees produced in step 3 of the strongly connected component algorithm. You will notice that we do not provide you with the Python code for the SCC algorithm, we leave writing this program as an exercise.

The diagram shows a directed graph illustrating the concept of strongly connected components within a network of nodes. Each node is labeled with a letter from A to I and a pair of numbers, which could represent the sequence in which a depth-first search algorithm processed them. The graph is organized with directed edges forming paths between the nodes, suggesting the presence of subgraphs where each node is reachable from every other node within the same subgraph. This kind of representation is commonly used in computer science to illustrate algorithms that identify strongly connected components within a graph, which are maximal sets of vertices with a path to every other vertex in the set.
You have attempted of activities on this page.
