Section 1.12 Object-Oriented Programming in C++: Defining Classes
We stated earlier that C++ is an object-oriented programming language. Object-oriented programming is a programming technique based on real world things such as turtles, airplanes, customers, etc. Each object has its own characteristics or attributes as well as its own set of behaviors.
So far, we have used a number of built-in classes to show examples of data and control structures. One of the most powerful features in an object-oriented programming language is the ability to allow a programmer (problem solver) to create new classes that model data that is needed to solve the problem. Each object created with the class data type is called an instance of the class.
Remember that we use abstract data types to provide the logical description or blueprint for what a data object looks like (its state given by object attributes) and what it can do (its behaviors given by class methods). Defining a class creates the blueprint which defines the behaviors and attributes of objects of that new data type. By building a class that implements an abstract data type, a programmer can take advantage of the abstraction process and at the same time provide the details necessary to actually use the abstraction in a program. Hence, whenever we want to implement an abstract data type, we will do so with a new class which will provide the blueprint or template for all of the objects of that type.
Four key principles are associated with object-oriented programming:
We will highlight each principle via examples.
Subsection 1.12.1 A Fraction Class
A very common example to show the details of implementing a user-defined class is to construct a class to implement the abstract data type
Fraction. We have already seen that C++ provides a number of numeric data types for our use. There are times, however, that it would be most appropriate to be able to create data objects that both look and act like fractions.
A fraction such as \(\frac {3}{5}\) consists of two parts. The top value, known as the numerator, can be any integer. The bottom value, called the denominator, can be any integer greater than 0 (negative fractions have a negative numerator). Although it is possible to create a floating point approximation for any fraction, we would like to represent the fraction using exact values to avoid problems inherent in approximations.
Since defining a class makes a new data type, the operations for the
Fraction type will allow a Fraction data object to behave like any other numeric type. We need to be able to add, subtract, multiply, and divide fractions. We also want to be able to print fractions using the standard “slash” form, for example 3/5. In addition, all fraction methods should return results in their lowest terms so that no matter what computation is performed, we always end up with the most common form.
In C++, we define a new class by providing a name and a set of method definitions that are syntactically similar to function definitions. For example, see Exploration 1.12.1.
provides the framework for us to define the methods. The first method that all classes should provide is the constructor. The constructor defines the way in which data objects are created. It’s considered good practice to have a constructor completely setup a class object, so that it’s impossible to create an object in an invalid state. To create a
Fraction object, we will need to initialize two pieces of data, the numerator and the denominator. In C++, the constructor method is always named with the same name as the class it creates and is shown in Task 1.12.2.a.
Exploration 1.12.2. Constructor for Fraction class.
(a) C++.
class Fraction {
public:
Fraction(int top, int bottom) {
/** Fraction constructor method */
num = top; // setting num's value
den = bottom; // setting den's value
}
private:
int num; // num attribute
int den; // den attribute
};
(b) Python.
class Fraction:
def __init__(self,top,bottom):
self.num = top
self.den = bottom
As described earlier, fractions require two pieces of state data, the numerator and the denominator. The notation
int num outside the constructor defines the fraction object to have an internal data object called num as part of its state. Likewise, int den creates the denominator. The values of the two formal parameters are initially assigned to the state, allowing the new fraction object to know its starting values.
To create an object or instance of the
Fraction class, we must invoke the constructor. This happens by using the name of the class and passing actual values for the necessary state after the variable name. For example, see Exploration 1.12.3.
Exploration 1.12.3. Invoking Constructor.
creates an object called
myfraction representing the fraction \(\frac {3}{5}\) (three-fifths). Figure 1.12.1 shows this object as it is now implemented.
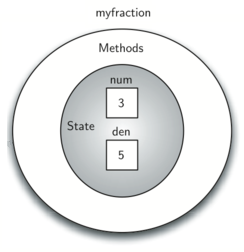
Diagram showing an instance of the Fraction class. The instance is named ’myfraction’ and is depicted as a set of concentric circles. The innermost circle is labeled ’State’ and contains two segments: ’num’ with the number 3 above ’den’ with the number 5, representing the numerator and denominator of a fraction. The middle circle is labeled ’Methods’, indicating the functionality associated with the fraction instance.
Fraction ClassSubsection 1.12.2 Abstraction and Encapsulation
Another way to think about fractions is as “parts of a whole” as shown in the following figure:
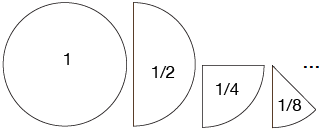
Image showing a visual representation of fractions as "parts of a whole." The diagram begins with a full circle labeled "1," followed by a circle divided into two equal parts labeled "1/2," then into four parts labeled "1/4," and finally into eight parts labeled "1/8." The sequence visually illustrates how a whole can be divided into progressively smaller fractions.
Because we are using classes to create abstract data types, we should probably define the term “abstract” in this context. In object-oriented programming, abstraction requires you to focus solely on the desired properties and behaviors of the objects, discarding everything else that is unimportant or irrelevant. As a result, if we don’t need to consider the “parts of a whole” visual metaphor of a fraction, we won’t include it in the
Fraction class. If a given metaphor is important, we will include it. For our purposes, we want to think of fractions as numbers, so we will avoid using the “parts of a whole” visual metaphor.
The object-oriented principle of encapsulation refers to the practice of grouping or encapsulating related data and the methods that operate on that data into a single unit, typically a class. Encapsulation also requires we hide most of the internal contents of that class, except what is absolutely necessary to expose. Hence, we will restrict the access to our class as much as we can, so that a user can change the class properties and behaviors only from methods provided by the class. C++ allows us to control access with the access keywords
public and private. It is typical in C++ to make all data attributes private and most methods public. All attribute variables under the private keyword will only be able to be accessed by the object’s class methods, not by the user. Only C++’s public methods can be accessed and used by the user. Because we want our user to be able to call every constructor directly, we always place the constructor under public. A third access keyword, protected will be discussed later.
Subsection 1.12.3 Polymorphism
Polymorphism means the ability to appear in many forms. In object-oriented programming, polymorphism refers to the ability to handle objects or methods differently depending on their data type, class, number of arguments, etc. For example, we can overload a constructor with different numbers and types of arguments to give us multiple ways to instantiate an object of a class as shown in Listing 1.12.2 for the
Fraction class.
Fraction(int top, int bottom){
num = top;
den = bottom;
}
Fraction (int top){
num = top;
den = 1;
}
Fraction (){
num = 0;
den = 1;
}
Calling the constructor with two arguments will invoke the first method, calling it with a single argument will invoke the second method, and calling it with no arguments will invoke the third method.
Using optional parameters will accomplish the same task in this case. Since the class will behave the same no matter which implementation you use and the user will have no idea which implementation was chosen, this is an example of encapsulation.
Fraction(int top = 0, int bottom = 1){
num = top;
den = bottom;
}
The next thing we need to do is implement some behaviors that the abstract data type requires. To begin, let’s consider what happens when we try to print a
Fraction object.
int main() {
Fraction myfraction(3, 5);
// Throws an error
cout << myfraction << endl;
return 0;
}
The
fraction object, myfraction, does not know how to respond to this request to print to the console. The cout function requires that the object knows how to interact with the << operator so that the string can be sent to the output stream. Without this, our class will throw an error, which is obviously not what we want.
There are two ways we can solve this problem. One is to define a method called something like
show that will allow the Fraction object to print itself as a string. We can implement this method as shown in Task 1.12.4.a. If we create a Fraction object as before, we can ask it to show itself, in other words, print itself in the proper format by invoking the show method on our fractions.
Exploration 1.12.4. Implementing a show method.
The downside of this approach is that it is not how we expect to print to the console. In C++, there are many operators that are provided for atomic and STL data types that may not work as expected with a user defined class until you overload them. One of these,
<<, is the operator to send data to the output stream. It would be nicer to provide a “better” implementation for this method via operator overloading.
Like function overloading, operator overloading allows us to make operators work for user defined classes by defining a special meaning for that operator when applied to objects of the class as operands. This is a form of polymorphism because it enables the same operator to have different behaviors depending on the class of the objects involved, demonstrating how the same operation can be adapted to various types.
In C++ this new operator needs to be implemented as a friend of the class in order to define the operator’s behavior on objects of the class from a non-class method
<<. Operator overloading is yet another example of polymorphism in object-oriented programming.
A friend function of a class is a function defined outside that class’ scope but with the right to access all private and protected members of the class. In C++, we overload an operator by declaring it a friend function in the class definition and giving it a new implementation. Exploration 1.12.5 shows an example of the
<< operator being overloaded in the Fraction class. Note that stream operators need to return the address of the stream because of the fact that the stream is changed by the stream operator.
Exploration 1.12.5. Operator Overloading Example.
We can overload many other operators for our new
Fraction class. Some of the most important of these are the basic arithmetic operations. We would like to be able to create two Fraction objects and then be able to add them together using the standard “+” notation. At this point, if we try to add two fractions using “+”, we get the following:
Exploration 1.12.6. Error Before Overloading Addition.
(a) C++ Addition Error.
Fraction f1(1, 4); Fraction f2(1, 2); Fraction f3 = f1 + f2; >> error: no match for `operator+' (operand types are `Fraction' and `Fraction'))
(b) Python Addition Error.
f1 = Fraction(1,4) f2 = Fraction(1,2) f1+f2 Traceback (most recent call last): File "<pyshell#173>", line 1, in -toplevel- f1+f2 TypeError: unsupported operand type(s) for +: 'instance' and 'instance'
If you look closely at the error, you see that the problem is that the “+” operator does not understand the
Fraction operands.
We can, of course create something like Exploration 1.12.7.
Exploration 1.12.7. Function for Addition.
which would ask the
Fraction object f1 to add the Fraction object f2 to itself. It would be much better to be written in the standard notation, f1 + f2. We can fix this by providing the Fraction class with a friend that overloads the + operator.
As you know, two fractions must have the same denominator to be added. The easiest way to make sure they have the same denominator is to simply use the product of the two denominators as a common denominator so that \(\frac {a}{b} + \frac {c}{d} = \frac {ad}{bd} + \frac {cb}{bd} = \frac{ad+cb}{bd}\) The implementation is shown in Task 1.12.8.a. The addition function returns a new
Fraction object with the numerator and denominator of the sum. We can use this method by writing a standard arithmetic expression involving fractions, assigning the result of the addition, and then printing our result.
Exploration 1.12.8. Adding an addition method.
(a) C++ Implementation.
Fraction operator +(const Fraction &otherFrac){
//Note the return type is a Fraction
int newnum = num*otherFrac.den + den*otherFrac.num;
int newden = den*otherFrac.den;
return Fraction(newnum, newden);
}
(b) Python Implementation.
def __add__(self, otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
return Fraction(newnum,newden)
(c) C++ Usage Example.
(d) Python Usage Example.
The addition method works as we desire, but a couple of things can be improved. When we use a binary operator like
+, we like more symmetry. Binary operators can either be members of their left-hand argument’s class or friend functions. Since the stream operators’ left-hand argument is a stream, stream operators (such as << and >>) must be either member functions of the stream class or friend functions of the class they are used with. However, that is not true for the + operator. Let’s rewrite the addition operator as a friend function.
Exploration 1.12.9. Overloading Addition.
(a) C++ Implementation.
Fraction operator +(const Fraction &frac1, const Fraction &frac2) {
int newnum = frac1.num * frac2.den + frac1.den * frac2.num;
int newden = frac1.den * frac2.den;
return Fraction(newnum, newden);
}
(b) Python Implementation.
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
return Fraction(newnum,newden)
(c) C++ Usage.
How you choose to overload operators like
+ is a design choice since both methods will work perfectly well. This is another example of encapsulation; your user does not need to know which you choose to use!
There is one more thing we can improve in our addition function. Note that \(6/8\) is the correct result (\(\frac {1}{4} + \frac {1}{2}\)) but that it is not in the “lowest terms” representation. The best representation would be \(3/4\text{.}\) In order to be sure that our results are always in the lowest terms, we need a helper function that knows how to reduce fractions. This function will need to look for the greatest common divisor, or GCD. We can then divide the numerator and the denominator by the GCD and the result will be reduced to lowest terms.
The best-known algorithm for finding a greatest common divisor is Euclid’s Algorithm, which will be discussed in detail in Chapter 8. Euclid’s Algorithm states that the greatest common divisor of two integers \(m\) and \(n\) is \(n\) if \(n\) divides \(m\) evenly. However, if \(n\) does not divide \(m\) evenly, then the answer is the greatest common divisor of \(n\) and the remainder of \(m\) divided by \(n\text{.}\) We will simply provide an iterative implementation here (see Exploration 1.12.10). Note that this implementation of the GCD algorithm only works when the denominator is positive. This is acceptable for our fraction class because we have said that a negative fraction will be represented by a negative numerator.
Exploration 1.12.10. Greatest Common Divisor.
Now we can use this function to help reduce any fraction. To put a fraction in lowest terms, we will divide the numerator and the denominator by their greatest common divisor. So, for the fraction \(6/8\text{,}\) the greatest common divisor is 2. Dividing the top and the bottom by 2 creates a new fraction, \(3/4\) (see Listing 1.12.3).
gcd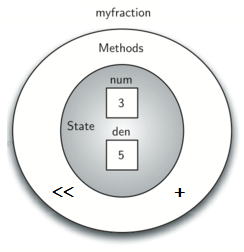
Visual representation of a Fraction class instance called ’myfraction’. It features concentric circles with the innermost labeled ’State’ showcasing ’num’ with a value of 3 above ’den’ with a value of 5, indicating the fraction’s numerator and denominator. The outer circle is labeled ’Methods’, suggesting the object’s functionality. Two symbols, ’<<’ and ’+’, are shown outside the Methods circle, implying additional methods.
Fraction Class with Two MethodsOur
Fraction object now has two very useful methods and looks like Figure 1.12.4. An additional group of methods that we need to include in our example Fraction class will allow two fractions to compare themselves to one another using ==.
We want the
== operator to compare Fraction objects and to return true if they are equivalent in value, false otherwise. This is a design choice because we want \(\frac {1}{2}\) to be considered equal to \(\frac {2}{4}\) as well as \(\frac {3}{6}\text{,}\) etc. Hence, in the Fraction class, we can implement the == method by cross-multiplying (see Task 1.12.11.a) rather than by just comparing numerators and denominators.
Of course there are other relational operators that can be overridden. For example, the
<= operator could be overridden to provide the less than or equal functionality.
Exploration 1.12.11. Overloading the comparison operator.
The complete
Fraction class, up to this point, is shown in Task 1.12.12.a. We leave the remaining arithmetic and relational methods as exercises.
Exploration 1.12.12. Complete Fraction class.
Subsection 1.12.4 Self-Check
To make sure you understand how operators are implemented in C++ classes, and how to properly write methods, write some methods to implement
*, /, and -. Also implement comparison operators > and <.
Our the next section will introduce another important aspect of object-oriented programming, namely inheritance.
Reading Questions Reading Questions
1.
2.
3.
4.
You have attempted of activities on this page.
