Value-Returning functions

Section 21.4 Value-Returning functions

Now let’s consider a more complicated situation—a recursive function that returns a value.

Many mathematical functions are defined recursively, because that is often the simplest way. For example, the factorial of an integer \(n\text{,}\) which is written \(n!\text{,}\) is defined like this:

\begin{align*} 0! = \amp 1\\ n! = \amp n \cdot(n-1)! \end{align*}

🔗

Don’t confuse the mathematical symbol \(!\text{,}\) which means factorial, with the C++ operator !, which means not. This definition says that factorial(0) is 1, and factorial(n) is n * factorial(n - 1).

🔗

It is trivial to turn that into a recursive function. The two parts of the definition are the base case and the recursive case:

🔗

Listing 21.4.1.

🔗

Why is the answer 120? Well...

factorial(5) is 5 * factorial(4)

🔗
factorial(4) is 4 * factorial(3)

🔗
factorial(3) is 3 * factorial(2)

🔗
factorial(2) is 2 * factorial(1)

🔗
factorial(1) is 1 * factorial(0)

🔗
factorial(0) is 1

🔗

🔗

If we use those rules to keep expanding `factorial(5) it looks like:

factorial(5)

🔗
(5 * factorial(4))

🔗
(5 * (4 * factorial(3)))

🔗
(5 * (4 * (3 * factorial(2))))

🔗
(5 * (4 * (3 * (2 * factorial(1)))))

🔗
(5 * (4 * (3 * (2 * (1 * factorial(0))))))

🔗
(5 * (4 * (3 * (2 * (1 * (1))))))

🔗

Once we there are no more factorial calls, we can evaluate the expression and get 120.

🔗

To actually see this play out in the code, it can help to break up the steps of the recursive case. This version of factorial does the same math, but prints more information along the way.

🔗

Listing 21.4.2.

🔗

Notice that as you run the code, you get a chance to see the values being returned at each step of the recursion.

🔗

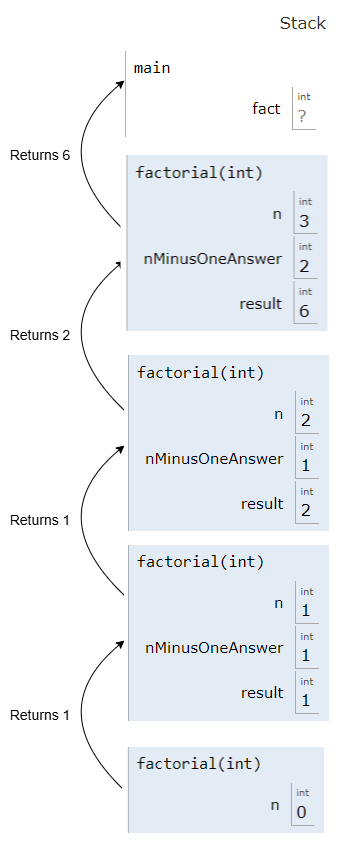
Insight 21.4.1.

It is easier to debug recursion if we store the value that is returned from the recursive call, calculate and store the answer for the current call, and then return the result. That way we can use a debugger or print statements to view how the result is being built up level by level.

🔗

The original version of factorial, which did return n * factorial(n - 1);, gave us no chance to see what came back from the call factorial(n - 1) or what value would be returned.

🔗

Below is a stack diagram that shows how the value is built up over the recursive calls. This stack diagram cheats a little. Instead of showing the stack at a particular point in time, it shows the final state of each stack frame all at the same time. It also shows what is being returned from one level to the next.

🔗

There are 4 stack frame boxes for the countdown function. They have different values of n, from 3 to 0. — Figure 21.4.3. Stack diagram for the `factorial` program.
🔗

Checkpoint 21.4.1.

Construct the function sumFrom(int start, int end). It should return the sum of all integers from start to end (inclusive). If start is greater than end, it should return 0.

🔗

Each call will be responsible for the current start value. Recursion will change the start.

🔗

int sumFrom(int start, int end) {
---
 #paired
---
    if (start > end) {
---
    if (start == end) { #paired
---
    if (start == 0) { #paired
---
        return 0;
    } else {
---
        return end;
    } else { #paired
---
        int rest = sumFrom(start + 1, end - 1);
---
        int rest = sumFrom(start, end); #paired
---
        int result = start + rest;
---
        int result = end + rest; #paired
---
        return result;
    }
---
        return rest;
    } #paired
---
}

🔗

Checkpoint 21.4.2.

Build another version of the function sumFrom(int start, int end). It should return the sum of all integers from start to end (inclusive). If start is greater than end, it should return 0.

🔗

This version will have two base cases. One for when start is equal to end, and another for when start is greater than end.

🔗

Each call should be responsible for the current end value. Recursion will change the end.

🔗

int sumFrom(int start, int end) {
---
 #paired
---
    if (start == end) {
        return end;
    }
---
    if (start == end) {
        return 0;
    } #paired
---
    else if (start > end) {
        return 0;
    }
---
    else if (start > end) {
        return end;
    } #paired
---
    else {
        int rest = sumFrom(start, end - 1);
---
    else {
        int rest = sumFrom(start + 1, end); #paired
---
    else {
        int rest = sumFrom(start + 1, end - 1); #paired
---
        int result = end + rest;
---
        int result = start + rest; #paired
---
        return result;
    }
---
        return rest;
    } #paired
---
}

🔗

You have attempted of activities on this page.

🔗

Prev Top Next