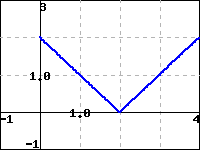
1.
Which is a parametric equation for the curve \(81 = \left(x+7\right)^{2}+\left(y-5\right)^{2}\text{?}\)
-
\(\displaystyle c(t) = \left(81\cos\mathopen{}\left(t\right)-7,5+81\sin\mathopen{}\left(t\right)\right)\)
-
\(\displaystyle c(t) = \left(5+9\cos\mathopen{}\left(t\right),9\sin\mathopen{}\left(t\right)-7\right)\)
-
\(\displaystyle c(t) = \left(9\cos\mathopen{}\left(t\right)-7,5+9\sin\mathopen{}\left(t\right)\right)\)
-
\(\displaystyle c(t) = \left(5+81\cos\mathopen{}\left(t\right),81\sin\mathopen{}\left(t\right)-7\right)\)