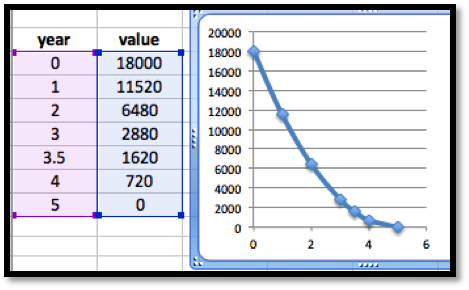
Example 7.7.1. Accumulating a constant function over time.
Mary runs a small shop that is temporarily disconnected from the power network. A generator that provides power uses 2 gallons of fuel per hour. How much fuel does she need to keep the shop running from 8 in the morning until 6 in the afternoon.
Solution.
We started with a problem that is easy to do without calculus to give us confidence in our method. We solve it with algebra first. Mary wants to run the generator for 10 hours and it consumes 2 gallons of fuel per hour. She needs (10 hours)(2 gallons/hour) = 20 gallons of fuel.
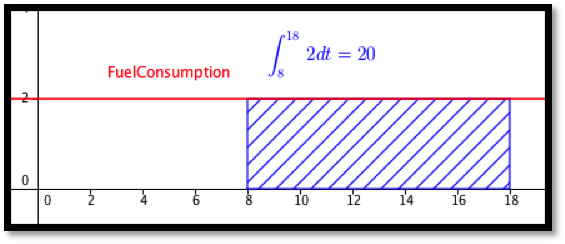
To set the problem up for calculus, we use a 24-hour clock to put time on a number line. We are accumulating \(\text{FuelConsumption}(t)=2\) from \(t=8\) to \(t=18\text{.}\) We need
\begin{equation*}
\int_8^{18} 2 dt=2t|_8^{18}=(2*18)-(2*8)=20\text{.}
\end{equation*}
gallons of fuel.