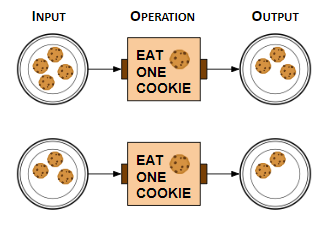
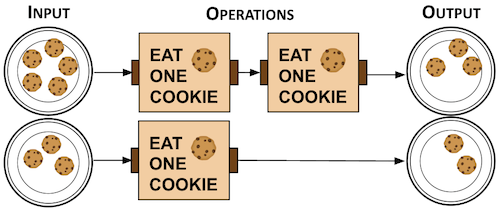
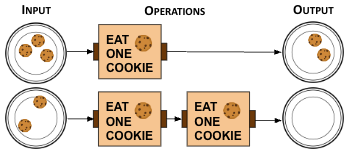
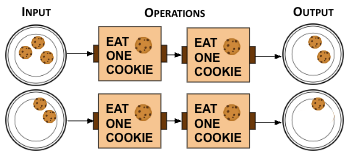
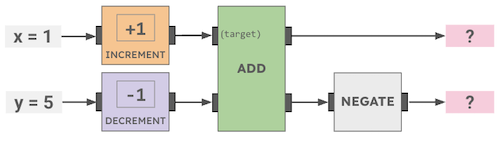
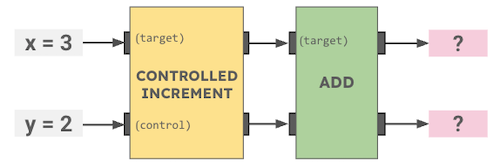
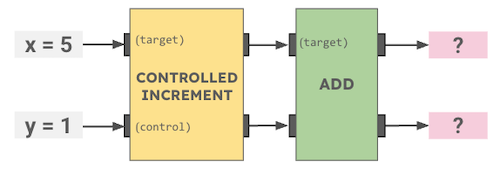
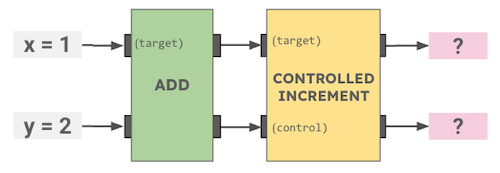
- 0 cookies
- There were only two "eat cookie" operations.
- 1 cookie
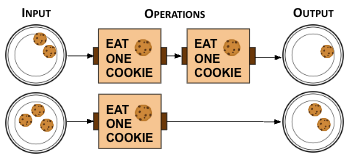
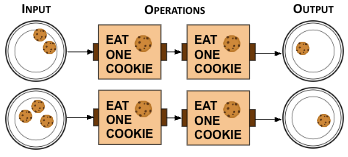
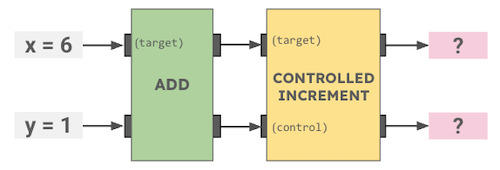
- Yes! Start with 3 cookies, eat 2 cookies, and you are left with 1 cookie.
- 2 cookies
- There were two "eat cookie" operations.
- 3 cookies
- You need to apply the "eat cookies" operations.
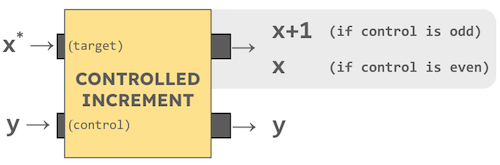
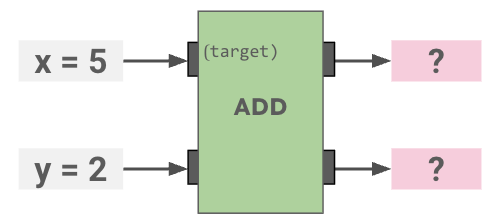
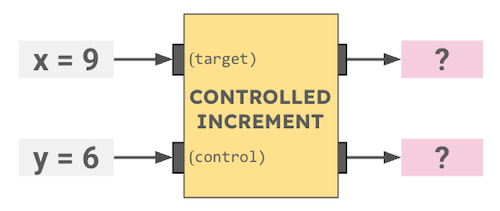
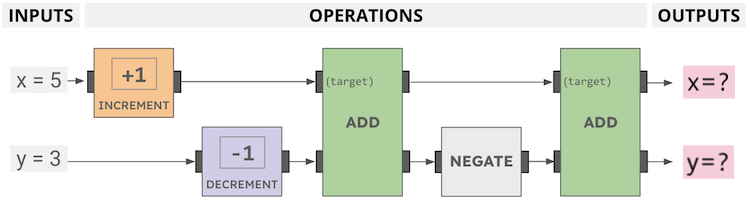
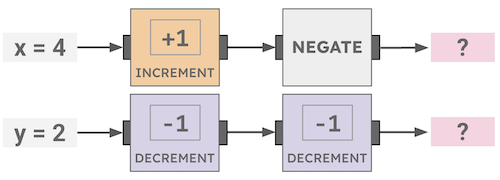
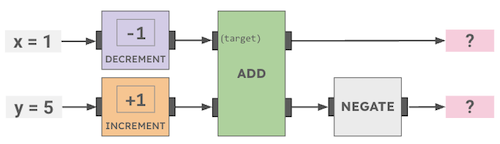
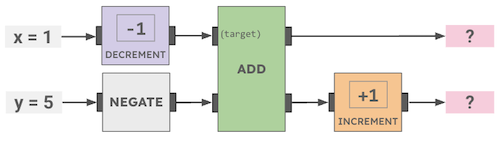
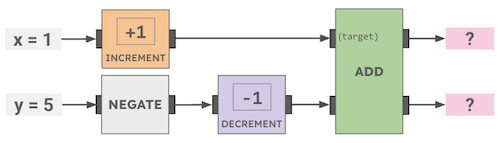
How many cookies will be left after this Cookie Circuit runs?
Hint.
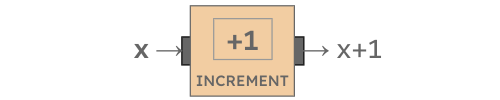
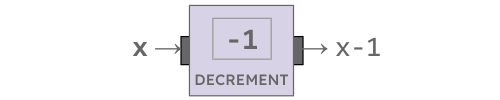
Operations are read left to right