6.5. Representación de lista de listas¶
En un árbol representado por una lista de listas, comenzaremos con la estructura de datos de las listas de Python y escribiremos las funciones definidas anteriormente. Aunque escribir la interfaz como un conjunto de operaciones sobre una lista es un poco diferente de los otros tipos abstractos de datos que hemos implementado, es interesante hacerlo porque nos proporciona una estructura de datos recursiva simple que podemos mirar y examinar directamente . En un árbol representado como una lista de listas, almacenaremos el valor del nodo raíz como el primer elemento de la lista. El segundo elemento de la lista será en sí mismo una lista que represente el subárbol izquierdo. El tercer elemento de la lista será otra lista que represente el subárbol derecho. Veamos un ejemplo para ilustrar esta técnica de almacenamiento. La Figura 1 muestra un árbol simple y su correspondiente implementación como una lista.
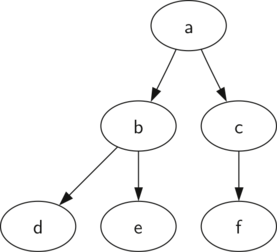
Figura 1: Un pequeño árbol¶
Figura 1: Un pequeño árbol
miArbol = ['a', #raíz
['b', #subárbol izquierdo
['d', [], []],
['e', [], []] ],
['c', #subárbol derecho
['f', [], []],
[] ]
]
Note que podemos acceder a los subárboles de la lista mediante la indización estándar para listas. La raíz del árbol es miArbol[0], el subárbol izquierdo de la raíz es miArbol[1], y el subárbol derecho es miArbol[2]. El ActiveCode 1 ilustra la creación de un árbol simple usando una lista. Una vez construido el árbol, podemos acceder a la raíz y a los subárboles izquierdo y derecho. Una propiedad muy conveniente de este enfoque de lista de listas es que la estructura de una lista que representa un subárbol se ajusta a la estructura definida para un árbol; ¡la estructura en sí misma es recursiva! Un subárbol que tiene un valor raíz y dos listas vacías es un nodo hoja. Otra buena característica del enfoque de lista de listas es que es generalizable a un árbol que tiene muchos subárboles. En caso que el árbol sea mayor que un árbol binario, otro subárbol será simplemente otra lista.
Formalicemos esta definición de la estructura de datos árbol proporcionando algunas funciones que nos faciliten usar las listas como árboles. Tenga en cuenta que no vamos a definir una clase Arbol Binario. Las funciones que escribiremos solo nos ayudarán a manipular una lista estándar como si estuviéramos trabajando con un árbol.
def ArbolBinario(r):
return [r, [], []]
La función ArbolBinario simplemente construye una lista con un nodo raíz y dos sublistas vacías para los hijos. Para agregar un subárbol izquierdo a la raíz de un árbol, necesitamos insertar una nueva lista en la segunda posición de la lista raíz. Debemos ser cuidadosos. Si la lista ya tiene algún contenido en la segunda posición, necesitamos rastrearlo y empujarlo hacia abajo en el árbol para que sea el hijo izquierdo de la lista que estamos agregando. El Programa 1 muestra el código en Python para insertar un hijo izquierdo.
Programa 1
def insertarIzquierdo(raiz,nuevaRama):
t = raiz.pop(1)
if len(t) > 1:
raiz.insert(1,[nuevaRama,t,[]])
else:
raiz.insert(1,[nuevaRama, [], []])
return raiz
Note que para insertar un hijo izquierdo, primero obtendremos la lista (posiblemente vacía) que corresponde al hijo izquierdo actual. A continuación, agregamos el nuevo hijo izquierdo, instalando el antiguo hijo izquierdo como hijo izquierdo del nuevo. Esto nos permite empalmar un nuevo nodo en el árbol en cualquier posición. El código de insertarDerecho es similar al de inserttarIzquierdo y se muestra en el Programa 2.
Programa 2
def insertarDerecho(raiz,nuevaRama):
t = raiz.pop(2)
if len(t) > 1:
raiz.insert(2,[nuevaRama,[],t])
else:
raiz.insert(2,[nuevaRama,[],[]])
return raiz
Para redondear este conjunto de funciones de creación de árboles (ver el Programa 3), vamos a escribir un par de funciones de acceso para obtener y establecer el valor raíz, así como para obtener los subárboles izquierdo o derecho.
Programa 3
def obtenerValorRaiz(raiz):
return raiz[0]
def asignarValorRaiz(raiz,nuevoValor):
raiz[0] = nuevoValor
def obtenerHijoIzquierdo(raiz):
return raiz[1]
def obtenerHijoDerecho(raiz):
return raiz[2]
El ActiveCode 2 ejecuta las funciones que acabamos de escribir para árboles. Usted debe probarlo por sí mismo. Uno de los ejercicios le pide que dibuje la estructura de árbol resultante de este conjunto de llamadas.
Autoevaluación
- ['a', ['b', [], []], ['c', [], ['d', [], []]]]
- No es así, este árbol no tiene el nodo 'e'.
- ['a', ['c', [], ['d', ['e', [], []], []]], ['b', [], []]]
- Esto está cerca, pero si usted mira cuidadosamente verá que los hijos izquierdo y derecho de la raíz están intercambiados.
- ['a', ['b', [], []], ['c', [], ['d', ['e', [], []], []]]]
- Muy bien
- ['a', ['b', [], ['d', ['e', [], []], []]], ['c', [], []]]
- Esto está cerca, pero los nombres de los hijos izquierdo y derecho han sido intercambiados junto con las estructuras subyacentes.
Q-3: Dadas las siguientes instrucciones:
x = ArbolBinario('a')
insertarIzquierdo(x,'b')
insertarDerecho(x,'c')
insertarDerecho(obtenerHijoDerecho(x),'d')
insertarIzquierdo(obtenerHijoDerecho(obtenerHijoDerecho(x)),'e')
¿Cuál de las siguientes respuestas corresponde a la representación correcta del árbol?
Escriba una función crearArbol que devuelva un árbol usando las funciones de lista de listas y que corresponda al siguiente árbol: