6.16. Árboles binarios de búsqueda equilibrados¶
En la sección anterior estudiamos la construcción de un árbol binario de búsqueda. Como aprendimos, el desempeño del árbol binario de búsqueda puede degradarse a \(O(n)\) para operaciones como obtener y agregar cuando el árbol se desequilibra. En esta sección examinaremos un tipo especial de árbol binario de búsqueda que garantiza automáticamente que el árbol permanezca equilibrado en todo momento. Este árbol se llama un árbol AVL en razón a sus inventores: G.M. Adelson-Velskii y E.M. Landis.
Un árbol AVL implementa el tipo abstracto de datos Vector Asociativo al igual que un árbol binario de búsqueda regular, la única diferencia está en cómo el árbol se desempeña. Para implementar nuestro árbol AVL necesitamos hacer seguimiento de un factor de equilibrio para cada nodo en el árbol. Hacemos esto observando las alturas de los subárboles izquierdo y derecho para cada nodo. Más formalmente, definimos el factor de equilibrio para un nodo como la diferencia entre la altura del subárbol izquierdo y la altura del subárbol derecho.
Utilizando la definición de factor de equilibrio dada anteriormente, decimos que un subárbol es pesado a la izquierda si el factor de equilibrio es mayor que cero. Si el factor de equilibrio es menor que cero, entonces el subárbol es pesado a la derecha. Si el factor de equilibrio es cero entonces el árbol está perfectamente equilibrado. Para propósitos de implementar un árbol AVL y obtener el beneficio de tener un árbol equilibrado, definiremos que un árbol estará en equilibrio si el factor de equilibrio es -1, 0 ó 1. Una vez que el factor de equilibrio de un nodo en un árbol esté fuera de este rango necesitaremos un procedimiento para reequilibrar el árbol nuevamente. La Figura 1 muestra un ejemplo de un árbol desequilibrado y pesado a la derecha y los factores de equilibrio de cada nodo.
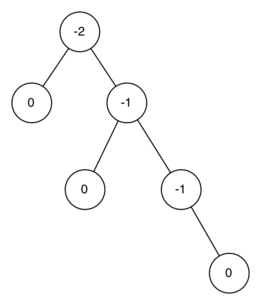
Figura 1: Un árbol desequilibrado y pesado a la derecha con factores de equilibrio¶
Figura 1: Un árbol desequilibrado y pesado a la derecha con factores de equilibrio