7.4. Una matriz de adyacencia

Una de las maneras más fáciles de implementar un grafo es usar una matriz bidimensional. En esta implementación de matriz, cada una de las filas y columnas representa un vértice en el grafo. El valor que se almacena en la celda en la intersección de la fila $v$ y la columna $w$ indica si hay una arista desde el vértice $v$ al vértice $w$. Cuando dos vértices están conectados por una arista, decimos que son adyacentes. La Figura 3 ilustra la matriz de adyacencia para el grafo de la Figura 2. Un valor en una celda representa la ponderación de la arista que une el vértice $v$ con el vértice $w$.

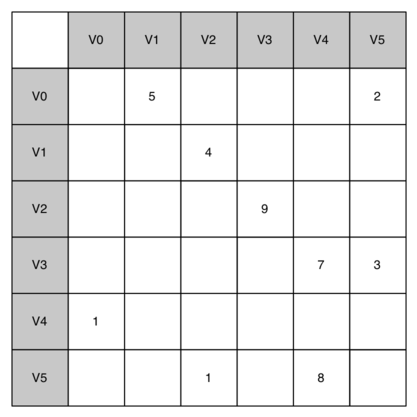
Figura 3: Una representación de un grafo mediante una matriz de adyacencia

Figura 3: Una representación de un grafo mediante una matriz de adyacencia

La ventaja de la matriz de adyacencia es que es simple, y que para grafos pequeños es fácil ver qué nodos están conectados a otros nodos. Sin embargo, note que la mayoría de las celdas de la matriz están vacías. Dado que la mayoría de las celdas están vacías decimos que esta matriz es “rala”. Una matriz no es una forma muy eficiente de almacenar datos ralos. De hecho, en Python usted debe incluso esforzarse por crear una estructura de matriz como la de la Figura 3.

La matriz de adyacencia es una buena implementación para un grafo cuando el número de aristas es grande. Pero ¿qué entendemos por grande? ¿Cuántas aristas se necesitarían para llenar la matriz? Puesto que hay una fila y una columna para cada vértice en el grafo, el número de aristas requeridas para llenar la matriz es $|V{|}^2$. Una matriz está llena cuando cada vértice está conectado a todos los otros vértices. Hay pocos problemas reales que se aproximan a este tipo de conectividad. Los problemas que veremos en este capítulo se refieren a grafos que están conectados de forma rala.

You have attempted 1 of 1 activities on this page