7.14. Análisis de la gira del caballo

Hay un último tema interesante sobre el problema de la gira del caballo, luego pasaremos a la versión general de la búsqueda en profundidad. El tema es el desempeño. En particular, giraCaballo es muy sensible al método que usted use para seleccionar el siguiente vértice a visitar. Por ejemplo, en un tablero de cinco por cinco usted puede producir una ruta en aproximadamente 1.5 segundos en una computadora razonablemente rápida. Pero, ¿qué ocurre si usted intenta hacerlo con un tablero de ocho por ocho? En este caso, dependiendo de la velocidad de su computadora, ¡usted podría tener que esperar hasta media hora para obtener los resultados! La razón de esto es que el problema de la gira del caballo, como lo hemos implementado hasta ahora, es un algoritmo exponencial de tamaño $O(k^N)$, donde N es el número de cuadrados en el tablero de ajedrez, y k es una constante pequeña. La Figura 12 puede ayudarnos a visualizar por qué esto es así. La raíz del árbol representa el punto de partida de la búsqueda. A partir de ahí el algoritmo genera y comprueba cada uno de los movimientos posibles que el caballo puede hacer. Como hemos notado antes, el número de movimientos posibles depende de la posición del caballo en el tablero. En las esquinas hay sólo dos movimientos legales, en los cuadrados adyacentes a las esquinas hay tres y en el centro del tablero hay ocho. La Figura 13 muestra el número de movimientos posibles para cada posición en un tablero. En el siguiente nivel del árbol hay otra vez entre 2 y 8 movimientos siguientes posibles desde la posición que estamos explorando actualmente. El número de posiciones posibles por examinar corresponde al número de nodos en el árbol de búsqueda.

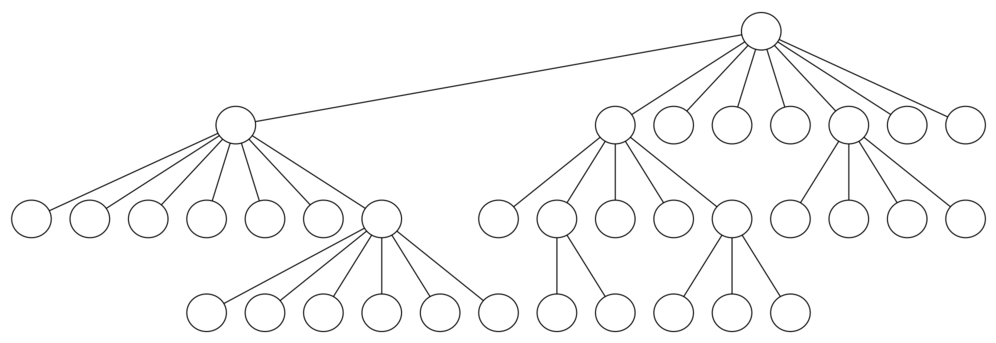
Figura 12: Un árbol de búsqueda para la gira del caballo

Figura 12: Un árbol de búsqueda para la gira del caballo

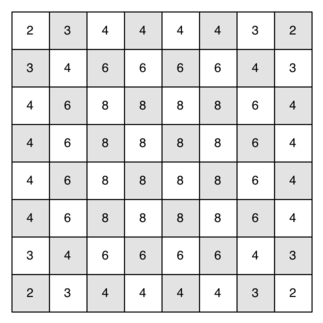
Figura 13: Número de movimientos posibles para cada cuadrado

Figura 13: Número de movimientos posibles para cada cuadrado

Ya hemos visto que el número de nodos en un árbol binario de altura N es $2^{N+1}-1$. Para un árbol con nodos que pueden tener hasta ocho hijos en lugar de dos, el número de nodos es mucho mayor. Debido a que el factor de ramificación de cada nodo es variable, podríamos estimar el número de nodos usando un factor de ramificación promedio. Lo importante a destacar es que este algoritmo es exponencial: $k^{N+1}-1$, donde $k$ es el factor de ramificación promedio para el tablero. ¡Veamos cuán rápidamente crece esto! Para un tablero de tamaño 5x5, el árbol será de 25 niveles de profundidad, o N = 24 contando el primer nivel como nivel 0. El factor de ramificación promedio es $k=3.8$; así que el número de nodos en el árbol de búsqueda es ${3.8}^{25}-1$ ó $3.12\times {10}^{14}$. Para un tablero de tamaño 6x6, $k=4.4$, hay $1.5\times {10}^{23}$ nodos, y para un tablero de ajedrez regular de 8x8, $k=5.25$, hay $1.3\times {10}^{46}$. Por supuesto, dado que existen múltiples soluciones al problema, no tendremos que explorar cada uno de los nodos, pero la parte fraccional de los nodos que tenemos que explorar es simplemente un multiplicador constante que no cambia la naturaleza exponencial del problema. Dejaremos que usted vea, como ejercicio, si puede expresar $k$ en función del tamaño del tablero.

Por suerte hay una manera de acelerar el caso de un tablero ocho por ocho para que funcione en menos de un segundo. En el programa siguiente mostramos el código que acelera giraCaballo. Esta función (ver el Programa 4), llamada ordenPorDisp se utilizará en lugar de la llamada a u.obtenerConexiones en el código mostrado anteriormente. La línea crítica en la función ordenPorDisp es la línea 10. Esta línea asegura que seleccionemos, para ir a continuación, el vértice que tenga el menor número de movimientos disponibles. Usted podría pensar que esto es realmente contraproducente; ¿por qué no seleccionar el nodo que tiene la mayor cantidad de movimientos disponibles? Usted puede probar ese enfoque fácilmente ejecutando el programa usted mismo e insertando la línea listaRes.reverse() justo después del ordenamiento.

El problema de usar el vértice con la mayor cantidad de movimientos disponibles como siguiente vértice en la ruta es que tiende a que el caballo tenga que visitar los cuadrados del medio anticipadamente durante la gira. Cuando esto sucede, es factible que el caballo se quede varado en un lado del tablero donde no puede alcanzar cuadrados no visitados en el otro lado del tablero. Por otro lado, visitar primero los cuadrados con el menor número de movimientos disponibles obliga al caballo a visitar primero los cuadrados alrededor de los bordes del tablero. Esto asegura que el caballo visite temprano las esquinas difíciles de alcanzar y pueda usar los cuadrados del medio para saltar a través del tablero solamente cuando sea necesario. Utilizar este tipo de conocimiento para acelerar un algoritmo se denomina heurística. Los seres humanos usan la heurística todos los días para ayudar a tomar decisiones, las búsquedas heurísticas se utilizan a menudo en el campo de la inteligencia artificial. Esta heurística particular se llama el algoritmo de Warnsdorff, nombrado en honor a H. C. Warnsdorff que publicó su idea en 1823.

Programa 4

def ordenPorDisp(n):
    listaRes = []
    for v in n.obtenerConexiones():
        if v.obtenerColor() == 'blanco':
            c = 0
            for w in v.obtenerConexiones():
                if w.obtenerColor() == 'blanco':
                    c = c + 1
            listaRes.append((c,v))
    listaRes.sort(key=lambda x: x[0])
    return [y[1] for y in listaRes]

You have attempted 1 of 1 activities on this page