Note 6.2.1.
The names of the variables have been chosen to help readability.
Section 6.2 The while Statement
There is another Python statement that can also be used to build an iteration. It is called the
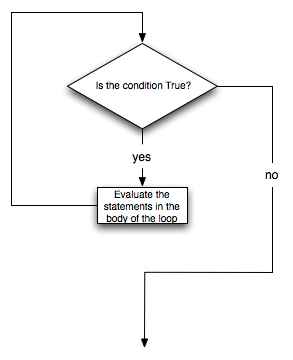
while statement. The while statement provides a much more general mechanism for iterating. Similar to the if statement, it uses a boolean expression to control the flow of execution. The body of while will be repeated as long as the controlling boolean expression evaluates to True.
The following two figures show the flow of control. The first focuses on the flow inside the while loop and the second shows the while loop in context.
We can use the
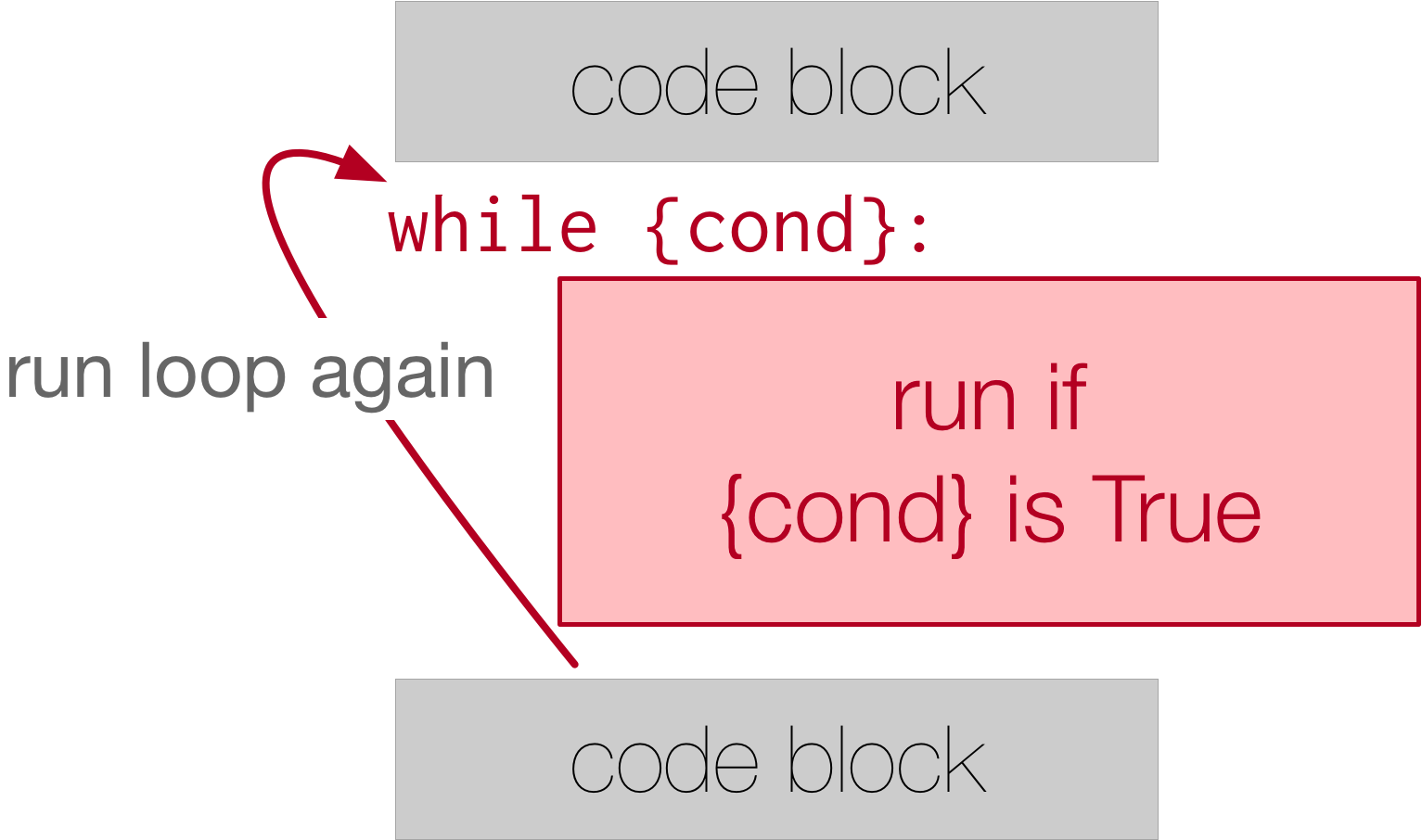
while loop to create any type of iteration we wish, including anything that we have previously done with a for loop. For example, the program in the previous section could be rewritten using while. Instead of relying on the range function to produce the numbers for our summation, we will need to produce them ourselves. To do this, we will create a variable called aNumber and initialize it to 1, the first number in the summation. Every iteration will add aNumber to the running total until all the values have been used. In order to control the iteration, we must create a boolean expression that evaluates to True as long as we want to keep adding values to our running total. In this case, as long as aNumber is less than or equal to the bound, we should keep going.
Here is a new version of the summation program that uses a while statement.
You can almost read the
while statement as if it were in natural language. It means, while aNumber is less than or equal to aBound, continue executing the body of the loop. Within the body, each time, update theSum using the accumulator pattern and increment aNumber. After the body of the loop, we go back up to the condition of the while and reevaluate it. When aNumber becomes greater than aBound, the condition fails and flow of control continues to the return statement.
The same program in codelens will allow you to observe the flow of execution.
More formally, here is the flow of execution for a
while statement:
-
If the condition is
True, execute each of the statements in the body and then go back to step 1.
The body consists of all of the statements below the header with the same indentation.
This type of flow is called a loop because the third step loops back around to the top. Notice that if the condition is
False the first time through the loop, the statements inside the loop are never executed.
The body of the loop should change the value of one or more variables so that eventually the condition becomes
False and the loop terminates. Otherwise the loop will repeat forever. This is called an infinite loop. An endless source of amusement for computer scientists is the observation that the directions written on the back of the shampoo bottle (lather, rinse, repeat) create an infinite loop.
In the case shown above, we can prove that the loop terminates because we know that the value of
aBound is finite, and we can see that the value of aNumber increments each time through the loop, so eventually it will have to exceed aBound. In other cases, it is not so easy to tell.
Note 6.2.2.
Introduction of the while statement causes us to think about the types of iteration we have seen. The
for statement will always iterate through a sequence of values like the list of names for the party or the list of numbers created by range. Since we know that it will iterate once for each value in the collection, it is often said that a for loop creates a definite iteration because we definitely know how many times we are going to iterate. On the other hand, the while statement is dependent on a condition that needs to evaluate to False in order for the loop to terminate. Since we do not necessarily know when this will happen, it creates what we call indefinite iteration. Indefinite iteration simply means that we don’t know how many times we will repeat but eventually the condition controlling the iteration will fail and the iteration will stop. (Unless we have an infinite loop which is of course a problem)
What you will notice here is that the
while loop is more work for you — the programmer — than the equivalent for loop. When using a while loop you have to control the loop variable yourself. You give it an initial value, test for completion, and then make sure you change something in the body so that the loop terminates. That also makes a while loop harder to read and understand than the equivalent for loop. So, while you can implement definite iteration with a while loop, it’s not a good idea to do that. Use a for loop whenever it will be known at the beginning of the iteration process how many times the block of code needs to be executed.
Check your understanding
Checkpoint 6.2.3.
The following code contains an infinite loop. Which is the best explanation for why the loop does not terminate?
n = 10
answer = 1
while ( n > 0 ):
answer = answer + n
n = n + 1
print(answer)
- n starts at 10 and is incremented by 1 each time through the loop, so it will always be positive
- The loop will run as long as n is positive. In this case, we can see that n will never become non-positive.
- answer starts at 1 and is incremented by n each time, so it will always be positive
- While it is true that answer will always be positive, answer is not considered in the loop condition.
- You cannot compare n to 0 in while loop. You must compare it to another variable.
- It is perfectly valid to compare n to 0. Though indirectly, this is what causes the infinite loop.
- In the while loop body, we must set n to False, and this code does not do that.
- The loop condition must become False for the loop to terminate, but n by itself is not the condition in this case.
Checkpoint 6.2.4.
Write a while loop that is initialized at 0 and stops at 15. If the counter is an even number, add double its value to
total_score. If the counter is an odd number, subtract half its value from total_score.
Checkpoint 6.2.5.
Write a function called
stop_at_one that takes an integer as a parameter, and performes the following operations on it until the integer equals 1: If the number is odd, multiply by 3 and add 1. If the number is even, divide by two. The function should then return how many iterations it took to reach 1.
You have attempted of activities on this page.
