Problems and Definitions

Section 2.1 Problems and Definitions

Objectives

After completing this section, you should be able to do the following.

Use the language of graph theory to describe properties of graphs.
Utilize multiple representations of graphs.
Apply the Handshake Lemma to answer questions about graphs and problems they represent.

Subsection Section Preview

Investigate!

In the time of Euler, in the town of Königsberg in Prussia, there was a river containing two islands. The islands were connected to the banks of the river by seven bridges (as seen below). The bridges were very beautiful, and on their days off, townspeople would spend time walking over the bridges. As time passed, a question arose: Was it possible to plan a walk so that you cross each bridge once and only once? Euler was able to answer this question. Are you?

🔗

$Drawing of a river (blue) running left to right with two islands. There are 7 bridges over the river: two from the top bank to the left island, two from the left island to the bottom bank, and a bridge from the right island to each of the top bank, bottom bank, and left island.$

🔗

Graph Theory is a relatively new area of mathematics, first studied by the super famous mathematician Leonhard Euler in 1735. Since then it has blossomed into a powerful tool used in nearly every branch of science and is currently an active area of mathematics research.

🔗

The problem above, known as the Seven Bridges of Königsberg, is the problem that originally inspired graph theory. Consider a “different” problem: Below is a drawing of four dots connected by some lines. Is it possible to trace over each line once and only once (without lifting your pencil, starting and ending on a dot)?

🔗

$Three dots aligned in a vertical column left of a single dot on the right. Lines connect the dot on the right to each dot on the left. Among the dots on the left, two arced lines connect the bottom dot to the center dot, and two more connect the center dot to the top dot.$

There is an obvious connection between these two problems. Any path in the dot and line drawing corresponds exactly to a path over the bridges of Königsberg.

🔗

Pictures like this dot and line drawing are called graphs (although technically, the picture above is a multigraph). Graphs are made up of a collection of dots called vertices and lines connecting those dots called edges. When two vertices are connected by an edge, we say they are adjacent. The nice thing about looking at graphs instead of pictures of rivers, islands, and bridges is that we now have a mathematical object to study. We have distilled the “important” parts of the bridge picture for the problem. It does not matter how big the islands are, what the bridges are made out of, if the river contains alligators, etc. All that matters is which land masses are connected to which other land masses, and how many times. This was the great insight Euler had.

🔗

We will return to the question of finding paths through graphs in Section 2.4. In this section, we will explore various ways that graphs can be used to represent, or model, real-world problems. Along the way, we will introduce some basic definitions, terminology, and notation that will be used in the rest of the chapter.

🔗

Worksheet Preview Activity
A4 US

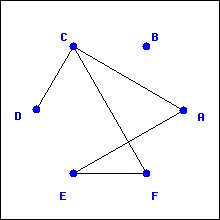
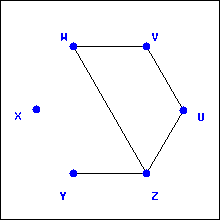
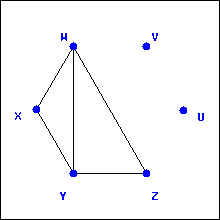
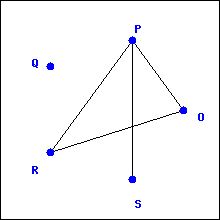
To get a feel for graphs and the types of questions we want to ask about them, let’s explore four examples of graphs.

🔗

G_{1} :

🔗

G_{2} :

🔗

$Petersen graph: ten vertices each with three edges. Five of the vertices form a 5-pointed star, the other five a pentagon, edges connecting the vertices of the star and the pentagon.$

$A graph with six vertices arranged in two rows of three. The top vertices are labeled v1, v2, v3 from left to right. The bottom vertices are labeled v6, v5, v4 from left to right. Three edges connect each vertex in the top row to the vertex below it. Four more edges connect vertices on the top row and along the bottom row in two X configurations.$

G_{3} :

🔗

G_{4} :

🔗

vertex	adjacent to
$a$	$b, c$
$b$	$a, f$
$c$	$a, d, e$
$d$	$c, e, f$
$e$	$c, d$
$f$	$b, d$

(\begin{matrix} 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \end{matrix})

🔗

The graph

G_{3}

is presented as an adjacency list where each vertex gets a list of which other vertices it is adjacent to. The graph

G_{4}

is presented as an adjacency matrix where the rows and columns correspond to the vertices and the entries are 1 if the vertices are adjacent and 0 otherwise. Before answering the questions below, it might be helpful to draw a more traditional representation of these graphs.

🔗

1.

First, let’s count the number of vertices and edges in each graph.

🔗

Number of vertices:

G_{1} :

;

G_{2} :

;

G_{3} :

;

G_{4} :

🔗

Number of edges:

G_{1} :

;

G_{2} :

;

G_{3} :

;

G_{4} :

🔗

2.

We call the number of edges incident to a particular vertex (i.e., the number of edges “coming out of” the vertex) the degree of the vertex. A list of the degrees of all the vertices in non-increasing order is called a degree sequence for the graph. Find the degree sequence for each graph.

🔗

G_{1}

has degree sequence: .

🔗

G_{2}

has degree sequence: .

🔗

G_{3}

has degree sequence: .

🔗

G_{4}

has degree sequence: .

🔗

3.

We often care about paths between vertices in a graph. A graph is connected if there is a path between every pair of vertices. Sometimes there is a path that starts at a vertex and eventually comes back to itself, which is called a cycle.

🔗

(a)

Which of the graphs are connected?

🔗

$G_{1}$
$G_{2}$
$G_{3}$
$G_{4}$
None of the above

🔗

(b)

Which of the graphs contain cycles?

🔗

$G_{1}$
$G_{2}$
$G_{3}$
$G_{4}$
None of the above

🔗

(c)

Graphs that are connected and contain no cycles are called trees. For each graph, how many edges must you remove to turn it into a tree? (If it is already a tree, the answer would be 0.)

🔗

G_{1} :

;

G_{2} :

;

G_{3} :

;

G_{4} :

🔗

4.

For which of the graphs is it possible to draw the graph in such a way that no edges cross?

🔗

$G_{4}$
$G_{1}$
$G_{3}$
$G_{2}$
None of the above

🔗

5.

Suppose we color each vertex of a graph so that adjacent vertices always have different colors. The smallest number of colors needed to do this is called the chromatic number of the graph. Find the chromatic number for each graph.

🔗

G_{1} :

;

G_{2} :

;

G_{3} :

;

G_{4} :

🔗

Note: If the graphs represented friendships between people, then the chromatic number would tell us the minimum number of groups we would need if we wanted to divide up everyone into groups of people who were not yet friends.

🔗

Subsection What is a Graph?

Before we start studying graphs, we need to agree upon what a graph is. While we almost always think of graphs as pictures (dots connected by lines), this is fairly ambiguous. Do the lines need to be straight? Does it matter how long the lines are or how large the dots are? Can there be two lines connecting the same pair of dots? Can one line connect three dots?

🔗

The way we avoid ambiguities in mathematics is to provide concrete and rigorous definitions. Crafting good definitions is not easy, but it is incredibly important. The definition is the agreed-upon starting point from which all truths in mathematics proceed. Is there a graph with no edges? We have to look at the definition to see if this is possible.

🔗

We want our definition to be precise and unambiguous, but it also must agree with our intuition for the objects we are studying. It needs to be useful: We could define a graph to be a six-legged mammal, but that would not let us solve any problems about bridges. Instead, here is the (now) standard definition of a graph.

🔗

Definition 2.1.1. Graph.

A graph is an ordered pair

G = (V, E)

consisting of a nonempty set

V

(called the vertices) and a set

E

(called the edges) of two-element subsets of

V .

🔗

Strange. Nowhere in the definition is there talk of dots or lines. From the definition, a graph could be

🔗

({a, b, c, d}, {{a, b}, {a, c}, {b, c}, {b, d}, {c, d}}) .

Here we have a graph with four vertices (the letters

a, b, c, d

) and five edges (the pairs

{a, b}, {a, c}, {b, c}, {b, d}, {c, d})

🔗

Looking at sets and sets of 2-element sets is difficult to process. That is why we often draw a representation of these sets. We put a dot down for each vertex, and connect two dots with a line precisely when those two vertices are one of the 2-element subsets in our set of edges. Thus one way to draw the graph described above is this:

🔗

$Four vertices arranged in a square, with edges on the border of the square and one connecting the bottom left vertex to the top right vertex. Vertices are labeled a (top left), b (top right), c (bottom left) and d (bottom right).$

However we could also have drawn the graph differently. For example either of these:

🔗

$Four vertices arranged in a square. Vertices are labeled a (top left), d (top right), c (bottom left) and b (bottom right). Edges connect a to c and b, d to b and c, and c to b.$

$Four vertices arranged in a horizontal row, labeled a, b, c, and d from left to right. Edges connect each vertex to the one on its right. A curved edge connects a to c, and another curved edge connects b to d.$

We should be careful about what it means for two graphs to be “the same.” Actually, given our definition, this is easy: Are the vertex sets equal? Are the edge sets equal? We know what it means for sets to be equal, and graphs are nothing but a pair of two special sorts of sets.

🔗

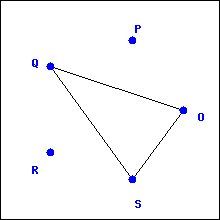
Example 2.1.2.

Are the graphs below equal?

🔗

G_{1} = ({a, b, c}, {{a, b}, {b, c}}); G_{2} = ({a, b, c}, {{a, c}, {c, b}}) .

🔗

Solution.

No. Here the vertex sets of each graph are equal, which is a good start. Also, both graphs have two edges. In the first graph, we have edges

{a, b}

and

{b, c},

while in the second graph we have edges

{a, c}

and

{c, b} .

Of course,

{b, c} = {c, b},

so that is not the problem. The issue is that

{a, b} \neq {a, c} .

Since the edge sets of the two graphs are not equal (as sets), the graphs are not equal (as graphs).

🔗

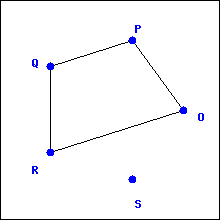
Even if two graphs are not equal, they might be basically the same. The graphs in the previous example could be drawn like this:

🔗

$Two graphs with three vertices each arranged in a horizontal row. Edges connect vertices to the vertex on either side of it. The graph on the left (G1) has vertices labeled a, b, c from left to right. The graph on the right (G2) has vertices labeled a, c, b from left to right.$

Graphs that are basically the same (but perhaps not equal) are called isomorphic. We will give a precise definition of this term after a quick example:

🔗

Example 2.1.3.

Consider the graphs:

🔗

G_{1} = (V_{1}, E_{1}) where V_{1} = {a, b, c} and E_{1} = {{a, b}, {a, c}, {b, c}};

G_{2} = (V_{2}, E_{2}) where V_{2} = {u, v, w} and E_{2} = {{u, v}, {u, w}, {v, w}} .

🔗

Are these graphs the same?

🔗

Solution.

The two graphs are NOT equal. It is enough to notice that

V_{1} \neq V_{2}

since

a \in V_{1}

but

a \notin V_{2} .

However, both of these graphs consist of three vertices with edges connecting every pair of vertices. We can draw them as follows:

$A graph with three vertices arranged as a triangle, with edges along the border of the triangle. The vertices are labeled a, b, and c.$

$A graph with three vertices arranged as a triangle, with edges along the border of the triangle. The vertices are labeled u, v, and w.$

Clearly we want to say these graphs are basically the same, so while they are not equal, they will be isomorphic. We can rename the vertices of one graph and get the second graph as the result.

🔗

Intuitively, graphs are isomorphic if they are basically the same, or better yet, if they are the same except for the names of the vertices. To make the concept of renaming vertices precise, we give the following definitions:

🔗

Definition 2.1.4.

An isomorphism between two graphs

G_{1}

and

G_{2}

is a bijection

f : V_{1} \to V_{2}

between the vertices of the graphs such that

{a, b}

is an edge in

G_{1}

if and only if

{f (a), f (b)}

is an edge in

G_{2} .

🔗

Two graphs are isomorphic if there is an isomorphism between them. In this case we write

G_{1} ≅ G_{2} .

🔗

An isomorphism is simply a function which renames the vertices. It must be a bijection so every vertex gets a new name. These newly named vertices must be connected by edges precisely when they were connected by edges with their old names.

🔗

Example 2.1.5.

Decide whether the graphs

G_{1} = (V_{1}, E_{1})

and

G_{2} = (V_{2}, E_{2})

are equal or isomorphic.

🔗

V_{1} = {a, b, c, d},

E_{1} = {{a, b}, {a, c}, {a, d}, {c, d}}

🔗

V_{2} = {a, b, c, d},

E_{2} = {{a, b}, {a, c}, {b, c}, {c, d}}

🔗

Solution.

The graphs are NOT equal, since

{a, d} \in E_{1}

but

{a, d} \notin E_{2} .

However, since both graphs contain the same number of vertices and the same number of edges, they might be isomorphic (this is not enough in most cases, but it is a good start).

We can try to build an isomorphism. How about we say

f (a) = b,

f (b) = c,

f (c) = d

and

f (d) = a .

This is definitely a bijection, but to make sure that the function is an isomorphism, we must make sure it respects the edge relation. In

G_{1},

vertices

a

and

b

are connected by an edge. In

G_{2},

f (a) = b

and

f (b) = c

are connected by an edge. So far, so good, but we must check the other three edges. The edge

{a, c}

G_{1}

corresponds to

{f (a), f (c)} = {b, d},

but here we have a problem. There is no edge between

b

and

d

G_{2} .

Thus

f

is NOT an isomorphism.

Not all hope is lost, however. Just because

f

is not an isomorphism does not mean that there is no isomorphism at all. We can try again. At this point it might be helpful to draw the graphs to see how they should match up.

$The graph G1 with four vertices arranged in a diamond. The top vertex (a) is connected to the three other vertices (d on the left, b on the right, and c below). There is one additional edge between d and c.$

$The graph G2 with four vertices arranged in a diamond. The top vertex (a) is connected to the vertices c below and b on the right. There is two additional edges between d (left) and c and between b and c .$

Alternatively, notice that in

G_{1},

the vertex

a

is adjacent to every other vertex. In

G_{2},

there is also a vertex with this property:

c .

So build the bijection

g : V_{1} \to V_{2}

by defining

g (a) = c

to start with. Next, where should we send

b ?

G_{1},

the vertex

b

is only adjacent to vertex

a .

There is exactly one vertex like this in

G_{2},

namely

d .

So let

g (b) = d .

As for the last two, in this example, we have a free choice: let

g (c) = b

and

g (d) = a

(switching these would be fine as well).

We should check that this really is an isomorphism. It is definitely a bijection. We must make sure that the edges are respected. The four edges in

G_{1}

are

{a, b}, {a, c}, {a, d}, {c, d} .

Under the proposed isomorphism these become

{g (a), g (b)}, {g (a), g (c)}, {g (a), g (d)}, {g (c), g (d)}

{c, d}, {c, b}, {c, a}, {b, a},

which are precisely the edges in

G_{2} .

Thus

g

is an isomorphism, so

G_{1} ≅ G_{2}

🔗

Sometimes we will talk about a graph with a special name (like

K_{n}

or the Petersen graph) or perhaps draw a graph without any labels. In this case, we are really referring to all graphs isomorphic to any copy of that particular graph. A collection of isomorphic graphs is often called an isomorphism class.

This is not unlike geometry, where we might have more than one copy of a particular triangle. There instead of isomorphic we say congruent.

🔗

There are other relationships between graphs that we care about, other than equality and being isomorphic. For example, compare the following pair of graphs:

🔗

$A graph with six vertices arranged in a hexagon, with edges between every possible pair of vertices.$

$Four vertices arranged in a diamond, with edges between every possible pair of vertices.$

These are definitely not isomorphic, but notice that the graph on the right looks like it might be part of the graph on the left, especially if we draw it like this:

🔗

$A graph with six vertices arranged in a hexagon with edges between every pair of vertices. Six edges are drawn in bold, forming a slanted rectangle with an X through it.$

We would like to say that the smaller graph is a subgraph of the larger.

🔗

We should give a careful definition of this. In fact, there are two reasonable notions for what a subgraph should mean.

🔗

Definition 2.1.6. Subgraphs.

We say that

G^{'} = (V^{'}, E^{'})

is a subgraph of

G = (V, E),

and write

G^{'} \subseteq G,

provided

V^{'} \subseteq V

and

E^{'} \subseteq E .

🔗

We say that

G^{'} = (V^{'}, E^{'})

is an induced subgraph of

G = (V, E)

provided

V^{'} \subseteq V

and every edge in

E

whose vertices are still in

V^{'}

is also an edge in

E^{'} .

🔗

Notice that every induced subgraph is also an ordinary subgraph, but not conversely. Think of a subgraph as the result of deleting some vertices and edges from the larger graph. For the subgraph to be an induced subgraph, we can still delete vertices, but now we only delete those edges that included the deleted vertices.

🔗

Example 2.1.7.

Consider the graphs:

🔗

$The graph G1 consisting of six vertices arranged in a triangle. Starting with the bottom left vertex and traveling around the triangle clockwise, the vertices are labeled a, d, f, e, c, b. Edges connect vertices at the corners of the triangle to vertices along their edges of the triangle. These center vertices are also connected to each of the other center vertices.$

$The graph G2 of four vertices: a horizontal row of three, labeled a, b, c, and a vertex labeled d centered between and above a and b. Edges connect a, b, and d (forming a triangle) and a fourth edge connects b to c.$

$The graph G3 of five vertices. Vertices a, b, and c are aligned in a horizontal row. Vertices d and f form a line with a in a line that slants up and to the right. There are edges between a and d, between d and f, between d and b, and between b and c.$

$The graph G4 with five vertices: a, b, and c form a horizontal row, d and f line up with a in a line slanting up and the to the right. The vertices form a triangle, and edges are arranged to fill in the outside border of the triangle. Vertices d and b are also connected by and edge.$

Here both

G_{2}

and

G_{3}

are subgraphs of

G_{1} .

But only

G_{2}

is an induced subgraph. Every edge in

G_{1}

that connects vertices in

G_{2}

is also an edge in

G_{2} .

G_{3},

the edge

{a, b}

is in

E_{1}

but not

E_{3},

even though vertices

a

and

b

are in

V_{3} .

🔗

The graph

G_{4}

is NOT a subgraph of

G_{1},

even though it looks like all we did is remove vertex

e .

The reason is that in

E_{4}

we have the edge

{c, f},

but this is not an element of

E_{1},

so we don’t have the required

E_{4} \subseteq E_{1} .

🔗

Back to some basic graph theory definitions. Notice that all the graphs we have drawn above have the property that no pair of vertices is connected more than once, and no vertex is connected to itself. Graphs like these are sometimes called simple, although we will just call them graphs. This is because our definition of a graph says that the edges form a set of 2-element subsets of the vertices. Remember that it doesn’t make sense to say a set contains an element more than once. So no pair of vertices can be connected by an edge more than once. Also, since each edge must be a set containing two vertices, we cannot have a single vertex connected to itself by an edge.

🔗

That said, there are times we want to consider double (or more) edges and single-edge loops. For example, the “graph” we drew for the Bridges of Königsberg problem had double edges because there really are two bridges connecting a particular island to the near shore. We will call these objects multigraphs. This is a good name: A multiset is a set in which we are allowed to include a single element multiple times.

🔗

The graphs above are also connected: you can get from any vertex to any other vertex by following some path of edges. A graph that is not connected can be thought of as two separate graphs drawn close together. For example, the following graph is NOT connected because there is no path from

a

b :

🔗

$A graph consisting of eight vertices arranged in two overlapping diamonds, with edges forming the border of those diamonds. The vertex on the far left is labeled a and the vertex on the far right is labeled b.$

Vertices in a graph do not always have edges between them. If we add all possible edges, then the resulting graph is called complete. That is, a graph is complete if every pair of vertices is connected by an edge. Since a graph is determined completely by which vertices are adjacent to which other vertices, there is only one complete graph with a given number of vertices. We give these a special name:

K_{n}

is the complete graph on

n

vertices.

🔗

Each vertex in

K_{n}

is adjacent to

n - 1

other vertices. We call the number of edges emanating from a given vertex the degree of that vertex. So every vertex in

K_{n}

has degree

n - 1 .

How many edges does

K_{n}

have? One might think the answer should be

n (n - 1),

since we count

n - 1

edges

n

times (once for each vertex). However, each edge is incident to 2 vertices, so we counted every edge exactly twice. Thus there are

n (n - 1) / 2

edges in

K_{n} .

Alternatively, we can say there are

(\binom{n}{2})

edges, since to draw an edge we must choose 2 of the

n

vertices.

🔗

In general, if we know the degrees of all the vertices in a graph, we can find the number of edges. The sum of the degrees of all vertices will always be twice the number of edges, since each edge adds to the degree of two vertices. Notice this means that the sum of the degrees of all vertices in any graph must be even!

🔗

This is our first example of a general result about all graphs. It seems innocent enough, but we will use it to prove all sorts of other statements. So let’s give it a name and state it formally.

🔗

Lemma 2.1.8. Handshake Lemma.

In any graph, the sum of the degrees of vertices in the graph is always twice the number of edges.

🔗

The handshake lemma

A lemma is a mathematical statement that is primarily of importance in that it is used to establish other results.

is sometimes called the degree sum formula, and can be written symbolically as

🔗

\sum_{v \in V} d (v) = 2 e .

Here we are using the notation

d (v)

for the degree of the vertex

v .

🔗

One use for the lemma is to actually find the number of edges in a graph. To do this, you must be given the degree sequence for the graph (or be able to find it from other information). This is a list of every degree of every vertex in the graph, generally written in non-increasing order.

🔗

Example 2.1.9.

How many vertices and edges must a graph have if its degree sequence is

🔗

(4, 4, 3, 3, 3, 2, 1) ?

🔗

Solution.

The number of vertices is easy to find. It is the number of degrees in the sequence: 7. To find the number of edges, we compute the degree sum

4 + 4 + 3 + 3 + 3 + 2 + 1 = 20,

so the number of edges is half this: 10.

🔗

The handshake lemma also tells us what is not possible.

🔗

Example 2.1.10.

At a recent math seminar, 9 mathematicians greeted each other by shaking hands. Is it possible that each mathematician shook hands with exactly 7 people at the seminar?

🔗

Solution.

It seems like this should be possible. Each mathematician chooses one person to not shake hands with. But this cannot happen. We are asking whether a graph with 9 vertices can have each vertex have degree 7. If such a graph existed, the sum of the degrees of the vertices would be

9 \cdot 7 = 63 .

This would be twice the number of edges (handshakes) resulting in a graph with

31.5

edges. That is impossible. Thus at least one (in fact an odd number) of the mathematicians must have shaken hands with an even number of people at the seminar.

🔗

We can generalize the previous example to get the following proposition.

A proposition is a general statement in mathematics, similar to a theorem, although generally of lesser importance.

🔗

Proposition 2.1.11.

In any graph, the number of vertices with odd degree must be even.

🔗

Proof.

Suppose there were a graph with an odd number of vertices with odd degree. Then the sum of the degrees in the graph would be odd, which is impossible, by the handshake lemma.

🔗

We will consider further applications of the handshake lemma in the exercises.

🔗

One final definition: We say a graph is bipartite if the vertices can be divided into two sets,

A

and

B,

with no two vertices in

A

adjacent and no two vertices in

B

adjacent. The vertices in

A

can be adjacent to some or all of the vertices in

B .

If each vertex in

A

is adjacent to all the vertices in

B,

then the graph is a complete bipartite graph, and gets a special name:

K_{m, n},

where

| A | = m

and

| B | = n .

🔗

Named Graphs.

Some graphs are used more than others and get special names.

🔗

$K_{n}$: The complete graph on $n$ vertices.
🔗
$K_{m, n}$: The complete bipartite graph with sets of $m$ and $n$ vertices.
🔗
$C_{n}$: The cycle on $n$ vertices, just one big loop.
🔗
$P_{n}$: The path on $n + 1$ vertices (so $n$ edges), just one long path.
🔗

🔗

$The graph K5: five vertices arranged in a pentagon. Each vertex is connected to each other vertex by an edge.$

$The graph K2,3: a row of two vertices on top and three on bottom. Each vertex in the top row is connected to each vertex on the bottom row.$

$The graph C6: a cycle of six vertices connected by six edges arranged as a hexagon.$

$The graph P5: six vertices connected by five edges. The first and last vertex have one edge, each other vertex has two edges (connecting to the previous and next vertex on the path).$

🔗

Graph Theory Definitions.

There are a lot of definitions to keep track of in graph theory. Here is a glossary of the terms we have already used and will soon encounter.

🔗

Graph: A collection of vertices, some of which are connected by edges. More precisely, a pair of sets $V$ and $E,$ where $V$ is a set of vertices and $E$ is a set of 2-element subsets of $V .$
🔗
Adjacent: Two vertices are adjacent if they are connected by an edge. Two edges are adjacent if they share a vertex.
🔗
Bipartite graph: A graph for which it is possible to divide the vertices into two disjoint sets such that there are no edges between any two vertices in the same set.
🔗
Complete bipartite graph: A bipartite graph for which every vertex in the first set is adjacent to every vertex in the second set.
🔗
Complete graph: A graph in which every pair of vertices is adjacent.
🔗
Connected: A graph is connected if there is a path from any vertex to any other vertex.
🔗
Chromatic number: The minimum number of colors required in a proper vertex coloring of the graph.
🔗
Cycle: A path (see below) that starts and stops at the same vertex, but contains no other repeated vertices.
🔗
Degree of a vertex: The number of edges incident to a vertex.
🔗
Euler trail: A walk which uses each edge exactly once.
🔗
Euler circuit: An Euler trail which starts and stops at the same vertex.
🔗
Multigraph: A multigraph is just like a graph but can contain multiple edges between two vertices as well as single edge loops (that is an edge from a vertex to itself).
🔗
Path: A path is a walk that doesn’t repeat any vertices (or edges) except perhaps the first and last. If a path starts and ends at the same vertex, it is called a cycle.
🔗
Planar: A graph which can be drawn (in the plane) without any edges crossing.
🔗
Subgraph: We say that $H$ is a subgraph of $G$ if every vertex and edge of $H$ is also a vertex or edge of $G .$ We say $H$ is an induced subgraph of $G$ if every vertex of $H$ is a vertex of $G$ and each pair of vertices in $H$ are adjacent in $H$ if and only if they are adjacent in $G$ .
🔗
Tree: A connected graph with no cycles. (If we remove the requirement that the graph is connected, the graph is called a forest.) The vertices in a tree with degree 1 are called leaves.
🔗
Vertex coloring: An assignment of colors to each of the vertices of a graph. A vertex coloring is proper if adjacent vertices are always colored differently.
🔗
Walk: A sequence of vertices such that consecutive vertices (in the sequence) are adjacent (in the graph). A walk in which no edge is repeated is called a trail, and a trail in which no vertex is repeated (except possibly the first and last) is called a path.
🔗

🔗

Reading Questions Reading Questions

1.

Is there more than one graph with five vertices and six edges? Explain what this question even means and how you would answer it.

🔗

2.

If a graph has 10 vertices, each with degree 4, how many edges does it have?

🔗

Number of edges:

🔗

3.

What questions do you have after reading this section? Write at least one question about the content of this section that you are curious about.

🔗

Exercises Practice Problems

1.

Consider the graph

Γ

🔗

Which of the graphs below is isomorphic to

Γ ?

🔗


A	B	C

Indicate the isomorphism by listing the vertices separated by commas in the order they correspond to A,B,C,D,E,F, respectively.

🔗

2.

Which of the following graphs are isomophic?

🔗


A	B


C	D

🔗

3.

The graph

G_{1}

has 7 vertices, all of degree 4. How many edges does

G_{1}

have? Answer:

🔗

The graph

G_{2}

has 8 vertices, all of degree

k .

Also,

G_{2}

has 20 edges. What is

k ?

Answer:

🔗

The graph

G_{3}

has

v

vertices, all of degree 4. Also,

G_{3}

has 16 edges. What is

v ?

Answer:

🔗

4.

I’m thinking of a graph which has degree sequence $(8,8,8,8,8,7,7,7,7)$. How many edges must my graph have?

🔗

5.

1. What is the largest

n

such that

P_{n}

is a subgraph of

K_{7} ?

🔗

2. What is the largest

n

such that

C_{n}

is a subgraph of

K_{7} ?

🔗

3. What is the largest

n

such that

P_{n}

is an induced subgraph of

K_{7} ?

🔗

4. What is the largest

n

such that

C_{n}

is an induced subgraph of

K_{7} ?

🔗

Hint.

Remember that

P_{n}

is the path that contains

n

edges and

n + 1

vertices.

🔗

Exercises Additional Exercises

1.

If 10 people each shake hands with each other, how many handshakes took place? What does this question have to do with graph theory?

🔗

2.

Among a group of 5 people, is it possible for everyone to be friends with exactly 2 of the people in the group? What about 3 of the people in the group?

🔗

3.

Is it possible for two different (non-isomorphic) graphs to have the same number of vertices and the same number of edges? What if the degrees of the vertices in the two graphs are the same (so both graphs have vertices with degrees 1, 2, 2, 3, and 4, for example)? Draw two such graphs or explain why not.

🔗

Hint.

Both situations are possible. Go find some examples.

🔗

4.

Are the two graphs below equal? Are they isomorphic? If they are isomorphic, give the isomorphism. If not, explain.

🔗

Graph 1:

V = {a, b, c, d, e},

E = {{a, b}, {a, c}, {a, e}, {b, d}, {b, e}, {c, d}}

🔗

Graph 2:

🔗

$A graph with five vertices arranged in a pentagon, labeled a through e, starting with the vertex at the top and proceeding counterclockwise. Edges between vertices a, c, and d make a triangle. Edges between b, c, d, and e form a quadralateral.$

🔗

5.

Consider the following two graphs:

🔗

$G_{1}$: $V_{1} = {a, b, c, d, e, f, g}$
🔗

$E_{1} = {{a, b}, {a, d}, {b, c}, {b, d}, {b, e},$
🔗

${b, f}, {c, g}, {d, e}, {e, f}, {f, g}} .$
🔗
$G_{2}$: $V_{2} = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}},$
🔗

$E_{2} = {{v_{1}, v_{4}}, {v_{1}, v_{5}}, {v_{1}, v_{7}}, {v_{2}, v_{3}}, {v_{2}, v_{6}},$
🔗

${v_{3}, v_{5}}, {v_{3}, v_{7}}, {v_{4}, v_{5}}, {v_{5}, v_{6}}, {v_{5}, v_{7}}} .$
🔗

Let $f : G_{1} \to G_{2}$ be a function that takes the vertices of Graph 1 to vertices of Graph 2. The function is given by the following table:

$x$ $a$ $b$ $c$ $d$ $e$ $f$ $g$

$f (x)$ $v_{4}$ $v_{5}$ $v_{1}$ $v_{6}$ $v_{2}$ $v_{3}$ $v_{7}$

Does $f$ define an isomorphism between Graph 1 and Graph 2?
Define a new function $g$ (with $g \neq f$ ) that defines an isomorphism between Graph 1 and Graph 2.
Is the graph pictured below isomorphic to Graph 1 and Graph 2? Explain.

$A graph with seven vertices. Six of the vertices are arranged in rectangle, three across and two down, with edges around the perimeter. The seventh vertex is in the center, with edges connecting it to the vertices directly above and below it, and to the two outside vertices in the bottom row.$

🔗

6.

What is the largest number of edges possible in a graph with 10 vertices? What is the largest number of edges possible in a bipartite graph with 10 vertices? What is the largest number of edges possible in a tree with 10 vertices?

🔗

Hint.

The bipartite graph is a little tricky. You will definitely want a complete bipartite graph, but it could be

K_{5, 5}

or maybe

K_{1, 9},

or …

🔗

7.

Which of the graphs below are bipartite? Justify your answers.

🔗

$A graph consisting of six vertices arranged in a hexagon. Edges connect each vertex to two others, but not in a cycle around the outside of the hexagon. However, following along the edges does visit every vertex.$

$A graph consisting of seven vertices arranged in a seven-sided polygon, with edges forming the perimeter of the polygon.$

$A graph consisting of a single vertex with eight edges connecting to eight vertices arranged in a circle around the central vertex.$

Hint.

The first graph is bipartite, which can be seen by labeling it as follows.

$A graph with five vertices. Four vertices make up the corners of a diamond; the last vertex is in the center. Edges form the perimeter of the diamond and connect the center vertex to the two corners on the left and right. The vertices on left and right are labeled A, the three vertices in the center column are each labeled B.$

Two of the remaining three are also bipartite.

🔗

8.

For which

n \geq 3

is the graph

C_{n}

bipartite?

🔗

Hint.

C_{4}

is bipartite;

C_{5}

is not. What about all the other values of

n ?

🔗

9.

For each of the following, try to give two different unlabeled graphs with the given properties, or explain why doing so is impossible.

🔗

Two different trees with the same number of vertices and the same number of edges. A tree is a connected graph with no cycles.
Two different graphs with 8 vertices all of degree 2.
Two different graphs with 5 vertices all of degree 4.
Two different graphs with 5 vertices all of degree 3.

🔗

10.

Decide whether the statements below about subgraphs are true or false. For those that are true, briefly explain why (1 or 2 sentences). For any that are false, give a counterexample.

🔗

Any subgraph of a complete graph is also complete.
Any induced subgraph of a complete graph is also complete.
Any subgraph of a bipartite graph is bipartite.
Any subgraph of a tree is a tree.

🔗

11.

We often define graph theory concepts using set theory. For example, given a graph

G = (V, E)

and a vertex

v \in V,

we define

🔗

N (v) = {u \in V : {v, u} \in E} .

We define

N [v] = N (v) \cup {v} .

The goal of this problem is to figure out what all this means.

🔗

Let $G$ be the graph with vertices $V$ and edges $E$ given by

$V = {a, b, c, d, e, f}, E = {{a, b}, {a, e}, {b, c}, {b, e}, {c, d}, {c, f}, {d, f}, {e, f}} .$

Find $N (a),$ $N [a],$ $N (c),$ and $N [c] .$
What are the largest and smallest possible values for $| N (v) |$ and $| N [v] |$ (the sizes of these sets) for the graph in part (a)? Explain.
Give an example of a graph $G = (V, E)$ (probably different from the one above) for which $N [v] = V$ for some vertex $v \in V .$ Is there a graph for which $N [v] = V$ for all $v \in V ?$ Explain.
Give an example of a graph $G = (V, E)$ for which $N (v) = \emptyset$ for some $v \in V .$ Is there an example of such a graph for which $N [u] = V$ for some other $u \in V$ as well? Explain.
Describe in words what $N (v)$ and $N [v]$ mean in general.

🔗

Hint.

You should be able to deduce everything directly from the definition. However, perhaps it would be helpful to know that the

N

stands for neighborhood.

🔗

12.

A graph is a way of representing the relationships between elements in a set: An edge between the vertices

x

and

y

tells us that

x

is related to

y

(which we can write as

x \sim y

). Not all sorts of relationships can be represented by a graph, though. For each relationship described below, either draw the graph or explain why the relationship cannot be represented by a graph.

🔗

The set $V = {1, 2, \dots, 9}$ and the relationship $x \sim y$ when $x - y$ is a non-zero multiple of 3.
The set $V = {1, 2, \dots, 9}$ and the relationship $x \sim y$ when $y$ is a multiple of $x .$
The set $V = {1, 2, \dots, 9}$ and the relationship $x \sim y$ when $0 < | x - y | < 3 .$

🔗

Hint.

Be careful to make sure the edges are not “directed.” In a graph, if

a

is adjacent to

b,

then

b

is adjacent to

a .

In the language of relations, we say that the edge relation is symmetric.

🔗

13.

Consider graphs with

n

vertices. Remember, graphs do not need to be connected.

🔗

How many edges must the graph have to guarantee at least one vertex has degree two or more? Prove your answer.
How many edges must the graph have to guarantee all vertices have degree two or more? Prove your answer.

🔗

Hint.

You might want to answer the questions for some specific values of

n

to get a feel for them, but your final answers should be in terms of

n .

🔗

14.

Prove that any graph with at least two vertices must have two vertices of the same degree.

🔗

Hint.

Try a small example first: Any graph with 8 vertices must have two vertices of the same degree. If not, what would the degree sequence be?

🔗

15.

Suppose

G

is a connected graph with

n > 1

vertices and

n - 1

edges. Prove that

G

has a vertex of degree 1.

🔗

Hint.

Use the handshake lemma 2.1.8. What would happen if all the vertices had degree 2?

🔗

16.

Which (if any) of the graphs below are the same?

🔗

$A graph with five vertices arranged in as a row of two on top and three on bottom. Edges connect each vertex in the top row to each vertex in the bottom row.$

$A graph with five vertices arranged in a pentagon. Each vertex is connected to its two neighbors around the pentagon by edges.$

$A graph with five vertices arranged in a diamond with one vertex in the middle. The top vertex is connected to the two outside vertices below it, which are connected to the bottom vertex. The center vertex is connected to the two vertices to its left and right.$

$A graph with five vertices arranged in a pentagon, with edges connecting each vertex to the two vertices farthest away from it (forming a 5-pointed star).$

$Five vertices arranged as a diamond with one vertex in the center. The center vertex has edges between it and each of the other vertices.$

The graphs above are unlabeled. Usually we think of a graph as having a specific set of vertices. Which (if any) of the graphs below are the same?

🔗

$A graph with six vertices arranged in two rows of three. The top vertices are labeled b, d, f from left to right. The bottom vertices are labeled a, c, e from left to right. Three edges connect each vertex in the top row to the vertex below it. Four more edges cross from a top vertex to a bottom vertex just to the left or right (forming two X’s).$

$A graph with six vertices arranged in two rows of three. The top vertices are labeled b, c, f from left to right. The bottom vertices are labeled a, d, e from left to right. Three edges connect each vertex in the top row to the vertex below it. Four more edges connect vertices along the top row and along the bottom row. Together this looks like two adjacent squares.$

$A graph with six vertices arranged in two rows of three. The top vertices are labeled c, b, f from left to right. The bottom vertices are labeled a, e, d from left to right. Three edges connect each vertex in the top row to the vertex below it. Four more edges cross from a top vertex to a bottom vertex just to the left or right (forming two X’s).$

$A graph with six vertices arranged in two rows of three. The top vertices are labeled v1, v2, v3 from left to right. The bottom vertices are labeled b6, v5, v4 from left to right. Three edges connect each vertex in the top row to the vertex below it. Four more edges connect vertices along the top row and along the bottom row. Together this looks like two adjacent squares.$

Actually, all the graphs above are just drawings of graphs. A graph is really an abstract mathematical object consisting of two sets

V

and

E,

where

E

is a set of 2-element subsets of

V .

Are the graphs below the same or different?

🔗

Graph 1:: $V = {a, b, c, d, e},$
🔗

$E = {{a, b}, {a, c}, {a, d}, {a, e}, {b, c}, {d, e}}$ .
🔗
Graph 2:: $V = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}},$
🔗

$E = {{v_{1}, v_{3}}, {v_{1}, v_{5}}, {v_{2}, v_{4}}, {v_{2}, v_{5}}, {v_{3}, v_{5}}, {v_{4}, v_{5}}} .$
🔗

🔗

You have attempted 1 of 14 activities on this page.

🔗

Prev Top Next

$x$	$a$	$b$	$c$	$d$	$e$	$f$	$g$
$f (x)$	$v_{4}$	$v_{5}$	$v_{1}$	$v_{6}$	$v_{2}$	$v_{3}$	$v_{7}$

Section 2.1 Problems and Definitions

Objectives

Subsection Section Preview

Investigate!

Worksheet Preview Activity A4US

1.

2.

3.

(a)

(b)

(c)

4.

5.

Subsection What is a Graph?

Definition 2.1.1. Graph.

Example 2.1.2.

Example 2.1.3.

Definition 2.1.4.

Example 2.1.5.

Definition 2.1.6. Subgraphs.

Example 2.1.7.

Lemma 2.1.8. Handshake Lemma.

Example 2.1.9.

Example 2.1.10.

Proposition 2.1.11.

Proof.

Named Graphs.

Graph Theory Definitions.

Reading Questions Reading Questions

1.

2.

3.

Exercises Practice Problems

1.

2.

3.

4.

5.

Exercises Additional Exercises

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Worksheet Preview Activity
A4 US