Vector Fields

Section 12.1 Vector Fields

Motivating Questions

What is a vector field?
What are some familiar contexts in which vector fields arise?
How do we draw a vector field?
How do gradients of functions with partial derivatives connect to vector fields?

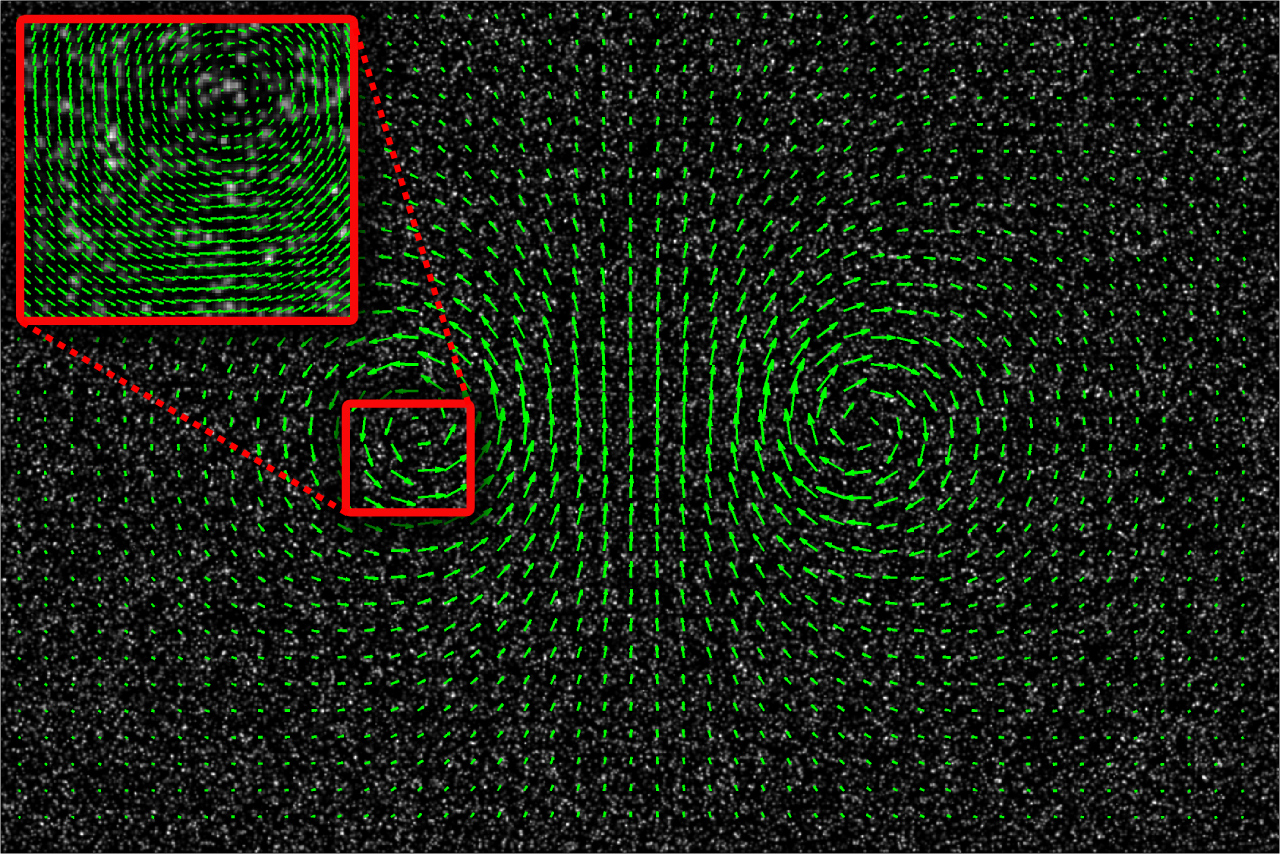
Vectors have played a central role in our study of multivariable calculus. We know how to do operations on vectors (addition, scalar multiplication, dot product, etc.), and we have seen how vectors can be used to describe curves in

R^{2}

and

R^{3} .

The examples of using vectors to describe curves was our first example of a vector-valued function. In Definition 9.6.2 a curve is traced by the terminal point of

r (t),

a function that has a real number as an input and produces a vector in

R^{2}

R^{3} .

In this section, we will expand our understanding of vector-valued functions to take a point

(x, y)

R^{2}

(or a point

(x, y, z)

R^{3}

) as an input and produce a vector (typically in

R^{2}

R^{3},

respectively) as output.

🔗

Preview Activity 12.1.1.

It’s common when discussing weather to talk about the wind speed, but as any student who has gotten this far in the text will know, this nomenclature is imprecise. It’s not terribly helpful to tell someone the wind is blowing at 10 ^km⁄_h without telling them the direction in which the wind is blowing. If you’re trying to make a decision based on what the wind is doing, you need to know about the direction as well. For instance, if you are taking off in a hot air balloon, the wind direction will determine which direction the chase team should start going to keep track of you. Because of the swirling nature of wind, it makes sense to give the wind velocity at each point in a region (two-dimensional or three-dimensional).

🔗

(a)

Suppose that given a point

(x, y)

in the plane, you know that the wind velocity at that point is given by the vector

⟨ y, x ⟩ .

For example, we’d then know that at the point

(1, - 1),

the wind velocity is

⟨ - 1, 1 ⟩ .

We will give the wind velocity as a function

F,

where

F (x, y) = ⟨ y, x ⟩ .

In the table below, fill in the wind velocity vectors for the given points.

🔗

$(x, y)$	$(2, 1)$	$(0, 0)$	$(- 1, 2)$	$(3, - 1)$	$(- 2, - 1)$
$F (x, y)$

🔗

(b)

Suppose that we associate the vector

G (x, y) = - x j

to a point

(x, y)

in the plane. Complete the table below by giving the vector associated to each of the given points.

🔗

$(x, y)$	$(- 2, 0)$	$(- 1, 2)$	$(0, - 2)$	$(2, 3)$	$(3, 2)$	$(- 1, 0)$	$(1, 3)$
$G (x, y)$

🔗

(c)

A table of values of these vector-valued functions is useful to understand the input vs. output nature of a vector field as a function, but perhaps even better is a method of visualizing the vector outputs. A good picture is worth a thousand words (or numbers). Returning to our analogy of the output vector for our vector field being wind velocity, if

F (2, 1) = ⟨ 1, 2 ⟩,

this means that at the location

(2, 1)

the wind is moving in the direction given by

⟨ 1, 2 ⟩ .

Thus, we draw the output vector

⟨ 1, 2 ⟩

with its initial point at

(2, 1) .

🔗

Using the first set of axes in Figure 12.1.1, plot the vectors

F (x, y)

for the five points in the table in part a. The example

F (1, - 1) = ⟨ - 1, 1 ⟩

is drawn for you.

🔗

(d)

Using the second set of axes in Figure 12.1.1, plot the vectors

G (x, y)

for the eight points in the table in part b.

🔗

described in detail following the image — Figure 12.1.1. Axes for plotting some vectors from $F (x, y)$ and $G (x, y) .$

🔗

Subsection 12.1.1 Examples of Vector Fields

As Preview Activity 12.1.1 showed, a velocity vector field is an example of a scenario where associating a vector to each point in a region is useful. We denote such a vector field by

F (x, y)

F (x, y, z),

where the vector associated to the point

(x, y)

(x, y, z)

is the velocity of something at that point. Wind velocity is one example, but another example would be the velocity of a flowing fluid. Figure 12.1.2 shows such a velocity vector field. Technically, it only shows some of the vectors in the vector field, since the figure would be unintelligible if all of the vectors were shown. This is illustrated by the inset in the upper left corner, which gives a better picture of what we would see if we zoomed in on the red square of the main figure.

🔗

Green vectors representing the velocity vectors of a flowing fluid. The vectors along the vertical axis of syymmetry are directed from bottom to top and are longest in the middle. Vectors on either side of the vertical axis of symmetry form circular rotation patterns, clockwise on the right and counterclockwise on the left. In the upper left corner, there is an inset figure that enlarges the center of rotation on the left side of the image. — Figure 12.1.2. An illustration of some of the vectors in a fluid velocity vector field. "PIVlab multipass" by Willa
¹
`commons.wikimedia.org/wiki/File:PIVlab_multipass.jpg#/media/File:PIVlab_multipass.jpg`
Licensed under CC-BY-SA 3.0 via Wikimedia Commons.
🔗

Force fields, such as those created by gravity, are also examples of vector fields. For example, the earth exerts a gravitational force on objects which is directed from the center of the object to the center of the earth. The magnitude of the force vector is determined by the distance between the object and the earth (by an reciprocal squared relationship.) An illustration of this vector field can be seen in Figure 12.1.3, where the earth is positioned at the origin, but not shown. Notice that the vectors get shorter as the distance from the origin increases, reflecting the fact that the gravitational force is weaker at larger distances from the origin (Earth).

🔗

Figure 12.1.3. Gravitational vector field.

🔗

Subsection 12.1.2 Mathematical Vector Fields

As suggested in the introduction and Preview Activity 12.1.1, vector fields can be specified using the notation of functions and vectors.

🔗

Definition 12.1.4.

A vector field in

2

-space is function whose value at a point

(x, y)

is a

2

-dimensional vector

F (x, y) .

Similarly, in

3

-space, a vector field is a function

F (x, y, z)

whose value at the point

(x, y, z)

is a

3

-dimensional vector.

🔗

Since

F (x, y, z)

is a vector, it has

i,

j,

and

k

components. Each of these components is a scalar function of the point

(x, y, z),

and so we will often write

🔗

F (x, y, z) = F_{1} (x, y, z) i + F_{2} (x, y, z) j + F_{3} (x, y, z) k

🔗

For example, if

F (x, y, z) = ⟨ x^{2}, x y \sin (z), y^{3} ⟩,

then the component functions of

F

would be

F_{1} (x, y, z) = x^{2},

F_{2} (x, y, z) = x y \sin (z),

and

F_{3} (x, y, z) = y^{3} .

Any time we are considering a vector field

F (x, y, z),

the definitions of functions

F_{1},

F_{2},

and

F_{3}

should be inferred in this manner. (For a vector field

F (x, y)

2

-space, we only have the functions

F_{1}

and

F_{2},

which are defined analogously.)

🔗

Subsection 12.1.3 Plotting Vector Fields

Preview Activity 12.1.1 gave you a chance to plot some vectors in the vector fields

F (x, y) = ⟨ y, x ⟩

and

G (x, y) = ⟨ 0, - x ⟩ .

It would be impossible to sketch all of the vectors in these vector fields, since there is one for every point in the plane. In fact, even sketching many more of the vectors than you were asked to in the preview activity rapidly becomes tedious. Fortunately, computers can do a great job of making such sketches. One thing to keep in mind, however, is that the magnitudes of the vectors in computer plots are typically scaled, including plots of vector fields we will encounter later in this text. To illustrate this, consider the two plots of the vector field

F (x, y) = y i + x j

in Figure 12.1.5.

🔗

The left plot shows some of the vectors and accurately depicts all of their magnitudes, making the figure very hard to understand, especially along the lines

y = x

and

y = - x .

The plot on the right, however, uses a uniform rescaling to make the figure easier to read. As before, each vector’s direction is completely accurate, but now the magnitudes are much smaller. However, the relative magnitudes are preserved, helping us to see that vectors farther from the origin have larger magnitude than those closer to the origin.

🔗

Activity 12.1.2.

The plot in Figure 12.1.6 illustrates the vector field

F (x, y) = y i - x j .

🔗

(a)

Starting with one of the vectors near the point

(2, 0),

sketch a curve that follows the direction of the vector field

F .

To help visualize what you are doing, it may be useful to think of the vector field as the velocity vector field for some flowing water and that you are imagining tracing the path that a tiny particle inserted into the water would follow as the water moves it around.

🔗

(b)

Repeat the previous step for at least two other starting points not on the curve you previously sketched.

🔗

(c)

What shape do the curves you sketched in the previous two steps form?

🔗

(d)

Verify that

F (x, y)

is orthogonal to

⟨ x, y ⟩ .

🔗

(e)

Calculate the gradient of the function

f (x, y) = x^{2} + y^{2}

and write a sentence comparing your result to the vector

x i + y j .

🔗

(f)

Write a sentence describing the geometric relationship between

F (x, y)

and a circle centered at the origin. What is the relationship between

| F (x, y) |

and the radius of that circle?

🔗

In the previous activity, we looked a special type of curve in a vector field, namely the curve that flows with the output of the vector field. Geometrically, the output vectors of the vector field will be tangent to the flow curves. These flow curves come up in several physical situations, including as solution curves to a system of differential equations. We will not discuss these applications here but you should should look out for uses of vector fields in the next few math courses.

🔗

Subsection 12.1.4 Gradient Vector Fields

Without using the terminology, we’ve actually already encountered one very important family of vector fields a number of times. Given a function

f

of two or three (or more!) variables, the gradient of

f

is a vector field, since for any point where

f

has first-order partial derivatives,

\nabla f

assigns a vector to that point (look at Subsection 10.6.3 for a review).

🔗

Activity 12.1.3.

(a)

In Figure 12.1.7 there are three sets of axes showing level curves for functions

f,

g,

and

h,

respectively. Sketch at least six vectors in the gradient vector field for each function. In making your sketches, you don’t have to worry about getting vector magnitudes precise, but you should ensure that the relative magnitudes (and directions) are correct for each function independently.

🔗

(b)

Verify that

F (x, y) = ⟨ 6 x y, 3 x^{2} + 9 \sqrt{y} ⟩

is a gradient vector field by finding a function

f

such that

\nabla f (x, y) = F (x, y) .

For reasons originating in physics, such a function

f

is called a potential function for the vector field

F .

🔗

(c)

Is the function

f

found in part b unique? That is, can you find another function

g

such that

\nabla g (x, y) = F (x, y)

but

f \neq g ?

🔗

(d)

Is the vector field

F (x, y) = 6 x y i + (2 x + 9 \sqrt{y}) j

a gradient vector field? Why or why not?

🔗

Subsection 12.1.5 Summary

A $2$ -dimensional vector field is a function defined on part of $R^{2}$ whose value is a $2$ -dimensional vector. A $3$ -dimensional vector field is a function defined on part of $R^{3}$ whose value is a $3$ -dimensional vector.
A vector field is typically described in terms of its multivariable component functions, $F (x, y) = ⟨ f (x, y), g (x, y) ⟩ = f (x, y) i + g (x, y) j$ or in 3D

$\begin{aligned} F (x, y, z) & = ⟨ f (x, y, z), g (x, y, z), h (x, y, z) ⟩ \\ = f (x, y, z) i + g (x, y, z) j + h (x, y, z) k . \end{aligned}$
Vector fields arise in familiar contexts such as wind velocity, fluid velocity, and gravitational force.
Vector fields are generally plotted in ways that ensure the direction and relative magnitudes of the vectors sketched are correct instead of ensuring that each vector’s magnitude is depicted correctly.
The gradient of a function $f$ of two or three variables is a vector field defined wherever $f$ has partial derivatives.

🔗

Exercises 12.1.6 Exercises

1.

Compute and sketch the vector assigned to the points

P = (0, 8, - 8)

and

Q = (2, 1, 0)

by the vector field

F = ⟨ x y, z^{2}, x ⟩ .

🔗

F (P) =

🔗

F (Q) =

🔗

2.

Suppose

\vec{F} = ⟨ - 2 y, 2 x ⟩ .

Complete the following table of values of

\vec{F} .

🔗

Values of

\vec{F}

🔗

$y = 1$
$y = 0$
$y = - 1$
	$x = - 1$	$x = 0$	$x = 1$

Using your table of values as a starting point, sketch this vector field on a piece of paper for

- 2 \leq x \leq 2

and

- 2 \leq y \leq 2 .

🔗

3.

Match the planar vector field

F = ⟨ 3 x + 3, y ⟩

with the corresponding plot in the Figures below.

🔗

\Leftarrow

Plot 1

🔗

\Leftarrow

Plot 2

🔗

\Leftarrow

Plot 3

🔗

\Leftarrow

Plot 4

🔗

With

a = 3

🔗

Answer :

🔗

Plot 2
Plot 3
Plot 4
Plot 1

🔗

4.

Assume that

x, y \geq 0

for all of the vector fields in this question. Select an answer for each question and explain your reasoning.

🔗

(a)

Let

F_{1} = y \vec{i} .

🔗

The vector field $F_{1}$ is
- parallel to the x-axis
- parallel to the y-axis
- neither
As $x$ increases, the length of the output vectors for $F_{1}$ will
- increase
- decrease
- neither
As $y$ increases, the length of the output vectors for $F_{1}$ will
- increase
- decrease
- neither

🔗

(b)

Let

F_{2} = ⟨ y, 1 ⟩ .

🔗

The vector field $F_{2}$ is
- parallel to the x-axis
- parallel to the y-axis
- neither
As $x$ increases, the length of the output vectors for $F_{2}$ will
- increase
- decrease
- neither
As $y$ increases, the length of the output vectors for $F_{2}$ will
- increase
- decrease
- neither

🔗

(c)

Let

F_{3} = (x + e^{1 - y}) \vec{j} .

🔗

The vector field $F_{3}$ is
- parallel to the x-axis
- parallel to the y-axis
- neither
As $x$ increases, the length of the output vectors for $F_{3}$ will
- increase
- decrease
- neither
As $y$ increases, the length of the output vectors for $F_{3}$ will
- increase
- decrease
- neither

🔗

(d)

Let

F_{4} = \nabla (y^{4} + e^{2 x}) .

🔗

The vector field $F_{4}$ is
- parallel to the x-axis
- parallel to the y-axis
- neither
As $x$ increases, the length of the output vectors for $F_{4}$ will
- increase
- decrease
- neither
As $y$ increases, the length of the output vectors for $F_{4}$ will
- increase
- decrease
- neither

🔗

Subsection 12.1.7 Notes to the Instructor

This section uses tools from the chapter on multivariable functions and thier derivatives, with specific references to gradients. Additionally, vector calculations and geometry are used throughout to understand the output of the vector field.

🔗

You have attempted 1 of 4 activities on this page.

🔗

Prev Top Next