4.9. Stack Diagrams for Recursive Functions

In the previous chapter we used a stack diagram to represent the state of a program during a function call. The same kind of diagram can make it easier to interpret a recursive function.

Remember that every time a function gets called it creates a new instance that contains the function’s local variables and parameters.

This figure shows a stack diagram for countdown, called with n = 3:

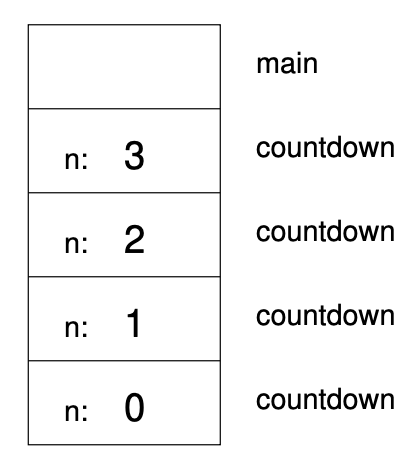
There is one instance of main and four instances of countdown, each with a different value for the parameter n. The bottom of the stack, countdown with n = 0 is the base case. It does not make a recursive call, so there are no more instances of countdown.

The instance of main is empty because main does not have any parameters or local variables. As an exercise, draw a stack diagram for nLines, invoked with the parameter n = 4.

Q-1: Refer to the nLines function below. It is the same as the nLines function defined on the previous page. How many instances of nLines would there be in the stack diagram if we begin with n = 4?

void nLines(int n) {
  if (n > 0) {
    cout << endl;
    nLines(n + 1);
  }
}

• 3
• If nLines could reach its base case, it cannot be done in 3 function calls.
• 4
• If nLines could reach its base case, it cannot be done in 4 function calls.
• 5
• If nLines could reach its base case, it could be done in 5 function calls, but does it ever reach the base case?
• infinite
• The nLines function never reaches its base case, so the stack diagram would be infinitely long.

You have attempted of activities on this page