5.9. El ordenamiento por inserción

El ordenamiento por inserción, aunque sigue siendo $O(n^2)$, funciona de una manera ligeramente diferente. Siempre mantiene una sublista ordenada en las posiciones inferiores de la lista. Cada ítem nuevo se “inserta” de vuelta en la sublista previa de manera que la sublista ordenada sea un ítem más larga. La Figura 4 muestra el proceso de ordenamiento por inserción. Los ítems sombreados representan las sublistas ordenadas a medida que el algoritmo lleva a cabo cada pasada.

Figura 4: ordenamientoPorInsercion

Figura 4: ordenamientoPorInsercion

Comenzamos asumiendo que una lista con un ítem (posición $0$) ya está ordenada. En cada pasada, una para cada ítem desde 1 hasta $n-1$, el ítem actual se comparara contra los de la sublista ya ordenada. A medida que revisamos en la sublista ya ordenada, desplazamos a la derecha los ítems que sean mayores. Cuando llegamos a un ítem menor o al final de la sublista, se puede insertar el ítem actual.

La Figura 5 muestra los detalles de la quinta pasada. En este punto del algoritmo, se tiene una sublista ordenada de cinco ítems que consta de los números 17, 26, 54, 77 y 93. Queremos insertar el 31 de vuelta en los ítems ya ordenados. La primera comparación con 93 hace que 93 se desplace hacia la derecha. El 77 y el 54 también se desplazan. Cuando se encuentra el ítem 26, el proceso de desplazamiento se detiene y el 31 se ubica en la posición disponible. Ahora tenemos una sublista ordenada de seis ítems.

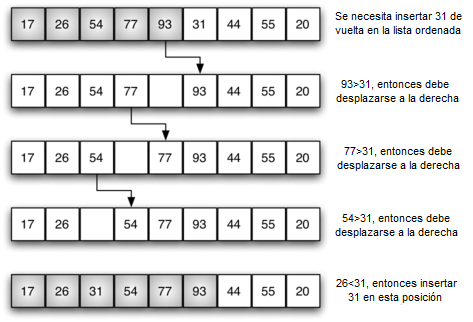
Figura 5: ordenamientoPorInsercion: Quinta pasada del ordenamiento

Figura 5: ordenamientoPorInsercion: Quinta pasada del ordenamiento

La implementación de ordenamientoPorInsercion (ActiveCode 1) muestra que se tienen de nuevo $n-1$ pasadas para ordenar los n ítems. La iteración comienza en la posición 1 y va hasta la posición $n-1$, ya que estos son los ítems que necesitan ser insertados de nuevo en las sublistas ordenadas. La línea 8 realiza la operación de intercambio que mueve un valor una posición hacia arriba en la lista, dejando espacio detrás de ella para la inserción. Recuerde que esto no es un intercambio completo como el que fue hecho en los algoritmos anteriores.

El número máximo de comparaciones para un ordenamiento por inserción es la suma de los primeros $n-1$ enteros. Nuevamente, esto es $O(n^2)$. Sin embargo, en el mejor de los casos, sólo se necesita hacer una comparación en cada pasada. Este sería el caso de una lista que ya estaba ordenada.

También es importante hacer una acotación sobre la diferencia entre desplazamiento e intercambio. En general, una operación de desplazamiento requiere aproximadamente un tercio de la carga de procesamiento de un intercambio ya que sólo se realiza una asignación. En las pruebas de referencia, el ordenamiento por inserción logrará un rendimiento muy bueno.

def ordenamientoPorInsercion(unaLista): for indice in range(1,len(unaLista)): valorActual = unaLista[indice] posicion = indice while posicion>0 and unaLista[posicion-1]>valorActual: unaLista[posicion]=unaLista[posicion-1] posicion = posicion-1 unaLista[posicion]=valorActual unaLista = [54,26,93,17,77,31,44,55,20] ordenamientoPorInsercion(unaLista) print(unaLista)

Initialize Run Stop
Beginning Step Forward Step Backward End

Autoevaluación

Q-3: Suponga que usted tiene que ordenar la siguiente lista de números: [15, 5, 4, 18, 12, 19, 14, 10, 8, 20] ¿Cuál de las siguientes listas representa la lista parcialmente ordenada tras tres pasadas completas del ordenamiento por inserción?

• [4, 5, 12, 15, 14, 10, 8, 18, 19, 20]
• Éste es un ordenamiento burbuja.
• [15, 5, 4, 10, 12, 8, 14, 18, 19, 20]
• Éste es el resultado de un ordenamiento por selección.
• [4, 5, 15, 18, 12, 19, 14, 10, 8, 20]
• El ordenamiento por selección opera al inicio de la lista. Cada pasada produce una lista ordenada más larga.
• [15, 5, 4, 18, 12, 19, 14, 8, 10, 20]
• El ordenamiento por inserción opera en el frente de la lista, no en el final.

You have attempted 1 of 3 activities on this page