4.10. Las torres de Hanoi¶
El rompecabezas de la Torre de Hanoi fue inventado por el matemático francés Edouard Lucas en 1883. Se inspiró en una leyenda acerca de un templo hindú donde el rompecabezas fue presentado a los jóvenes sacerdotes. Al principio de los tiempos, a los sacerdotes se les dieron tres postes y una pila de 64 discos de oro, cada disco un poco más pequeño que el de debajo. Su misión era transferir los 64 discos de uno de los tres postes a otro, con dos limitaciones importantes. Sólo podían mover un disco a la vez, y nunca podían colocar un disco más grande encima de uno más pequeño. Los sacerdotes trabajaban muy eficientemente, día y noche, moviendo un disco cada segundo. Cuando terminaran su trabajo, dice la leyenda, el templo se desmenuzaría en polvo y el mundo se desvanecería.
Aunque la leyenda es interesante, usted no tiene que preocuparse de que el final del mundo ocurra pronto en cualquier momento. El número de movimientos necesarios para mover correctamente una torre de 64 discos es \(2^{64}-1 = 18,446,744,073,709,551,615\). A una velocidad de un movimiento por segundo, ¡eso sería \(584,942,417,355\) años! Claramente hay algo más en este rompecabezas de lo que parece.
La Figura 1 muestra un ejemplo de una configuración de discos en el proceso de movimiento del primer poste al tercero. Observe que, según especifican las reglas, los discos de cada poste se apilan de manera que los discos más pequeños estén siempre encima de los discos más grandes. Si usted no ha intentado resolver este rompecabezas antes, debe probarlo ahora. No necesita discos y postes elegantes, una pila de libros o trozos de papel servirán.
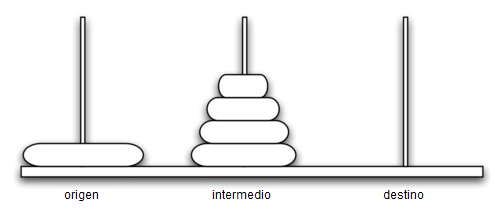
Figura 1: Una disposición ilustrativa de los discos para la Torre de Hanoi¶
Figura 1: Una disposición ilustrativa de los discos para la Torre de Hanoi
¿Cómo vamos a resolver este problema recursivamente? ¿Cómo resolvería usted este problema en todo caso? ¿Cuál es nuestro caso base? Pensemos en este problema desde abajo hacia arriba. Supongamos que usted tiene una torre de cinco discos, originalmente en un poste. Si usted ya sabía cómo mover una torre de cuatro discos al poste dos, entonces podría mover fácilmente el disco inferior al poste tres, y luego mover la torre de cuatro discos desde el poste dos al poste tres. Pero ¿qué tal si usted no sabe cómo mover una torre de altura cuatro? Supongamos que usted sabía cómo mover una torre de altura tres al poste tres; entonces sería fácil mover el cuarto disco al poste dos y mover los tres discos del poste tres encima de aquél. Pero ¿qué tal si usted no sabe cómo mover una torre de tres discos? ¿Qué tal si usted mueve una torre de dos discos al poste dos y luego mueve el tercer disco al poste tres, y luego mueve la torre de altura dos encima de dicho disco? Pero ¿qué tal si todavía no sabe cómo hacer esto? Seguramente estaría de acuerdo en que mover un solo disco al poste tres es bastante fácil, trivial incluso podría decirse. Esto suena como un caso base.
El siguiente es un esquema de alto nivel de cómo mover una torre desde el poste de origen, hasta el poste destino, utilizando un poste intermedio:
Mover una torre de altura-1 a un poste intermedio, utilizando el poste destino.
Mover el disco restante al poste destino.
Mover la torre de altura-1 desde el poste intermedio hasta el poste destino usando el poste de origen.
Siempre y cuando obedezcamos la regla de que los discos más grandes deben permanecer en la parte inferior de la pila, podemos usar los tres pasos anteriores recursivamente, tratando cualquier disco más grande como si ni siquiera estuviera allí. Lo único que falta en el esquema anterior es la identificación de un caso base. El problema de la torre de Hanoi más simple es una torre de un disco. En ese caso, sólo necesitamos mover un solo disco a su destino final. Una torre de un disco será nuestro caso base. Además, los pasos descritos anteriormente nos mueven hacia el caso base reduciendo la altura de la torre en los pasos 1 y 3. El Programa 1 muestra el código en Python para resolver el rompecabezas de la Torre de Hanoi.
Programa 1
1def moverTorre(altura,origen, destino, intermedio):
2 if altura >= 1:
3 moverTorre(altura-1,origen,intermedio,destino)
4 moverDisco(origen,destino)
5 moverTorre(altura-1,intermedio,destino,origen)
Note que el código en el Programa 1 es casi idéntico a la descripción en español. La clave de la simplicidad del algoritmo es que realizamos dos llamadas recursivas diferentes, una en la línea 3 y otra en la línea 5. En la línea 3 movemos todo menos el disco inferior de la torre de origen hacia un poste intermedio. La siguiente línea simplemente mueve el disco inferior a su lugar final. Luego, en la línea 5, movemos la torre desde el poste intermedio hasta la parte superior del disco más grande. El caso base se detecta cuando la altura de la torre es 0; en ese caso no habrá nada que hacer, por lo que la función moverTorre simplemente regresa el control. Lo importante a tener en cuenta al tratar el caso base de esta manera es que simplemente el regreso desde moverTorre es lo que finalmente permite que la función moverDisco sea invocada.
La función moverDisco, que se muestra en el Programa 2, es muy simple. Todo lo que hace es imprimir que se está moviendo un disco de un poste a otro. Si usted codifica y ejecuta el programa moverTorre podrá ver que le da una solución muy eficiente al rompecabezas.
Programa 2
def moverDisco(desde,hacia):
print("mover disco de",desde,"a",hacia)
El programa en el ActiveCode 1 proporciona la solución completa para tres discos.
Ahora que usted ha visto el código para moverTorre y moverDisco, es posible que se pregunte por qué no tenemos una estructura de datos que realice explícitamente un seguimiento de qué discos están en qué postes. He aquí una sugerencia: si usted fuera a supervisar explícitamente los discos, utilizaría probablemente tres objetos Pila, uno para cada poste. La respuesta es que Python proporciona implícitamente las pilas que necesitamos a través de la pila de llamadas.