7.2. Vocabulario y definiciones¶
Ahora que hemos visto algunos ejemplos de grafos, definiremos más formalmente un grafo y sus componentes. Ya conocemos algunos de estos términos desde nuestra discusión sobre los árboles.
- Vértice
Un vértice (también llamado “nodo”) es una parte fundamental de un grafo. Puede tener un nombre, que llamaremos “clave”. Un vértice también puede tener información adicional. A esta información adicional la llamaremos “carga útil”.
- Arista
Una arista (también llamada “arco”) es otra parte fundamental de un grafo. Una arista conecta dos vértices para mostrar que hay una relación entre ellos. Las aristas pueden ser unidireccionales o bidireccionales. Si las aristas de un grafo son todas unidireccionales, decimos que el grafo es un grafo dirigido o un digrafo. El grafo de prerrequisitos de asignaturas que se muestra arriba es claramente un digrafo ya que se deben tomar algunas asignaturas antes que otras.
- Ponderación
Las aristas pueden ponderarse para mostrar que hay un costo para ir de un vértice a otro. Por ejemplo, en un grafo de carreteras que conectan una ciudad con otra, la ponderación en la arista puede representar la distancia entre las dos ciudades.
Con esas definiciones a mano podemos definir formalmente un grafo. Un grafo puede ser representado por \(G\) donde \(G=(V,E)\). Para el grafo \(G\), \(V\) es un conjunto de vértices y \(E\) es un conjunto de aristas. Cada arista es una tupla \((v,w)\) donde \(w,v \in V\). Podemos añadir un tercer componente a la tupla de la arista para representar una ponderación. Un subgrafo \(s\) es un conjunto de aristas \(e\) y de vértices \(v\) tales que \(e \subset E\) y \(v \subset V\).
La Figura 2 muestra otro ejemplo de un digrafo ponderado simple. Formalmente podemos representar este grafo como el conjunto de seis vértices:
y el conjunto de nueve aristas:
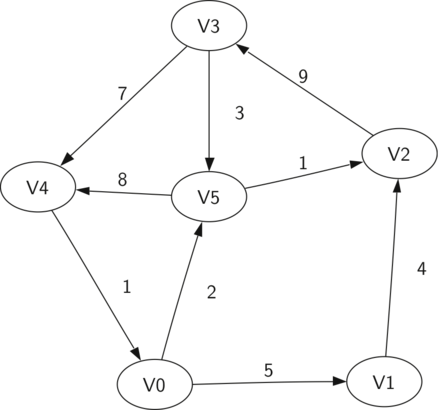
Figura 2: Un ejemplo simple de un grafo dirigido¶
Figura 2: Un ejemplo simple de un grafo dirigido
El grafo de ejemplo en la Figura 2 ayuda a ilustrar otros dos términos clave de los grafos:
- Ruta
Una ruta en un grafo es una secuencia de vértices que están conectados por las aristas. Formalmente definiríamos una ruta como \(w_1, w_2, ..., w_n\) tal que \((w_i, w_{i+1}) \in E\) para todo \(1 \le i \le n-1\). La longitud de la ruta no ponderada es el número de aristas en la ruta, específicamente \(n-1\). La longitud ponderada de la ruta es la suma de las ponderaciones de todos las aristas en la trayectoria. Por ejemplo, en la Figura 2 la ruta desde \(V3\) hasta \(V1\) es la secuencia de vértices \((V3,V4,V0,V1)\). Las aristas son \(\left\{(v3,v4,7),(v4,v0,1),(v0,v1,5) \right\}\).
- Ciclo
Un ciclo en un grafo dirigido es una ruta que comienza y termina en el mismo vértice. Por ejemplo, en la Figura 2 la ruta \((V5,V2,V3,V5)\) es un ciclo. Un grafo sin ciclos se denomina grafo acíclico. Un grafo dirigido sin ciclos se denomina grafo acíclico dirigido o GAD. Veremos que podemos resolver varios problemas importantes si el problema se puede representar como un GAD.