2.7. Diccionarios

La segunda estructura de datos principal de Python es el diccionario. Como usted probablemente recordará, los diccionarios difieren de las listas en que usted puede acceder a los ítems de un diccionario mediante una clave en lugar de una posición. Más adelante en este libro verá que hay muchas maneras de implementar un diccionario. Lo que es más importante notar ahora mismo es que las operaciones para obtener y asignar ítems en un diccionario son \(O(1)\). Otra operación importante de los diccionarios es la operación de pertenencia. Comprobar si una clave está o no en el diccionario es también \(O(1)\). La eficiencia de todas las operaciones con diccionarios se resume en la Tabla 3. Una acotación importante sobre el desempeño de los diccionarios es que las eficiencias que se presentan en la tabla son para un desempeño promedio. En algunos casos raros, las operaciones de pertenencia, obtención y asignación de ítems pueden degenerar en desempeños \(O(n)\), pero vamos a adentrarnos en eso en un capítulo posterior cuando hablemos de las diferentes maneras en que podría implementarse un diccionario.

Tabla 3: Eficiencia O-grande de las operaciones de diccionarios en Python

operación	Eficiencia O-grande
copiar	O(n)
obtener ítem	O(1)
asignar ítem	O(1)
eliminar ítem	O(1)
pertenencia (in)	O(1)
iteración	O(n)

Para nuestro último experimento de desempeños, compararemos el desempeño de la operación de pertenencia entre listas y diccionarios. En el proceso confirmaremos que el operador de pertenencia para las listas es \(O(n)\) y que el operador de pertenencia para los diccionarios es \(O(1)\). El experimento que vamos a utilizar para comparar los dos casos es simple. Haremos una lista con un rango de números en ella. Luego seleccionaremos números al azar y veremos si los números están o no en la lista. Si nuestras tablas de desempeño son correctas, entre más grande sea la lista, mayor debería ser el tiempo que toma determinar si cierto número está contenido en ella.

Repetiremos el mismo experimento para un diccionario que contiene números como claves. En este experimento deberíamos notar que la determinación de si un número está en el diccionario no sólo es mucho más rápida, sino que el tiempo que se tarda la comprobación debería permanecer constante a medida que el diccionario se hace más grande.

El Programa 6 implementa esta comparación. Observe que estamos realizando exactamente la misma operación, número in contenedor. La diferencia es que en la línea 7 x es una lista, y en la línea 9 x es un diccionario.

Programa 6

import timeit
import random

for i in range(10000,1000001,20000):
    t = timeit.Timer("random.randrange(%d) in x"%i,
                     "from __main__ import random,x")
    x = list(range(i))
    tiempo_lista = t.timeit(number=1000)
    x = {j:None for j in range(i)}
    tiempo_diccionario = t.timeit(number=1000)
    print("%d,%10.3f,%10.3f" % (i, tiempo_lista, tiempo_diccionario))

La Figura 4 resume los resultados de la ejecución del Programa 6. Usted puede ver que el diccionario es consistentemente más rápido. Para el tamaño de lista más pequeño (de 10,000 elementos), un diccionario es 89.4 veces más rápido que una lista. ¡Para el tamaño de la lista más grande (de 990,000 elementos) el diccionario es 11,603 veces más rápido! Usted también puede ver que el tiempo que tarda el operador de pertencia en el caso de la lista crece linealmente con el tamaño de la misma. Esto verifica la afirmación de que el operador de pertencia en una lista es \(O(n)\). También puede verse que el tiempo para el operador de pertenencia en un diccionario es constante, incluso a medida que crece el tamaño del diccionario. De hecho, para un diccionario de tamaño 10,000 la operación de pertenencia tomó 0.004 milisegundos y para el diccionario de tamaño 990,000 también tomó 0.004 milisegundos.

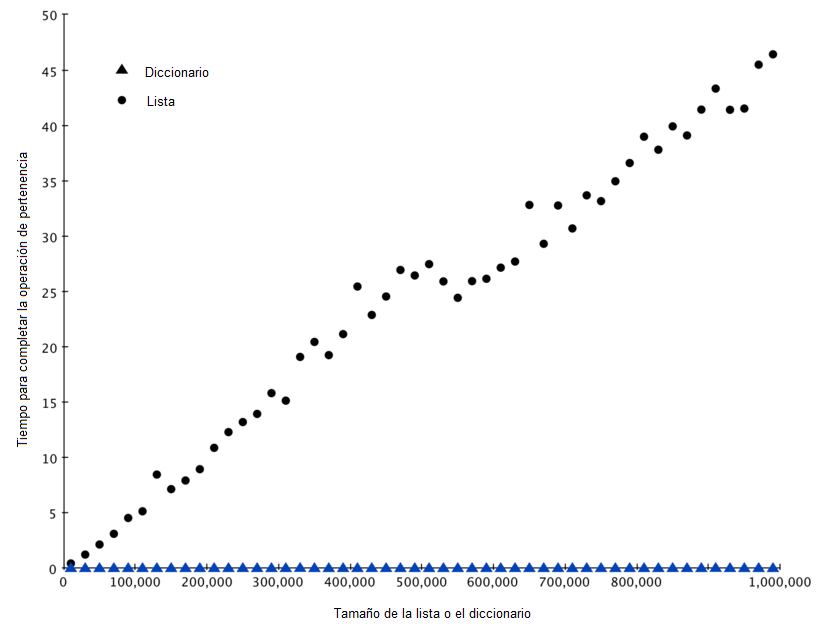
Figura 4: Comparación del operador in para listas y diccionarios en Python

Figura 4: Comparación del operador in para listas y diccionarios en Python

Dado que Python es un lenguaje en evolución, siempre hay cambios que suceden entre bastidores. La información más reciente sobre el rendimiento de las estructuras de datos de Python se puede encontrar en el sitio web de Python. Desde que se escribió este texto, la wiki de Python tiene una agradable página de complejidades de tiempo que se puede consultar en la página titulada Time Complexity Wiki.

Autoevaluación

Q-1: ¿Cuál de las operaciones sobre listas que se muestran a continuación no es O(1)?

• lista.pop(0)
• Cuando usted quita el primer elemento de una lista, todos los demás elementos de la lista deben desplazarse hacia adelante.
• lista.pop()
• Eliminar un elemento del final de la lista es una operación constante.
• lista.append()
• Añadir al final de la lista es una operación constante
• lista[10]
• Indizar una lista es una operación constante
• todas las anteriores son O(1)
• Hay una operación que requiere que todos los demás elementos de lista se muevan.

Q-2: ¿Cuál de las operaciones sobre diccionarios que se muestran a continuación es O(1)?

• 'x' in miDiccionario
• ``in`` es una operación constante para un diccionario porque no tiene que iterar pero hay una respuesta mejor.
• del miDiccionario['x']
• Borrar un elemento de un diccionario es una operación constante, pero hay una respuesta mejor.
• miDiccionario['x'] == 10
• La asignación a una clave de diccionario es constante pero hay una respuesta mejor.
• miDiccionario['x'] = miDiccionario['x'] + 1
• La reasignación a una clave de diccionario es constante pero hay una respuesta mejor.
• todas las anteriores son O(1)
• Las únicas operaciones de diccionario que no son O(1) son aquéllas que requieren iteración.

You have attempted of activities on this page