6.15. Search Tree Analysis¶
With the implementation of a binary search tree now complete, we will do
a quick analysis of the methods we have implemented. Let’s first look at
the put method. The limiting factor on its performance is the height
of the binary tree. Recall from the vocabulary section that the height
of a tree is the number of edges between the root and the deepest leaf
node. The height is the limiting factor because when we are searching
for the appropriate place to insert a node into the tree, we will need
to do at most one comparison at each level of the tree.
What is the height of a binary tree likely to be? The answer to this question depends on how the keys are added to the tree. If the keys are added in a random order, the height of the tree is going to be around \(\log_2{n}\) where \(n\) is the number of nodes in the tree. This is because if the keys are randomly distributed, about half of them will be less than the root and about half will be greater than the root. Remember that in a binary tree there is one node at the root, two nodes in the next level, and four at the next. The number of nodes at any particular level is \(2^d\) where \(d\) is the depth of the level. The total number of nodes in a perfectly balanced binary tree is \(2^{h+1}-1\), where \(h\) represents the height of the tree.
A perfectly balanced tree has the same number of nodes in the left
subtree as the right subtree. In a balanced binary tree, the worst-case
performance of put is \(O(\log_2{n})\), where \(n\) is
the number of nodes in the tree. Notice that this is the inverse
relationship to the calculation in the previous paragraph. So
\(\log_2{n}\) gives us the height of the tree and represents the
maximum number of comparisons that put will need to do as it
searches for the proper place to insert a new node.
Unfortunately it is possible to construct a search tree that has height
\(n\) simply by inserting the keys in sorted order! An example of
this is shown in Figure 6. In this case the
performance of the put method is \(O(n)\).
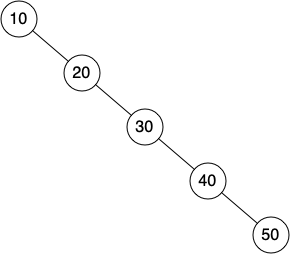
Figure 6: A skewed binary search tree would give poor performance¶
Now that you understand that the performance of
the put method is limited by the height of the tree, you can
probably guess that other methods, get, in, and del, are limited
as well. Since get searches the tree to find the key, in the worst
case the tree is searched all the way to the bottom and no key is found.
At first glance del might seem more complicated since it may need
to search for the successor before the deletion operation can complete.
But remember that the worst-case scenario to find the successor is also
just the height of the tree which means that you would simply double the
work. Since doubling is a constant factor, it does not change worst-case analysis
of \(O(n)\) for an unbalanced tree.