4.23. Implementing an Ordered List¶

In order to implement the ordered list, we must remember that the relative positions of the items are based on some underlying characteristic. The ordered list of integers given above (17, 26, 31, 54, 77, and 93) can be represented by a linked structure as shown in Figure 15. Again, the node and link structure is ideal for representing the relative positioning of the items.

../_images/orderlinkedlist.png — Figure 15: An Ordered Linked List¶

To implement the OrderedList class, we will use the same technique as seen previously with unordered lists. Once again, an empty list will be denoted by a head reference to None (see Listing 8).

Listing 8

class OrderedList:
    def __init__(self):
        self.head = None

As we consider the operations for the ordered list, we should note that the isEmpty and size methods can be implemented the same as with unordered lists since they deal only with the number of nodes in the list without regard to the actual item values. Likewise, the remove method will work just fine since we still need to find the item and then link around the node to remove it. The two remaining methods, search and add, will require some modification.

The search of an unordered linked list required that we traverse the nodes one at a time until we either find the item we are looking for or run out of nodes (None). It turns out that the same approach would actually work with the ordered list and in fact in the case where we find the item it is exactly what we need. However, in the case where the item is not in the list, we can take advantage of the ordering to stop the search as soon as possible.

For example, Figure 16 shows the ordered linked list as a search is looking for the value 45. As we traverse, starting at the head of the list, we first compare against 17. Since 17 is not the item we are looking for, we move to the next node, in this case 26. Again, this is not what we want, so we move on to 31 and then on to 54. Now, at this point, something is different. Since 54 is not the item we are looking for, our former strategy would be to move forward. However, due to the fact that this is an ordered list, that will not be necessary. Once the value in the node becomes greater than the item we are searching for, the search can stop and return False. There is no way the item could exist further out in the linked list.

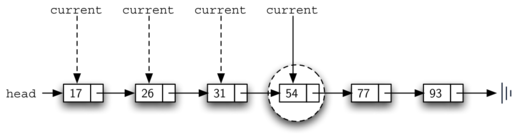
../_images/orderedsearch.png — Figure 16: Searching an Ordered Linked List¶

Listing 9 shows the complete search method. It is easy to incorporate the new condition discussed above by adding another boolean variable, stop, and initializing it to False (line 4). While stop is False (not stop) we can continue to look forward in the list (line 5). If any node is ever discovered that contains data greater than the item we are looking for, we will set stop to True (lines 9–10). The remaining lines are identical to the unordered list search.

Listing 9

def search(self,item):
    current = self.head
    found = False
    stop = False
    while current != None and not found and not stop:
        if current.getData() == item:
            found = True
        else:
            if current.getData() > item:
                stop = True
            else:
                current = current.getNext()

    return found

The most significant method modification will take place in add. Recall that for unordered lists, the add method could simply place a new node at the head of the list. It was the easiest point of access. Unfortunately, this will no longer work with ordered lists. It is now necessary that we discover the specific place where a new item belongs in the existing ordered list.

Assume we have the ordered list consisting of 17, 26, 54, 77, and 93 and we want to add the value 31. The add method must decide that the new item belongs between 26 and 54. Figure 17 shows the setup that we need. As we explained earlier, we need to traverse the linked list looking for the place where the new node will be added. We know we have found that place when either we run out of nodes (current becomes None) or the value of the current node becomes greater than the item we wish to add. In our example, seeing the value 54 causes us to stop.

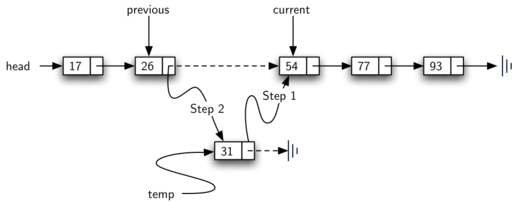
../_images/linkedlistinsert.png — Figure 17: Adding an Item to an Ordered Linked List¶

As we saw with unordered lists, it is necessary to have an additional reference, again called previous, since current will not provide access to the node that must be modified. Listing 10 shows the complete add method. Lines 2–3 set up the two external references and lines 9–10 again allow previous to follow one node behind current every time through the iteration. The condition (line 5) allows the iteration to continue as long as there are more nodes and the value in the current node is not larger than the item. In either case, when the iteration fails, we have found the location for the new node.

The remainder of the method completes the two-step process shown in Figure 17. Once a new node has been created for the item, the only remaining question is whether the new node will be added at the beginning of the linked list or some place in the middle. Again, previous == None (line 13) can be used to provide the answer.

Listing 10

def add(self,item):
    current = self.head
    previous = None
    stop = False
    while current != None and not stop:
        if current.getData() > item:
            stop = True
        else:
            previous = current
            current = current.getNext()

    temp = Node(item)
    if previous == None:
        temp.setNext(self.head)
        self.head = temp
    else:
        temp.setNext(current)
        previous.setNext(temp)

The OrderedList class with methods discussed thus far can be found in ActiveCode 1. We leave the remaining methods as exercises. You should carefully consider whether the unordered implementations will work given that the list is now ordered.

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None

def getData(self):
        return self.data

def getNext(self):
        return self.next

def setData(self,newdata):
        self.data = newdata

def setNext(self,newnext):
        self.next = newnext

class OrderedList:
    def __init__(self):
        self.head = None

def search(self,item):
        current = self.head
        found = False
        stop = False
        while current != None and not found and not stop:
            if current.getData() == item:
                found = True
            else:
                if current.getData() > item:
                    stop = True
                else:
                    current = current.getNext()

return found

def add(self,item):
        current = self.head
        previous = None
        stop = False
        while current != None and not stop:
            if current.getData() > item:
                stop = True
            else:
                previous = current
                current = current.getNext()

temp = Node(item)
        if previous == None:
            temp.setNext(self.head)
            self.head = temp
        else:
            temp.setNext(current)
            previous.setNext(temp)

def isEmpty(self):
        return self.head == None

def size(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()

return count

mylist = OrderedList()
mylist.add(31)
mylist.add(77)
mylist.add(17)
mylist.add(93)
mylist.add(26)
mylist.add(54)

print(mylist.size())
print(mylist.search(93))
print(mylist.search(100))

4.23.1. Analysis of Linked Lists¶

To analyze the complexity of the linked list operations, we need to consider whether they require traversal. Consider a linked list that has n nodes. The isEmpty method is \(O(1)\) since it requires one step to check the head reference for None. size, on the other hand, will always require n steps since there is no way to know how many nodes are in the linked list without traversing from head to end. Therefore, length is \(O(n)\). Adding an item to an unordered list will always be O(1) since we simply place the new node at the head of the linked list. However, search and remove, as well as add for an ordered list, all require the traversal process. Although on average they may need to traverse only half of the nodes, these methods are all \(O(n)\) since in the worst case each will process every node in the list.

You may also have noticed that the performance of this implementation differs from the actual performance given earlier for Python lists. This suggests that linked lists are not the way Python lists are implemented. The actual implementation of a Python list is based on the notion of an array. We discuss this in more detail in Chapter 8.

You have attempted of activities on this page