In your own words, explain how sea surface temperature, moisture, and wind interact to create strong hurricanes - or weaken them.
Section 1.3 Investigation C: Modelling Hurricanes
A model is an artificial representation or a simplification of something more complicated, like a toy airplane. Models can be useful in making predictions (e.g., weather models) or to help us better understand the phenomena under study. For example, what factors impact the severity of a hurricane?
-
Move the red hurricane symbol to a circle on the map and read what happens.
-
Switch between the Sea Surface Temperature, Moisture, and Wind maps to see the data for each circle.
-
Which circles create the strongest hurricanes? Why?
Checkpoint 1.3.1. Explain Hurricane Formation.
Checkpoint 1.3.2. Evaluate Model Accuracy.
Explain how you could evaluate the accuracy of this model of hurricane strength. What would you do next if you decided the model was not appropriate?
In this course, you will encounter two main types of models: statistical models and probability/simulation models. For example, the Random Babies simulation in Investigation B, allowed you to simulate hypothetical data to estimate probabilities of different events. As long as the model valid, we can predict that all four mothers receiving the correct babies would not happen very often in the long run. Most models rely on simplifying assumptions, like babies being returned “completely at random.”
The graphs below show histograms of the hurricane data with different probability models (red curves).
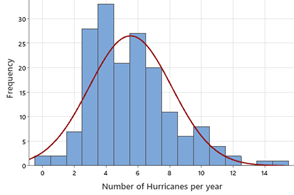
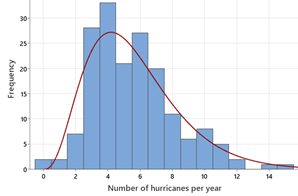
Checkpoint 1.3.4. Compare Graphical Displays.
Describe the difference between a histogram and a dotplot. When might histograms be more useful?
Checkpoint 1.3.5. Select Best Model.
Which model (red curve) do you consider a better match to the observed data?
Checkpoint 1.3.6. Define Statistical Model.
What does the term “model” mean in this situation? Why would such a model be useful? What assumptions would you need to make? [Hint: Which do you consider more likely, a year with 13 hurricanes or with 14?]
To get an idea of a statistical model, you will collect some data:
-
Using a measurement tool provided by your instructor, measure the circumference of a tennis ball.
Checkpoint 1.3.7. Record Your Measurement.
Record your measurement here (to the nearest hundredths place): cm
Checkpoint 1.3.8. Examine Measurement Variation.
Did everyone in class find the same value? What are some possible explanations for different measurements?
We can think of these measurements as observations from a random process, which we can summarize with a statistical model. If we consider 28.5cm the “true value,” then we can write our statistical model as
Measurement recorded = 28.5 + random error
Checkpoint 1.3.9. Estimate Measurement Error.
How could we estimate the likely amount of random error in your class’s measurement process?
Much of what scientists do is try to measure, explain, and minimize the amount of random variation.
Checkpoint 1.3.10. Reduce Measurement Error.
Suggest a way to reduce the measurement error in your class’s process.
Checkpoint 1.3.11. Understand Measurement Model.
What does the term “model” mean here? Why would such a model be useful? What assumptions need to be made?
Subsection 1.3.1 Practice Problem C.A
Researchers often compare data generated from a model to observed data to help validate the model. If the model’s data reasonably matches the observed data, that helps confirm that they (the model builders) understand the underlying data generating process.
Open this app to model the tennis ball measurement random process: https://iambethchance.shinyapps.io/Modeling8/
Checkpoint 1.3.12. Model Sources of Variation.
Suggest and label four possible sources of variation in the tennis ball measurements. Enter them as the four pie charts and conjecture sizes and probabilities for those sources (e.g., right now, Spinner 1 assumes a perfect measurement with 0.50 probability, a -.1 cm error with 0.25 probability and a +.1 cm error with 0.25 probability). Include a screen capture of your random process.
Checkpoint 1.3.13. Simulate One Measurement.
Simulate one measurement by pressing the Simulate data button. What did you find for the total random error across your four sources? Will this be the same every time?
Checkpoint 1.3.14. Compare Simulated to Observed Data.
Generate the same number of measurements as we took in class. Compare the simulated data to the actual data from class (e.g., shape, center, spread). What looks similar and what looks different?
Checkpoint 1.3.15. Adjust the Model.
Suggest a way to adjust the model that you think will lead to simulated data that better matches the observed data. Briefly justify your choice.
Subsection 1.3.2 Practice Problem C.B
Suppose human body temperatures can be modelled with a normal distribution with mean 98.6°F. Suppose you take repeated measures of your temperature over several days.
Checkpoint 1.3.16. Identify Believable Distribution.
Which distribution below do you think is more believable? Briefly justify your choice.
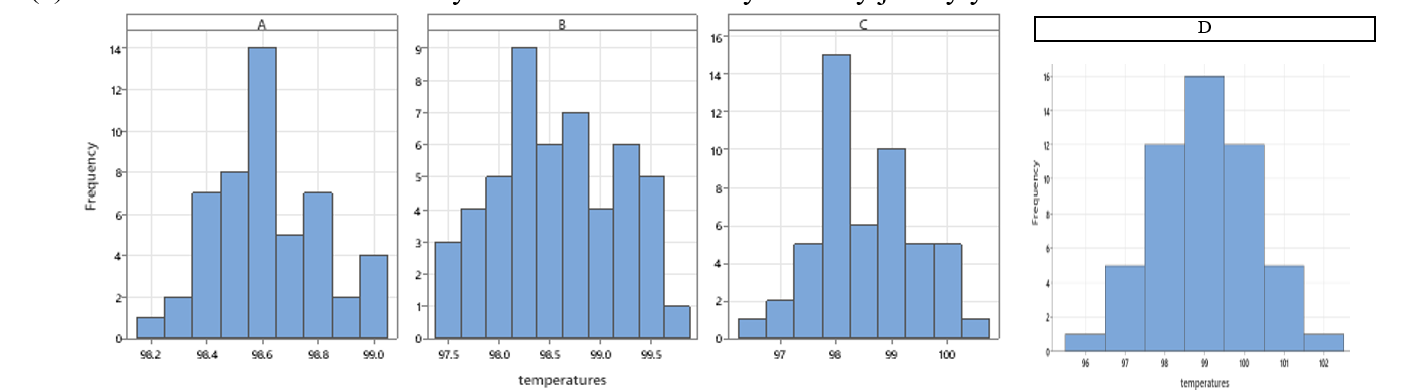
Checkpoint 1.3.17. Evaluate Suspicious Distribution.
Explain why you might be suspicious if someone told you Distribution D was their results.
Checkpoint 1.3.18. Sources of Variation.
Suggest four possible sources of variation in your body temperature measurements.
Checkpoint 1.3.19. Compare Standard Deviations.
Distributions A-C have the same mean (98.6) but different spread or variability. Which of the graphs above has the largest standard deviation? Approximate the value of each standard deviation by interpreting the standard deviation as a “typical” deviation from the mean.
Checkpoint 1.3.20. Evaluate Distribution Assumptions.
The 4 distributions are all “bell-shaped and symmetric.” Do you think actual repeated body measurements on the same individual will behave this way? Briefly explain your reasoning.
Checkpoint 1.3.21.
Suppose I randomly select one of the temperatures from Distribution C. Approximate the probability that the temperature is larger than 99°F. Interpret your probability in context.
You have attempted of activities on this page.
