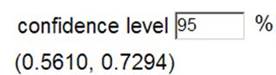Skip to main content

ISCAM: Investigating Statistical Concepts, Applications, and Methods

Beth L. Chance, Allan J. Rossman

Section 3.3 Investigation 1.9: Kissing the Right Way (cont.)

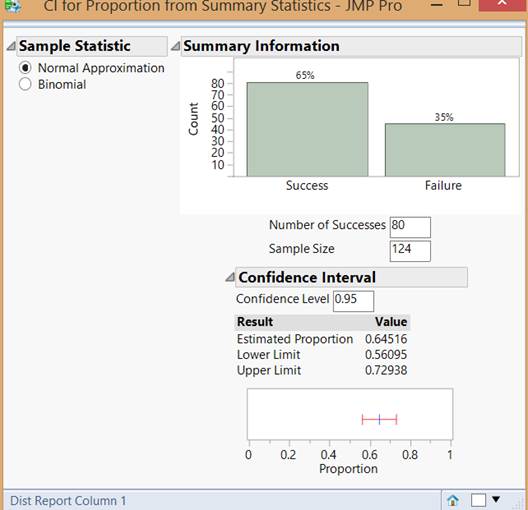
Recall the study published in Nature that found 64.5% of 124 kissing couples leaned right to kiss (Investigation 1.6). We previously used simulation and the binomial distribution to determine which values were plausible for the underlying probability that a kissing couple leans right (\(\pi\)). In particular, we found 0.5 and 0.74 were not plausible values for \(\pi\) but 0.6667 was. The 95% Clopper-Pearson Binomial confidence interval was (0.554, 0.729). Now you will consider applying the normal model as another method for producing confidence intervals for this parameter.
🔗

Checkpoint 3.3.1. Check CLT Validity Condition.

With a sample size of 124 kissing couples, does the Central Limit Theorem predict the normal probability distribution will be a reasonable model for the distribution of the sample proportion?
🔗
Hint.
Check whether you have at least 10 successes and at least 10 failures in your sample.
🔗
🔗
Solution.
\(n\pi \geq 10\) and \(n(1-\pi) \geq 10\text{.}\) Since we don’t have an estimate for \(\pi\text{,}\) use \(\hat{p}\text{:}\)
🔗
\(n\hat{p} = 124(0.645) = 80 > 10\)
🔗
\(n(1-\hat{p}) = 124(0.355) = 44 > 10\)
🔗
Yes! Both conditions are satisfied, so the CLT validity condition is met.
🔗
🔗
🔗
When you do not have a particular value to be tested for the process probability, it’s reasonable to use the sample proportion in checking the sample size condition for the CLT. (This is equivalent to making sure there are at least 10 successes and at least 10 failures in the sample.)
🔗

Checkpoint 3.3.2. Describe Distribution of Sample Proportion.

Do you have enough information to describe and sketch the distribution of the sample proportion as predicted by the Central Limit Theorem? Explain.
🔗
Hint.
According to the CLT, what are the mean and standard deviation of the distribution of sample proportions?
🔗
🔗
Solution.
No, you do not have enough information to sketch the distribution predicted by the CLT. We need \(\text{SD}(\hat{p}) = \sqrt{\pi(1-\pi)/n}\text{,}\) but we don’t know \(\pi\text{.}\)
🔗
🔗
🔗

Checkpoint 3.3.3. Estimate Standard Deviation.

Suggest one method for estimating the standard deviation of this distribution of sample proportions based on the observed sample data. Calculate this estimate.
🔗
Method:
🔗
Estimate:
🔗
Hint.
What value could you substitute for \(\pi\) in the formula \(\sqrt{\pi(1-\pi)/n}\text{?}\)
🔗
🔗
Solution.
Method: Use \(\text{SE}(\hat{p}) = \sqrt{\hat{p}(1-\hat{p})/n}\)
🔗
Estimate: \(\text{SE}(\hat{p}) = \sqrt{0.645(0.355)/124} = \sqrt{0.001846} = 0.043\)
🔗
🔗
🔗

Definition.

The standard error of the sample proportion, \(\text{SE}(\hat{p})\text{,}\) is an estimate for the standard deviation of \(\hat{p}\) (i.e., \(\text{SD}(\hat{p})\)) based on the sample data, found by substituting the sample proportion for \(\pi\text{:}\)
\begin{equation*} \text{SE}(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \end{equation*}
🔗
🔗

Checkpoint 3.3.4. Find Largest Plausible Distance.

Now consider calculating a 95% confidence interval for the process probability \(\pi\) based on the observed sample proportion \(\hat{p}\text{.}\) What’s the largest distance you expect to see a sample proportion \(\hat{p}\) fall away from the underlying process probability \(\pi\text{?}\) [Hint: Assuming a normal distribution … 95% …]
🔗
Largest plausible distance =
🔗
Hint.
For a normal distribution, approximately 95% of observations fall within how many standard deviations of the mean?
🔗
🔗
Solution.
Max plausible distance = \(2 \times 0.043 = 0.086\) (95% of the time)
🔗
🔗
🔗

Checkpoint 3.3.5. Calculate Confidence Interval.

Use the distance in (d) and the observed sample proportion of \(\hat{p} = 0.645\) to determine an interval of plausible values for \(\pi\text{,}\) the probability that a kissing couple leans to the right.
🔗
Interval:
🔗
Hint.
Add and subtract the distance from part (d) to the sample proportion.
🔗
🔗
Solution.
\(\pi\) should fall within 2 standard deviations of the observed sample proportion. So \(\pi\) is at least \(0.645 - 2(0.043) = 0.559\) and at most \(0.645 + 2(0.043) = 0.731\)
🔗
I’m 95% confident that the probability a kissing couple leans right is between 0.559 and 0.731.
🔗
🔗
🔗
An approximate 95% confidence interval for the process probability based on the normal distribution would be \(\hat{p} \pm 2\sqrt{\hat{p}(1-\hat{p})/n}\text{.}\) That is, this interval extends two standard deviations on each side of the sample proportion. We know that for the normal distribution roughly 95% of observations (here sample proportions) fall within 2 SDs of the mean (here the unknown process probability), so this method will "capture" the process probability for roughly 95% of samples.
🔗
However, we should admit that the multiplier of 2 is a bit of a simplification. So how do we find a more precise value of the multiplier to use, including for values other than 95%?
🔗

Definition.

The \((100 \times C)\)% critical value, \(z^*\text{,}\) is the \(z\)-score value such that \(P(-z^* \leq Z \leq z^*) = C\) where \(C\) is any specified probability value, and \(Z\) represents a normal distribution with mean 0 and SD 1.
🔗
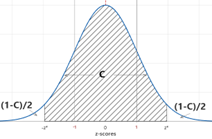
Critical value illustration showing shaded middle area under normal curve
Note: We use the symbol \(z^*\) to distinguish this value, found based on the confidence level, from \(z_0\text{,}\) the observed \(z\)-score for the data.
🔗
🔗

Technology Detour — Finding Percentiles from the Standard Normal Distribution.

Use technology to more precisely determine the number of standard deviations that capture the middle 95% of the normal distribution with mean = 0 and standard deviation = 1. [Hint: In other words, how many standard deviations do you need to go on each side of zero to capture the middle 95% of the standard normal distribution?] Keep in mind that the \(z\)-value corresponding to probability \(C\) in the middle of the distribution, also corresponds to having probability \((1-C)/2\) in each tail.
🔗

Checkpoint 3.3.6. Finding Critical Values with Normal Probability Calculator.

In Normal Probability Calculator applet:
🔗
  • You can leave the mean set to zero and the standard deviation to 1 and the variable is "z-scores."
    🔗
    🔗
  • Check the box next to the first \(<\) sign and specify the probability value to correspond to the lower tail probability of interest: \((1-C)/2\text{.}\) Press Enter/Return and it will display the negative \(z^*\)-value.
    🔗
    🔗
🔗
🔗

Checkpoint 3.3.7. Finding Critical Values in R.

In R: The iscaminvnorm function takes the following inputs:
🔗
  • Probability of interest (prob1)
    🔗
    🔗
  • mean = the mean of the normal distribution (default = 0)
    🔗
    🔗
  • sd = the standard deviation of the normal distribution (default = 1)
    🔗
    🔗
  • direction = whether the probability of interest was in the lower tail ("below") or the upper tail ("above"), in both tails ("outside"), or in the middle of the distribution ("between")
    🔗
    🔗
🔗
For example: iscaminvnorm(prob1 = 0.95, direction = "between")
🔗
🔗

Checkpoint 3.3.8. Finding Critical Values in JMP.

In JMP using the Distribution Calculator in the ISCAM Journal File:
🔗
  1. From the Distribution pull-down menu, select Normal (at the top of the list)
    🔗
    🔗
  2. Specify the values for the mean (0) and standard deviation (1)
    🔗
    🔗
  3. Change the Type of Calculation to Input probability and calculate quantiles
    🔗
    🔗
  4. Select Central Probability and specify the confidence level (e.g., 0.95)
    🔗
    🔗
  5. Press Enter/Return.
    🔗
    🔗
🔗
🔗
🔗

Checkpoint 3.3.9. Compare 90% Critical Value.

Find the critical value for a 90% confidence interval. Is it larger or smaller than with 95% confidence? Why does this make sense?
🔗
  • Smaller
  • The same
  • Larger
Hint.
Use technology to find the critical value for 90% confidence. Think about what happens to the interval width when you require less confidence.
🔗
🔗
Solution.
\(z^*(90) = 1.645 < 1.96\)
🔗
This makes sense because we are only capturing the middle 90% so don’t have to extend as far from the middle.
🔗
🔗
🔗

One Sample \(z\)-Confidence Interval (Wald Interval) for \(\pi\).

When we have at least 10 successes and at least 10 failures in the sample, an approximate confidence interval for \(\pi\) is given by:
\begin{equation*} \hat{p} \pm z^* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \end{equation*}
where \(z^*\) corresponds to the confidence level.
🔗
🔗

Checkpoint 3.3.10. Identify Midpoint and Width.

Based on this formula, what (expression) is midpoint of the confidence interval? What (expression) is the width of the interval?
🔗
Hint.
The interval is \(\hat{p} \pm z^* \sqrt{\hat{p}(1-\hat{p})/n}\text{.}\) What’s the center? What’s the distance from the lower bound to the upper bound?
🔗
🔗
Solution.
Midpoint: \(\hat{p}\)
🔗
Width: \(2 \times z^* \sqrt{\hat{p}(1-\hat{p})/n}\)
🔗
🔗
🔗

Checkpoint 3.3.11. Effect of Confidence Level on Width.

How does increasing the confidence level affect the width of the interval?
🔗
  • The width does not change
  • Increases the width
  • Decreases the width
Hint.
What happens to \(z^*\) when the confidence level increases?
🔗
🔗
Solution.
Increasing the Confidence Level \(\Rightarrow\) increase \(z^*\) \(\Rightarrow\) wider interval
🔗
🔗
🔗

Checkpoint 3.3.12. Effect of Sample Size on Width.

How does increasing the sample size affect the width of the interval?
🔗
  • The width does not change
  • Increases the width
  • Decreases the width
Hint.
Look at the formula for the margin of error. What happens to \(\sqrt{\hat{p}(1-\hat{p})/n}\) as \(n\) increases?
🔗
🔗
Solution.
Increasing \(n\) \(\Rightarrow\) smaller width (\(n\) is in the denominator)
🔗
🔗
🔗

Definition.

The half-width of a confidence interval is also referred to as the margin of error.
🔗
So the above interval formula is of the common form: statistic \(\pm\) margin of error, where margin of error = critical value \(\times\) standard error of statistic. Here, margin of error = \(z^* \sqrt{\hat{p}(1-\hat{p})/n}\text{.}\)
🔗
🔗
Although 95% is the most common confidence level, a few other confidence levels and their corresponding critical values are shown in the table below.
🔗
Table 3.3.13. Common Critical Values
🔗
Confidence level 90% 95% 99% 99.9%
Critical value \(z^*\) 1.645 1.960 2.576 3.291

Checkpoint 3.3.14. Calculate and Compare 90% Interval.

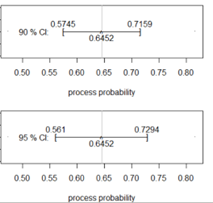
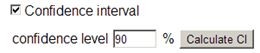
Use technology (see Technology Detour below) to find and report the 90% \(z\)-confidence interval for the probability that a kissing couple leans to the right. How do the midpoint and width of the 90% confidence interval compare to those of the 95% confidence interval?
🔗
90% interval:
🔗
Comparison:
🔗
Hint.
Use the critical value from the table (1.645) or technology to find the 90% interval.
🔗
🔗
Solution.
If the confidence level is 90%, then use \(z^* = 1.645\)
🔗
\(0.645 - 1.645 \times 0.043 = 0.5743\)
🔗
\(0.645 + 1.645 \times 0.043 = 0.7157\)
🔗
I am 90% confident that between 57.43% and 71.57% of kissing couples turn to the right.
🔗
Midpoint = \((0.5743 + 0.7157)/2 = 0.645\) (same as with the 95% confidence interval)
🔗
Width = \(0.7157 - 0.5743 = 0.142\) (smaller than for the 95% confidence interval)
🔗
\(2(1.645)(0.043) = 0.142\)
🔗
Comparison of 90% and 95% confidence intervals showing different widths with same midpoint
🔗
🔗

Technology Detour — One Proportion \(z\)-Confidence Intervals.

Checkpoint 3.3.15. \(z\)-interval with R.

Use iscamonepropztest(observed, n, hypothesized, alternative="greater", "less," or "two.sided", conf.level)
🔗
You can enter either the number of successes or the proportion of successes (\(\hat{p}\)) for the "observed" value. If you don’t specify a hypothesized value and alternative, be sure to label the confidence level.
🔗
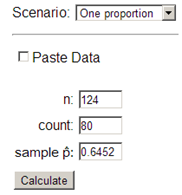
For example: iscamonepropztest(observed=80, n=124, conf.level=0.95)
🔗
Solution.
Running the command in R will produce output including the 95% confidence interval:
🔗
R output showing 95% z-confidence interval for kissing study
🔗
🔗

Checkpoint 3.3.16. \(z\)-interval with JMP.

  1. Open the ISCAM Journal file and select Confidence Interval for One Proportion
    🔗
    🔗
  2. Specify Raw Data (column of outcomes) or Summary Stats
    🔗
    🔗
  3. With Summary Stats, keep the radio button set to Normal Approximation
    🔗
    🔗
🔗
Solution.
JMP will display output including the 95% confidence interval:
🔗
JMP output showing 95% z-confidence interval for kissing study
🔗
🔗

Checkpoint 3.3.17. \(z\)-interval with Theory-Based Inference applet.

Using the Theory-Based Inference applet:
🔗
  1. Keep the pull-down menu set to One proportion.
    🔗
    🔗
  2. Specify the sample size \(n\) and either the count or the sample proportion. Or check the Paste Data box and paste in the individual outcomes (check the Includes header box if you are also copying over the variable name).
    🔗
    🔗
  3. Press Calculate.
    🔗
    🔗
  4. Check the box for Confidence interval
    🔗
    🔗
  5. Change the confidence level from 95 to 90%
    🔗
    🔗
  6. Press the Calculate CI button
    🔗
    🔗
🔗
Theory-Based Inference applet interface showing input fieldsTheory-Based Inference applet showing confidence interval options
Solution.
The applet will display output including the confidence interval:
🔗
Theory-Based Inference applet output showing z-confidence interval for kissing study
🔗
🔗
🔗

Checkpoint 3.3.18. Compare to Exact Binomial Intervals.

How do the widths of the \(z\)-intervals compare to the Exact Binomial Confidence Intervals reported by R?
🔗
  • 90 percent confidence interval: 0.5684, 0.7166
    🔗
    🔗
  • 95 percent confidence interval: 0.5542, 0.7290
    🔗
    🔗
🔗
Hint.
Calculate the widths of both the \(z\)-intervals and the exact binomial intervals for comparison.
🔗
🔗
Solution.
The binomial confidence intervals are a bit longer (and even a bit more to the left).
🔗
🔗
🔗

Sample Size Determination.

Checkpoint 3.3.19. Determine Required Sample Size.

Suppose you are planning your own study about kissing couples. Before you collect the data, you know you would like the margin of error to be at most 3 percentage points and that you will use a 95% confidence level. Use this information to determine the sample size necessary for your study.
🔗
[This is a very common question asked of statisticians. Think about how to determine this using the \(z\)-interval formula. What information do you know? What information are you looking for?]
🔗
Approach 1: Use the sample proportion found in the original study as an estimate for the unknown value of \(\pi\text{.}\)
🔗
\(n =\)
🔗
Approach 2: Without a preliminary study, you can use 0.5 as an estimate of this probability.
🔗
\(n =\)
🔗
Hint.
Set the margin of error equal to 0.03 and solve for \(n\text{:}\) \(z^* \sqrt{\pi(1-\pi)/n} = 0.03\)
🔗
🔗
Solution.
\(z^* \sqrt{\hat{p}(1-\hat{p})/n} = 0.03\)
🔗
Approach 1: Use the previous \(\hat{p} = 0.645\text{.}\)
🔗
Solving for \(n\text{,}\) we would get \((1.96^2)(0.645)(0.355)/(0.03^2) = 977.4\) or 978
🔗
Approach 2: Using 0.50
🔗
Solving for \(n\text{,}\) we would get \((1.96^2)(0.5)(0.5)/(0.03^2) = 1067.1\) or 1068.
🔗
🔗
🔗

Checkpoint 3.3.20. Compare Sample Size Approaches.

How does the sample size required differ based on how you estimate \(\pi\) in the calculation? Why is Approach 2 considered a "conservative" approach?
🔗
Hint.
Compare the sample sizes from the two approaches. When is \(\pi(1-\pi)\) largest?
🔗
🔗
Solution.
The value of \(n\) increases for probabilities closer to 0.50. If the process probability is not 0.50, the recommended \(n\) value will result in a smaller margin of error than requested.
🔗
🔗
🔗
We can solve for \(n\) by inverting the formula for the margin of error, assuming a value for \(\pi\text{.}\) The largest value for the margin of error occurs when \(\pi = 0.50\text{,}\) so that value can be used for a conservative estimate of the necessary sample size. You should always round your value up to the next integer to also ensure the margin of error won’t exceed the specification. Notice that this calculation is much more difficult with a binomial confidence interval which does not have a simple formula to manipulate.
🔗
🔗

Subsection 3.3.1 Practice Problem 1.9A

Recall from Practice Problem 1.8B that a student wanted to assess whether her dog Muffin tends to chase her blue ball and her red ball equally often when they are rolled at the same time. The student rolled both balls a total of 96 times, each time keeping track of which ball Muffin chased. The student found that Muffin chased the blue ball 52 times and the red ball 44 times. We arbitrarily decided to treat the blue ball as "success."
🔗

Checkpoint 3.3.21. Check Validity of \(z\)-procedures.

Is using theory-based \(z\)-procedures valid in this study? How are you deciding?
🔗
Solution.
Yes, \(z\)-procedures are valid. We have 52 successes and 44 failures, both at least 10, so the validity condition is satisfied.
🔗
🔗
🔗

Checkpoint 3.3.22. Calculate 95% Confidence Interval.

Determine and interpret a 95% \(z\)-confidence interval.
🔗
Solution.
\(\hat{p} = 52/96 = 0.542\text{,}\) \(\text{SE}(\hat{p}) = \sqrt{0.542(0.458)/96} = 0.051\)
🔗
95% CI: \(0.542 \pm 1.96(0.051) = 0.542 \pm 0.100 = (0.442, 0.642)\)
🔗
We are 95% confident that the probability Muffin chases the blue ball is between 0.442 and 0.642.
🔗
🔗
🔗

Checkpoint 3.3.23. Compare Margins of Error.

Report the margin of error of your interval. Determine and compare to the margin of error change if with a 99% confidence level.
🔗
Solution.
Margin of error for 95%: 0.100
🔗
For 99% (\(z^* = 2.576\)): \(2.576(0.051) = 0.131\)
🔗
The margin of error increases when we require more confidence (99% vs 95%).
🔗
🔗
🔗

Checkpoint 3.3.24. Determine Required Sample Size.

What would be the necessary sample size if we wanted a margin of error of 0.01 for a confidence level of 95%? Explain how you are finding this.
🔗
Solution.
Using \(\pi = 0.542\text{:}\)
🔗
\(n = \frac{0.542(0.458)}{(0.01/1.96)^2} \approx 9552\)
🔗
We would need approximately 9,552 trials to achieve a margin of error of 0.01 (1 percentage point) with 95% confidence.
🔗
🔗
🔗
🔗

Subsection 3.3.2 Practice Problem 1.9B

Checkpoint 3.3.25. Understanding Confidence Intervals.

In an actual study, how do you know whether your interval actually contains the value of the unknown parameter?
🔗
Solution.
In an actual study, you never know for certain whether your specific interval contains the unknown parameter. The parameter is a fixed value, and your interval either contains it or doesn’t. The confidence level refers to the long-run proportion of intervals that would contain the parameter if we repeated the study many times.
🔗
🔗
🔗

Checkpoint 3.3.26. Standard Deviation vs Standard Error.

What is the distinction between standard deviation and standard error?
🔗
Solution.
Standard deviation refers to the actual variability in the distribution (e.g., \(\text{SD}(\hat{p}) = \sqrt{\pi(1-\pi)/n}\)), which depends on the unknown parameter \(\pi\text{.}\) Standard error is an estimate of the standard deviation calculated from the sample data (e.g., \(\text{SE}(\hat{p}) = \sqrt{\hat{p}(1-\hat{p})/n}\)), where we substitute the sample proportion for the unknown parameter.
🔗
🔗
🔗
Reconsider Muffin from Subsection 3.2.2 and suppose our confidence interval is (0.2689, 0.4811). For each statement below, determine whether it is a valid or invalid interpretation of this confidence interval.
🔗

Checkpoint 3.3.27.

Statement 1: You are 95% confident that the interval (0.2689, 0.4811) contains the sample proportion of blue balls chased by Muffin.
🔗
  • Valid
  • Incorrect. We know the sample proportion exactly; there’s no need for a confidence interval for it. The confidence interval is for the parameter (the true probability), not the sample proportion.
  • Invalid
  • Correct! We know the sample proportion exactly; there’s no need for a confidence interval for it. The confidence interval is for the parameter (the true probability), not the sample proportion.
🔗

Checkpoint 3.3.28.

Statement 2: There is a 95% chance that the interval (0.2689, 0.4811) captures the probability Muffin chasing the blue ball.
🔗
  • Valid
  • Incorrect. This makes it sound like the parameter is random, when it’s actually fixed. The interval is what’s random. Once we’ve constructed this specific interval, it either contains the parameter or it doesn’t.
  • Invalid
  • Correct! This makes it sound like the parameter is random, when it’s actually fixed. The interval is what’s random. Once we’ve constructed this specific interval, it either contains the parameter or it doesn’t.
🔗

Checkpoint 3.3.29.

Statement 3: 95% of the time the interval (0.2689, 0.4811) contains the probability of Muffin chasing the blue ball.
🔗
  • Valid
  • Incorrect. This specific interval is fixed; it doesn’t change. The correct interpretation is about the procedure (95% of intervals constructed this way contain the parameter), not this specific interval.
  • Invalid
  • Correct! This specific interval is fixed; it doesn’t change. The correct interpretation is about the procedure (95% of intervals constructed this way contain the parameter), not this specific interval.
🔗

Checkpoint 3.3.30.

Statement 4: In the long run, 95% of sample proportions fall in between 0.2689 and 0.4811.
🔗
  • Valid
  • Incorrect. This confuses the confidence interval for the parameter with the distribution of sample proportions. The confidence interval tells us about plausible values for the parameter, not where sample proportions fall.
  • Invalid
  • Correct! This confuses the confidence interval for the parameter with the distribution of sample proportions. The confidence interval tells us about plausible values for the parameter, not where sample proportions fall.
🔗

Checkpoint 3.3.31.

Statement 5: If the null hypothesis is true, there is a 95% chance the interval contains the parameter.
🔗
  • Valid
  • Incorrect. Confidence intervals don’t depend on whether a null hypothesis is true or not. The confidence level comes from the sampling distribution, not from any hypothesis.
  • Invalid
  • Correct! Confidence intervals don’t depend on whether a null hypothesis is true or not. The confidence level comes from the sampling distribution, not from any hypothesis.
🔗

Checkpoint 3.3.32.

Statement 6: I am 95% confident that Muffin chases the blue ball between 27% and 48% of the time.
🔗
  • Valid
  • Correct! This correctly expresses confidence about the parameter (the underlying probability/long-run proportion). This is a proper interpretation of a confidence interval.
  • Invalid
  • Incorrect. This is actually a valid interpretation because it correctly expresses confidence about the parameter (the underlying probability/long-run proportion).
🔗
🔗
You have attempted of activities on this page.
🔗
PrevTopNext