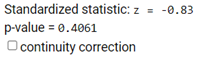Investigation 1.8: Halloween Treat Choices

Section 3.2 Investigation 1.8: Halloween Treat Choices

Obesity has become a widespread health concern, especially in children. Researchers believe that giving children easy access to food increases their likelihood of consuming extra calories.

🔗

Schwartz, Chen, and Brownell (2003) examined whether children would be willing to take a small toy instead of candy at when trick-or-treating on Halloween. They had seven homes in 5 different towns in Connecticut present children with a plate of 4 toys (stretch pumpkin men, large glow-in-the-dark insects, Halloween theme stickers, and Halloween theme pencils) and a plate of 4 different name brand candies (lollipops, fruit-flavored chewy candies, fruit-flavored crunchy wafers, and "sweet and tart" hard candies) to see whether children were more likely to choose the candy or the toy. The houses alternated whether the toys were on the left or on the right. Data were recorded for 284 children between the ages of 3 and 14 (who did not ask for both types of treats).

🔗

Checkpoint 3.2.1. Identify Sample and Variable.

Identify the sample/random process and variable of interest. Which outcome do you want to consider "success"?

🔗

Sample/random process:

🔗

Variable:

🔗

Success:

🔗

Hint.

Think about what is being randomly determined in this study - the choice each child makes when presented with toys and candy.

🔗

Solution.

Sample/random process: The 284 children who were trick-or-treating and presented with a choice between toys and candy.

🔗

Variable: Whether the child chose a toy or candy (categorical).

🔗

Success: Choosing a toy (or choosing candy - either can be defined as success).

🔗

Checkpoint 3.2.2. Define Parameter.

Define (in words) the parameter of interest in this study.

🔗

Hint.

What long-run proportion are we interested in learning about?

🔗

Solution.

The parameter of interest is the probability (or long-run proportion) that a child, when presented with a choice between toys and candy while trick-or-treating, will choose the toy.

🔗

Checkpoint 3.2.3. State Hypotheses.

State an appropriate null and alternative hypothesis involving this parameter (in symbols and in words), for testing whether there is strong evidence of a preference for either the toys or the candy.

🔗

\(H_0: \)

🔗

\(H_a: \)

🔗

Hint.

If there is no preference, what would you expect the probability to be? What would indicate a preference?

🔗

Solution.

\(H_0: \pi = 0.5\text{.}\) The probability that a child chooses a toy is 0.5 (no preference).

🔗

\(H_a: \pi \neq 0.5\text{.}\) The probability that a child chooses a toy is not 0.5 (there is a preference).

🔗

Checkpoint 3.2.4. Predict Distribution.

What does "theory" predict for the mean and standard deviation of the distribution of "number of successes" under the null hypothesis if we model this experiment as a binomial process? Do you expect this distribution to be symmetric and "filled in" or skewed and "gappy"?

🔗

Hint.

For a binomial distribution, the mean is \(n\pi\) and the standard deviation is \(\sqrt{n\pi(1-\pi)}\text{.}\)

🔗

Solution.

Under the null hypothesis with \(n = 284\) and \(\pi = 0.5\text{:}\)

🔗

Mean: \(n\pi = 284(0.5) = 142\)

🔗

Standard deviation: \(\sqrt{n\pi(1-\pi)} = \sqrt{284(0.5)(0.5)} = \sqrt{71} \approx 8.43\)

🔗

Because the sample size is large and \(\pi = 0.5\text{,}\) we expect the distribution to be symmetric and "filled in" (approximately normal).

🔗

Binomial distribution showing approximately normal shape with mean 142 and standard deviation 8.43

🔗

The normal distribution has many, many applications to quantitative variables in general (e.g., many biological variables like height are assumed to follow a normal distribution). For now, we will focus on using this mathematical model as an approximation to the null distribution.

🔗

Central Limit Theorem.

If the sample size is large enough, then the distribution of "number of successes" for a binomial random variable will be well-modeled by the normal probability distribution. The sample size is considered large enough if \(n\times\pi\geq 10\) and \(n\times(1-\pi)\geq 10\text{.}\)

🔗

Checkpoint 3.2.5. Process Probability and Sample Size.

Why does the value of the process probability (\(\pi\)) matter when we check this condition?

🔗

Hint.

Think about what happens when \(\pi\) is very close to 0 or 1.

🔗

Solution.

When \(\pi\) is close to 0 or 1, the binomial distribution becomes more skewed. We need both \(n\pi\) and \(n(1-\pi)\) to be large enough to ensure the distribution is symmetric enough to be well-approximated by a normal distribution. If \(\pi\) is very small, even with a large \(n\text{,}\) we might not have enough expected successes for the normal approximation to work well.

🔗

Checkpoint 3.2.6. Check Validity Conditions.

Does the Central Limit Theorem appear applicable for the Halloween study?

🔗

Hint.

Check both conditions: \(n\pi \geq 10\) and \(n(1-\pi) \geq 10\text{.}\)

🔗

Solution.

Yes, the Central Limit Theorem is applicable.

🔗

\(n\pi = 284(0.5) = 142 \geq 10\) ✓

🔗

\(n(1-\pi) = 284(0.5) = 142 \geq 10\) ✓

🔗

Both conditions are satisfied.

🔗

Checkpoint 3.2.7. Verify with Applet.

Use the One Proportion Inference applet to verify your answers to Checkpoint 3.2.4. Check the Normal Approximation box to verify your answer to Checkpoint 3.2.6.

🔗

Solution.

The mean is at 142 and the standard deviation is at 8.43. The normal distribution overlay matches up pretty well with the binomial distribution though we do see some spaces between the bars.

🔗

One Proportion Inference applet showing binomial distribution with normal approximation overlay

🔗

There are actually some nice advantages to using the normal distribution rather than the binomial distribution, though less so as computers have become so advanced. For one, tail probabilities can be approximated by finding the area under the normal curve rather than summing binomial probabilities.

🔗

Finding a p-value with the normal approximation.

🔗

Checkpoint 3.2.8. Find p-values.

In the sample, 135 children chose the toy and 149 chose the candy. Use the applet to find the following two-sided p-values, and explain briefly how each is found:

🔗

Simulation:

🔗

Exact binomial:

🔗

Normal approximation:

🔗

Hint.

Use the One Proportion Inference applet with \(n = 284\) and \(\pi = 0.5\text{.}\)

🔗

Solution.

With 135 children choosing the toy (fewer than expected under \(H_0\)):

🔗

Simulation: Approximately 0.40 (will vary) - found by simulating many samples from a binomial distribution and counting the proportion as extreme or more extreme than 135.

🔗

Exact binomial: Approximately 0.40 - found by calculating \(P(X \leq 135) + P(X \geq 149)\) using the binomial distribution.

🔗

Normal approximation: Approximately 0.40 - found by calculating the area under the normal curve below 135 and above 149.

🔗

Comparison of p-values from simulation, exact binomial, and normal approximation methods

🔗

The normal approximation is typically applied to the null distribution of sample proportions rather than sample counts.

🔗

Checkpoint 3.2.9. Switch to Proportions.

Use the radio button to toggle the Choice of Statistic to Proportion of heads. What changes about the null distribution? What is the observed value of the statistic?

🔗

Hint.

Convert the count to a proportion: \(135/284\text{.}\)

🔗

Solution.

When switching to proportions, the null distribution is centered at \(\pi = 0.5\) instead of 142, and the standard deviation becomes \(\sqrt{\pi(1-\pi)/n} = \sqrt{0.5(0.5)/284} \approx 0.0297\) instead of 8.43.

🔗

The observed value of the statistic is \(\hat{p} = 135/284 \approx 0.475\text{.}\)

🔗

Key Result.

When the Central Limit Theorem applies, the distribution of sample proportions is approximately normal with mean equal to \(\pi\) and standard deviation equal to \(SD(\hat{p}) = \sqrt{\pi(1-\pi)/n}\text{.}\)

🔗

When we are using the normal distribution, it is even more common to work with the "standardized statistic" by calculating how many standard deviations the statistic is from the expected value (mean) of the null distribution.

🔗

Checkpoint 3.2.10. Calculate Standardized Statistic.

Standardize the value of the statistic for the Halloween study by comparing to the mean and standard deviation of the distribution of sample proportions. Interpret your result in context.

🔗

Standardized statistic \(z = \frac{\text{observed statistic} - \text{expected value}}{SD \text{ of statistic}} = \)

🔗

Interpretation:

🔗

Hint.

Use the formula: \(z = \frac{\hat{p} - \pi_0}{\sqrt{\pi_0(1-\pi_0)/n}}\)

🔗

Solution.

\(z = \frac{0.475 - 0.5}{\sqrt{0.5(0.5)/284}} = \frac{-0.025}{0.0297} \approx -0.84\)

🔗

Interpretation: The observed sample proportion of 0.475 is 0.84 standard deviations below the expected value of 0.5 under the null hypothesis. This is not particularly unusual.

🔗

(What if we had used the sample count instead?)

🔗

Definition.

The One Proportion z-test calculates the standardized statistic as \(z_0 = \frac{\hat{p} - \pi_0}{\sqrt{\pi_0(1-\pi_0)/n}}\) and uses the standard normal distribution (mean 0, std dev 1) to find the p-value.

🔗

Checkpoint 3.2.11. Interpret Subscript Notation.

What does the "zero" subscript tell you?

🔗

Hint.

The subscript indicates this value is calculated under a specific assumption.

🔗

Solution.

The "zero" subscript indicates that this is the value calculated under the null hypothesis (using \(\pi_0\text{,}\) the hypothesized value of the parameter).

🔗

Key Result.

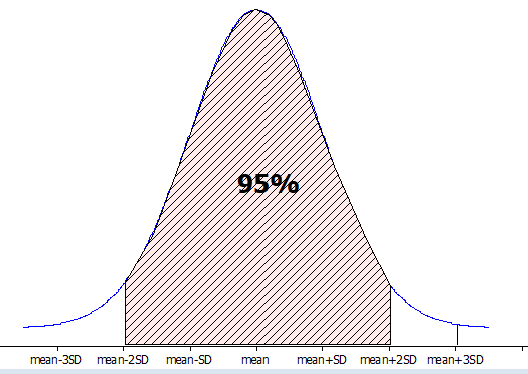
In any normal distribution with mean \(\mu\) and standard deviation \(\sigma\text{,}\) we expect the interval \((\mu - 2\sigma, \mu + 2\sigma)\) to capture approximately 95% of the distribution. In other words, 95% of sample proportions should fall within \(2 \times \sqrt{\pi(1-\pi)/n}\) of \(\pi\text{.}\) So with a normal distribution, the two-standard deviation guideline matches up with a two-sided p-value below 0.05.

🔗

Normal distribution showing middle 95% between -2 and 2 standard deviations

🔗

Checkpoint 3.2.12. Draw Conclusion.

What do you conclude about the plausibility of the null hypothesis based on this standardized statistic?

🔗

Hint.

Is \(|z| > 2\text{?}\)

🔗

Solution.

Since \(|z| = 0.84 < 2\text{,}\) the observed result is within 2 standard deviations of the expected value under the null hypothesis. This suggests the null hypothesis is plausible - we do not have strong evidence against it. The p-value should be greater than 0.05.

🔗

Checkpoint 3.2.13. Calculate p-value from z-statistic.

Use technology to find the corresponding p-value. [Hints: You can calculate the probability from the z-value using standard normal distribution (mean 0, SD 1), e.g., Normal Probability Calculator applet; or use the Technology Detour below to carry out a one-sample z-test.]

🔗

p-value =

🔗

Hint.

For a two-sided test, find \(2P(Z < -0.84)\) or \(2P(Z > 0.84)\text{.}\)

🔗

Solution.

Using technology (Normal Probability Calculator or z-test function), the p-value is approximately 0.40 (or 0.401). This confirms our conclusion that the result is not statistically significant.

🔗

Technology Detour - One Proportion z-test.

Checkpoint 3.2.14. Technology Detour (Theory-Based Inference Applet).

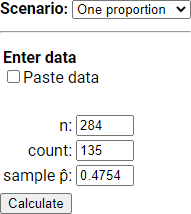
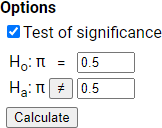
Use the Theory-Based Inference applet to conduct a one proportion z-test:

🔗

Enter the sample size and either the count or the proportion of successes, press Calculate to display sample data.

🔗
Check the box for Test of significance

🔗
Specify the hypothesized value

🔗
Use the button to specify the direction of the alternative.

🔗
Press the Calculate button.

🔗

🔗

Theory-Based Inference applet input screen

Theory-Based Inference applet output screen

Hint.

For the Halloween study, enter n = 284 and either 135 successes or 0.475 as the proportion. Set the hypothesized value to 0.5 and select a two-sided alternative.

🔗

Solution.

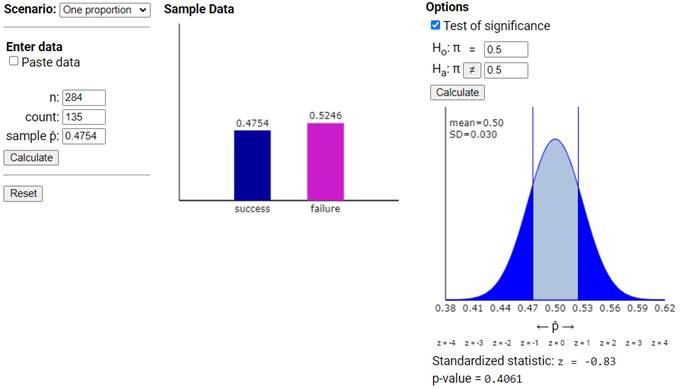
The applet will display:

🔗

Sample statistic: \(\hat{p} = 0.475\)

🔗
Standardized statistic: \(z \approx -0.84\)

🔗
Two-sided p-value: approximately 0.40

🔗
A normal curve with the shaded rejection regions

🔗

🔗

The applet confirms that there is not strong evidence against the null hypothesis that children choose equally between toys and candy.

🔗

Theory-Based Inference applet output for Halloween study showing z-statistic and p-value

🔗

Checkpoint 3.2.15. Technology Detour (R).

Use R to conduct a one proportion z-test. The iscamonepropztest(observed, n, hypothesized, alternative) function takes the following inputs:

🔗

observed = the observation of interest (count or proportion)

🔗
n = the sample size

🔗
hypothesized = the hypothesized process probability (\(\pi\))

🔗
alternative = "below," "above," or "two.sided"

🔗

🔗

Hint.

For the Halloween study, you could use:

🔗

iscamonepropztest(135, 284, 0.5, "two.sided")

🔗

iscamonepropztest(0.475, 284, 0.5, "two.sided")

🔗

Solution.

Running the command:

🔗

library(iscam)
iscamonepropztest(135, 284, 0.5, "two.sided")

Should produce output including:

🔗

Sample proportion: 0.4754

🔗
z-statistic: -0.84

🔗
Two-sided p-value: 0.40

🔗

🔗

The function will also display a graph showing the standard normal distribution with the test statistic and shaded p-value region.

🔗

R output showing one proportion z-test results with standard normal curve and shaded p-value regions

🔗

Checkpoint 3.2.16. Technology Detour (JMP).

Using the ISCAM Journal file in JMP, select Hypothesis Test for One Proportion:

🔗

Use Raw Data or Summary Stats

🔗
Remember to specify a direction for the alternative, a hypothesized proportion, and a significance level (e.g., .05)

🔗

🔗

Hint.

For the Halloween study:

🔗

Select Summary Stats

🔗
Enter n = 284, number of successes = 135

🔗
Hypothesized proportion = 0.5

🔗
Select "not equal" for two-sided test

🔗
Significance level = 0.05

🔗

🔗

Solution.

JMP will display a comprehensive output including:

🔗

Sample proportion: 0.475

🔗
Standard error: 0.0297

🔗
z-statistic: -0.84

🔗
Two-sided p-value: 0.40

🔗
A visual representation of the test

🔗

🔗

The output will indicate that we fail to reject the null hypothesis at the 0.05 significance level.

🔗

JMP output showing one proportion z-test results with test statistics and visual representation

🔗

Checkpoint 3.2.17. Interpret p-value.

Provide a one sentence interpretation of this p-value in context.

🔗

Hint.

What does the p-value tell you about how unusual the observed result would be if the null hypothesis were true?

🔗

Solution.

If children were equally likely to choose toys or candy, we would observe a result as extreme as or more extreme than 135 out of 284 children choosing toys in about 40% of samples.

🔗

Checkpoint 3.2.18. Evaluate Research Implications.

Do you think the researchers are pleased by the lack of significance in this test? Explain, in the context of the study, why such a result might be good news for them.

🔗

Hint.

Consider what the researchers were hoping to demonstrate about offering toys as an alternative to candy.

🔗

Solution.

Yes, the researchers should be pleased! The lack of significance means there’s no strong evidence that children prefer candy over toys. This is good news because it suggests that offering toys as an alternative to candy is viable - children are willing to accept toys instead of candy. If there had been strong evidence of a preference for candy, it would suggest that offering toys wouldn’t be an effective strategy to reduce candy consumption.

🔗

Improving the normal approximation.

Even though we passed the "validity conditions" for the normal approximation for this study, we could still use a "continuity correction" to improve the approximation.

🔗

Checkpoint 3.2.19. Compare p-values.

Which p-value from the earlier comparison (exact binomial or normal approximation) is closer to your simulated p-value? Is this expected?

🔗

Hint.

The exact binomial should match the simulation closely.

🔗

Solution.

The exact binomial p-value should be closer to the simulated p-value. This is expected because the simulation approximates the true binomial distribution, while the normal approximation is just that - an approximation to the binomial.

🔗

Checkpoint 3.2.20. Compare Discrete and Continuous.

In the binomial distribution \(P(X = 135) = 0.220\text{.}\) What is \(P(X = 135)\) with the normal distribution? How do \(P(X < 135)\) and \(P(X \leq 135)\) compare in each distribution?

🔗

Hint.

For a continuous distribution, the probability of any exact value is 0.

🔗

Solution.

With the normal distribution (continuous), \(P(X = 135) = 0\) because the probability of any exact value is 0 for a continuous distribution.

🔗

In the binomial distribution (discrete): \(P(X \leq 135) = P(X < 135) + P(X = 135)\text{,}\) so these are different values.

🔗

In the normal distribution (continuous): \(P(X \leq 135) = P(X < 135)\) because \(P(X = 135) = 0\text{.}\)

🔗

To make the normal probability (which is finding \(P(X < 135)\)) closer to the binomial probability, which finds \(P(X \leq 135) = P(X < 135) + P(X = 135)\text{,}\) we want to include more of the area under the normal curve above 135 in our calculation. A continuity correction does this by using the normal distribution to find \(P(X < 135.5)\) instead. This does not change the binomial probability but should enlarge the normal probability.

🔗

Checkpoint 3.2.21. Apply Continuity Correction.

In the One Proportion Inference applet, specify 135.5 in the As Extreme As box (if using number of successes as the statistic, otherwise use \(135.5/284 \approx 0.477\) instead) and press Count. What does the applet use for the right-side cut-off? Why? How does the p-value change? Is it now more similar to the binomial p-value?

🔗

Hint.

By symmetry, what value on the right side corresponds to 135.5 on the left side?

🔗

Solution.

The applet uses 148.5 for the right-side cut-off. This is because 135.5 is 6.5 below the mean of 142, so by symmetry, we need 6.5 above the mean: \(142 + 6.5 = 148.5\text{.}\)

🔗

The p-value should increase slightly (become closer to 0.40) and should now be more similar to the exact binomial p-value. The continuity correction improves the normal approximation by accounting for the fact that the normal distribution is continuous while the binomial is discrete.

🔗

Many software programs allow you to apply this continuity correction for a one-sample z-test (e.g., using \(\hat{p} = (X \pm 0.5)/n\) as the input) or may do so by default. However, when n is large, you may not see much difference in the values.

🔗

Technology Detour - Continuity Correction.

Checkpoint 3.2.22. Technology Detour (Theory-Based Inference Applet).

Use the Theory-Based Inference applet to apply a continuity correction:

🔗

Check the continuity correction box to apply the continuity correction to the standardized statistic and p-value.

🔗

🔗

Theory-Based Inference applet with continuity correction option

Hint.

For the Halloween study, after entering the data (n = 284, 135 successes), check the continuity correction box and observe how the p-value changes.

🔗

Solution.

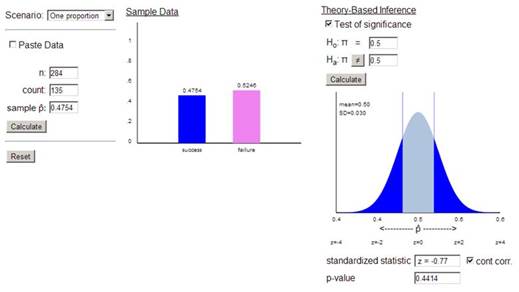
With the continuity correction applied:

🔗

The p-value changes from approximately 0.4061 to 0.4382

🔗
This is much closer to the exact binomial p-value of 0.4405

🔗
The continuity correction adjusts for the fact that we’re using a continuous distribution (normal) to approximate a discrete distribution (binomial)

🔗

🔗

Theory-Based Inference applet showing continuity correction applied to Halloween study

🔗

Checkpoint 3.2.23. Technology Detour (R).

The iscambinomnorm(k, n, prob, direction) function gives a visual of the continuity correction. It takes the following inputs:

🔗

k = the observation of interest

🔗
n = the sample size

🔗
prob = the process probability (\(\pi\))

🔗
direction = "below," "above," or "two.sided"

🔗

🔗

Hint.

For the Halloween study, try:

🔗

iscambinomnorm(135, 284, 0.5, "two.sided")

🔗

Solution.

Running the command:

🔗

library(iscam)
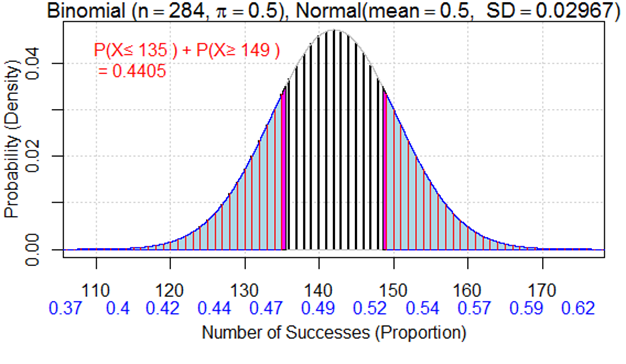
iscambinomnorm(135, 284, 0.5, "two.sided")

This function creates a graph showing:

🔗

The binomial distribution (bars)

🔗
The normal approximation (curve)

🔗
The continuity correction boundaries at 135.5 and 148.5

🔗
The corrected p-value of approximately 0.4382

🔗

🔗

The visualization clearly shows how the continuity correction includes more area under the normal curve to better match the binomial probabilities.

🔗

R visualization showing continuity correction comparison

🔗

Study Conclusions.

If we define \(\pi\) to be the probability that, when presented with a choice of candy or a toy while trick-or-treating, a child chooses the toy, and if we assume the null hypothesis (\(H_0: \pi = 0.5\)) is true, the above calculations tell us that we would observe at most 135 children choosing candy (or at least 149 choosing toy) or at most 135 of the 284 children choosing the toy in about 40% of all possible samples from such a process. Thus, this is not a surprising outcome when \(\pi = 0.5\text{.}\) We fail to reject the null hypothesis and conclude that it’s plausible that children are equally likely to choose the toy or the candy.

🔗

We do have some cautions with this study as it was conducted in only a few households in Connecticut, a "convenience sample," so we cannot claim that these results are representative of children in other neighborhoods. We also don’t know if the children found the toys "novel" and whether their preference for toys could decrease as the novelty wears off (or if "better" candy choices were offered). Furthermore, when the children approached the door they were asked their age and gender, and for a description of their Halloween costume. The researchers caution that this may have cued the children that their behavior was being observed (even though their responses were recorded by another research member who was out of sight) or that they should behave a certain way. Still, these researchers were optimistic that alternatives could be presented to children, even at Halloween, to lessen their exposure to large amounts of candy.

🔗

Subsection 3.2.1 Practice Problem 1.8A

In Investigation 1.6, Dr. Güntürkün conjectured that 2/3 of kissing couples lean right.

🔗

Checkpoint 3.2.24. Normal Approximation Validity.

Would the normal approximation (Central Limit Theorem) be valid for the kissing study in Investigation 1.6? Justify your answer.

🔗

Checkpoint 3.2.25. z-test and p-value.

Dr. Güntürkün found 80 out of 124 couples leaned right in his sample. Find the one-proportion z-test statistic and normal-based two-sided p-value. Do the standardized statistic and p-value agree? How does the normal-based p-value compare to the exact binomial p-value for this study?

🔗

Checkpoint 3.2.26. Continuity Correction.

Repeat the previous calculation using the continuity correction and compare the results.

🔗

Subsection 3.2.2 Practice Problem 1.8B

A student wanted to assess whether her dog Muffin tends to chase her blue ball and her red ball equally often when they are rolled at the same time. The student rolled both balls a total of 96 times, each time keeping track of which ball Muffin chased. The student found that Muffin chased the blue ball 52 times and the red ball 44 times. Let’s treat the blue ball as "success."

🔗

Checkpoint 3.2.27. State Hypotheses.

State the appropriate null and alternative hypotheses in symbols. (Be sure to describe what the symbol represents in this context.)

🔗

Checkpoint 3.2.28. Calculate Test Statistic.

Report and interpret the values of the z-test statistic and normal-based p-value using a continuity correction.

🔗

Checkpoint 3.2.29. Conclusion.

Summarize your conclusion about the student’s question concerning her dog Muffin.

🔗

Checkpoint 3.2.30. Explain Reasoning.

Explain the reasoning process behind your conclusion.

🔗

Checkpoint 3.2.31. Alternate Definition.

How would your answers to the previous questions change if we had used the red ball as success?

🔗

You have attempted of activities on this page.

🔗

Prev Top Next